
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка поведения цепей Маркова при большом числе шаговСодержание книги
Поиск на нашем сайте
В этом параграфе рассмотрен класс задач, связанных с оценкой предельных вероятностей пребывания системы в состояниях эргодического множества. Как было выяснено выше, динамика смены состояний однородной цепи Маркова определяется поведением матрицы Для оценки скорости сходимости можно привести матрицу
где
а матрица Напомним, что i -е собственное число матрицы
а собственный вектор
Преобразование (1.13) удобно тем, что при возведении в степень матрицы
причем
Таким образом, динамику изменения матрицы Мы уже упоминали, что матрица Возможен еще один способ нахождения предельных вероятностей. Исходя из того, что Пример. В качестве примера исследования поведения цепи Маркова при большом числе шагов рассмотрим систему с двумя состояниями
с начальным распределением вероятностей Требуется найти предельное распределение вероятностей нахождения в состояниях Задачу решим тремя разными способами. 1. Путем численного возведения матрицы
2. Путем спектрального разложения матрицы Найдем собственные числа матрицы
откуда Определим собственные векторы По формуле (3.15) для
Полученное уравнение не доопределено, поэтому, приняв Аналогично для
Следовательно, матрица а обратная к ней матрица Таким образом, спектральное представление матрицы P имеет вид
Теперь можно вычислить предельное распределение вероятностей:
что совпадает с результатами предыдущих вычислений. 3. Исходя из того, что Получаем систему уравнений:
Решая эту систему (в ней одно уравнение лишнее), получим уже знакомый ответ
|
|||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 51; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.1.58 (0.006 с.) |

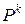 при
при  . Однако непосредственное применение формулы (1.2) для определения переходных характеристик этого процесса, в частности, скорости сходимости к предельным вероятностям пребывания в различных состояниях при
. Однако непосредственное применение формулы (1.2) для определения переходных характеристик этого процесса, в частности, скорости сходимости к предельным вероятностям пребывания в различных состояниях при 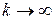 , не всегда удобно.
, не всегда удобно.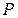 к диагональному виду с помощью линейного преобразования. Предположим, что матрица
к диагональному виду с помощью линейного преобразования. Предположим, что матрица 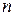 собственных чисел
собственных чисел 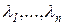 . Тогда ее можно привести к виду
. Тогда ее можно привести к виду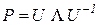 , (1.13)
, (1.13)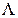 - диагональная матрица
- диагональная матрица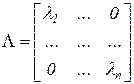 ,
,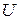 составлена из собственных векторов матрицы
составлена из собственных векторов матрицы 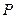 при собственном числе
при собственном числе 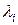 .
.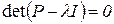 , (1.14)
, (1.14)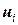 , соответствующий собственному числу
, соответствующий собственному числу 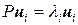 . (1.15)
. (1.15)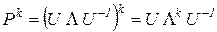 , (1.16)
, (1.16)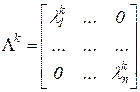 . (1.17)
. (1.17)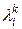 ,
, 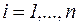 .
.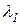 равно 1, и ему соответствует собственный вектор, составленный из единиц:
равно 1, и ему соответствует собственный вектор, составленный из единиц: 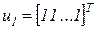 .
.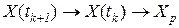 при
при 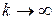 , уравнение (1.4) можно записать в виде
, уравнение (1.4) можно записать в виде 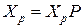 , добавив условие
, добавив условие  , а затем решить полученную систему уравнений.
, а затем решить полученную систему уравнений.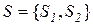 , описываемую матрицей
, описываемую матрицей ,
,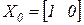 .
.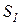 ,
, 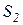 при большом числе шагов
при большом числе шагов 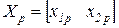 .
.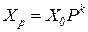 ,
,  , например,
, например, 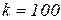 . Проделав вычисления, получим
. Проделав вычисления, получим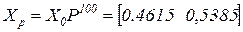 .
.
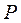 по формуле (1.14):
по формуле (1.14):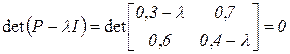 ,
,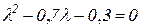 ,
, 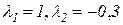 ,
, 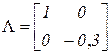 .
.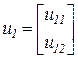 ,
, 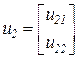 .
.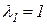 .
.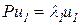 ,
, 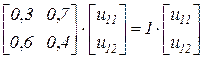 .
.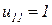 , получим
, получим 
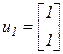 .
.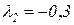 имеем уравнение
имеем уравнение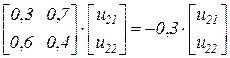 , и, приняв
, и, приняв  , получим
, получим 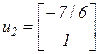 .
.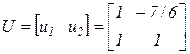 ,
,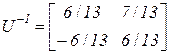 .
.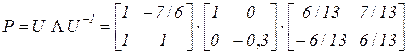 .
.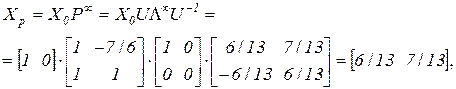
 при
при 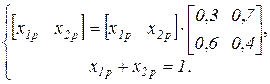
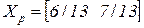 .
.


