
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение и динамика цепи Маркова
Рассмотрим систему å, находящуюся в каждый из дискретных моментов Система рассматривается в моменты времени, образующие множество
Каждый элемент матрицы
Причем (и это основное свойство марковских процессов) вероятность перехода из Понятно, что переходы во все возможные состояния (в том числе в себя) образуют полную группу событий, поэтому Пусть вектор-строка
где Нетрудно видеть, что правая часть написанной формулы определяет произведение вектора
Последовательность состояний В этом случае рекуррентная формула (3.4) может быть записана в виде
…·
где Нетрудно убедиться, что сумма вероятностей нахождения системы во всех состояниях (т.е. сумма элементов вектора Последовательность векторов Отметим, что матрицы P, порождающие цепи Маркова, т.е. такие, у которых все элементы
Рассмотрим классификацию состояний цепи Маркова. Множество всех состояний может быть разбито на непересекающиеся подмножества, или классы: невозвратные и эргодические. Их свойства определяются следующим образом. Если процесс покинул класс состояний первого типа, он никогда в него не возвращается. Если процесс попал в класс состояний второго типа, то он никогда его не покидает. Невозвратное множество мы будем обозначать Для цепи Маркова с
где
Матрица Q размерности Матрица R размерности Матрица Поскольку из множества При возведении матрицы P в степень перемножаются блоки, указанные в (1.9), и произвольная степень канонической матрицы имеет вид
1.1.2 Оценка длительности пребывания процесса Рассмотрим поведение цепи Маркова при росте числа шагов k. Из анализа структуры матрицы
При моделировании реальных систем с помощью конечных цепей Маркова часто бывает необходимо оценивать показатели продолжительности работы системы или трудоемкости процессов. Для этой цели нужно уметь рассчитывать число шагов, в течение которых процесс не покидает множество Обозначим - вычисление математического ожидания величин - вычисление дисперсий Переходя к вычислению матожидания величины Для дальнейшего нам понадобится формула, оценивающая матрицу
Поскольку при Матрица Следовательно, существует обратная матрица
Перейдем теперь к оценке среднего «время жизни» состояний процесса, относящихся к невозвратному множеству. Обозначим как и прежде через Можно показать, что матрица математических ожиданий чисел Для того, чтобы в этом убедиться, введем вспомогательную переменную (индикатор)
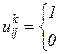
Вероятность того, что Легко видеть, что Оценим теперь матожидание матрицы, образованной элементами
Здесь Таким образом, среднее число шагов, которое проводит процесс в невозвратном состоянии,
Отсюда следует, что матрица математических ожиданий числа пребываний системы в невозвратных состояниях равна фундаментальной матрице цепи Маркова:
где I – единичная матрица. Каждый элемент Зная
где - В ряде случаев исследователя может интересовать оценка дисперсии трудоемкости процесса. Для этой цели вычисляется матрица дисперсий числа пребываний процесса в множестве невозвратных состояний по формуле, которую мы приводим без вывода:
где индексы
|
|||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 41; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.31.73 (0.023 с.) |
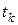 в одном из
в одном из 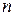 состояний
состояний 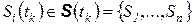 .
.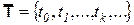 . В каждый момент времени система может находиться только в одном из состояний. Состояния изменяются со временем случайным образом. Это изменение определяется матрицей переходных вероятностей
. В каждый момент времени система может находиться только в одном из состояний. Состояния изменяются со временем случайным образом. Это изменение определяется матрицей переходных вероятностей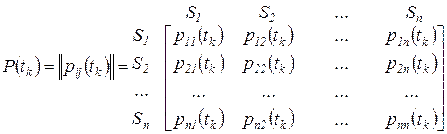 . (1.1)
. (1.1)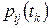 определяет вероятность того, что если å в момент
определяет вероятность того, что если å в момент 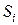 , то в момент
, то в момент  она окажется в состоянии
она окажется в состоянии 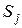 :
: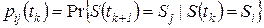 (1.2)
(1.2)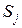 не зависит от предыдущих состояний.
не зависит от предыдущих состояний.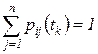 для всех
для всех 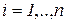 ,
, 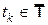 .
.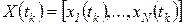 - описывает распределение вероятностей нахождения å в соответствующих состояниях в момент
- описывает распределение вероятностей нахождения å в соответствующих состояниях в момент 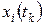 - это вероятность того, что в момент
- это вероятность того, что в момент 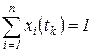 ,
, 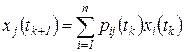 (1.3)
(1.3)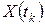 на матрицу
на матрицу 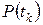 и в векторной форме эквивалентна следующей записи динамического процесса:
и в векторной форме эквивалентна следующей записи динамического процесса: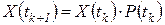 . (1.4)
. (1.4)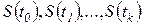 называется конечной цепью Маркова. Цепь называется однородной, если
называется конечной цепью Маркова. Цепь называется однородной, если 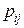 не зависит от времени.
не зависит от времени. ,
,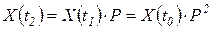 ,
,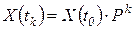 , (1.5)
, (1.5)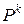 - k -я степень матрицы P.
- k -я степень матрицы P.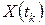 ,
, 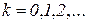 определяет динамику моделируемого процесса.
определяет динамику моделируемого процесса.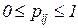 , а их суммы по столбцам равны единице для всех строк:
, а их суммы по столбцам равны единице для всех строк: 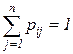 ,
,  , называют стохастическими.
, называют стохастическими.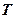 , а эргодическое -
, а эргодическое - 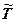 . При этом
. При этом 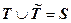 ,
, 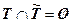 . Если эргодическое множество содержит только одно состояние, то это состояние называется поглощающим. Для такого состояния
. Если эргодическое множество содержит только одно состояние, то это состояние называется поглощающим. Для такого состояния 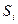 элемент переходной матрицы
элемент переходной матрицы 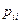 должен быть равен 1, следовательно, все остальные элементы соответствующей строки равны 0. Цепь, все эргодические состояния которой являются поглощающими, называется поглощающей цепью.
должен быть равен 1, следовательно, все остальные элементы соответствующей строки равны 0. Цепь, все эргодические состояния которой являются поглощающими, называется поглощающей цепью.
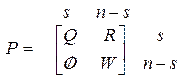 (1.6)
(1.6)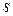 - количество состояний в невозвратном множестве;
- количество состояний в невозвратном множестве;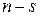 - количество состояний в эргодическом множестве.
- количество состояний в эргодическом множестве.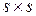 определяет поведение процесса до выхода из множества невозвратных состояний.
определяет поведение процесса до выхода из множества невозвратных состояний.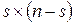 определяет вероятности перехода из множества невозвратных состояний в эргодическое множество.
определяет вероятности перехода из множества невозвратных состояний в эргодическое множество.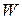 размерности
размерности 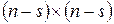 определяет динамику эргодических состояний.
определяет динамику эргодических состояний.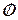 размерности
размерности 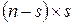 состоит из нулей.
состоит из нулей.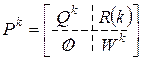 (1.7)
(1.7)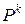 (1.7) следует, что процесс, стартовав из некоторого состояния
(1.7) следует, что процесс, стартовав из некоторого состояния 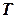 , на каждом шаге с вероятностями, определенными матрицей
, на каждом шаге с вероятностями, определенными матрицей 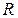 , переходит в эргодическое множество
, переходит в эргодическое множество 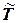 . Через определенное число шагов процесс окажется в
. Через определенное число шагов процесс окажется в 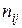 общее число моментов времени (тактов работы системы), проведенных процессом в состоянии
общее число моментов времени (тактов работы системы), проведенных процессом в состоянии 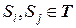 ). Понятно, что
). Понятно, что 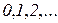 с соответствующими вероятностями, которые мы будем обозначать
с соответствующими вероятностями, которые мы будем обозначать 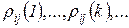 . Таким образом,
. Таким образом, 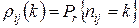 - вероятность того, что система за все «время жизни» процесса находилась в состоянии
- вероятность того, что система за все «время жизни» процесса находилась в состоянии  раз. При этом
раз. При этом 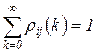 . Зная распределение вероятностей
. Зная распределение вероятностей 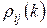 , можно вычислить все необходимые статистические характеристики процесса – математическое ожидание, дисперсию и другие. Однако вычисление таких распределений в общем случае – достаточно сложная задача, поэтому мы ограничимся в данном разделе рассмотрением двух более простых практически важных задач:
, можно вычислить все необходимые статистические характеристики процесса – математическое ожидание, дисперсию и другие. Однако вычисление таких распределений в общем случае – достаточно сложная задача, поэтому мы ограничимся в данном разделе рассмотрением двух более простых практически важных задач: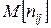 и средних значений трудоемкости процесса;
и средних значений трудоемкости процесса;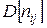 и среднеквадратичных отклонений трудоемкости процесса.
и среднеквадратичных отклонений трудоемкости процесса.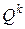 , входящей в структуру
, входящей в структуру 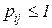 , и
, и 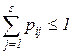 (в отличие от матрицы
(в отличие от матрицы 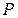 , для которой
, для которой 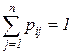
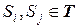 , то при больших
, то при больших  при
при 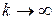 . Здесь
. Здесь 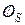 - нулевая квадратная матрица s -го порядка.
- нулевая квадратная матрица s -го порядка.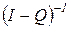 . Рассмотрим тождество
. Рассмотрим тождество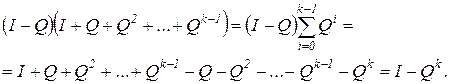
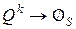 , то
, то 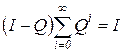 .
.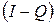 неособенная, т.к.
неособенная, т.к. 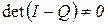 , в чем легко убедиться.
, в чем легко убедиться.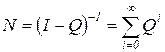 . (1.8)
. (1.8)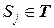 .
.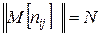 , где
, где 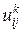 , которая принимает единичное значение, если процесс, стартовав при
, которая принимает единичное значение, если процесс, стартовав при 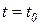 из
из 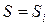 оказывается при
оказывается при 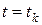 в
в 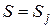 , т.е.
, т.е.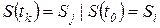 ,
в противном случае.
,
в противном случае.
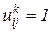 , обозначим
, обозначим 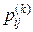 .
.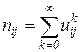 .
.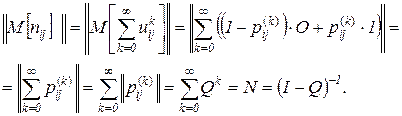
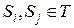 .
.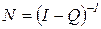 , (1.10)
, (1.10) представляет собой среднее число пребываний процесса в состоянии Sj при старте из состояния
представляет собой среднее число пребываний процесса в состоянии Sj при старте из состояния 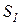 , достаточно рассматривать только первую строку матрицы
, достаточно рассматривать только первую строку матрицы 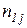 , можно вычислить среднюю трудоемкость процесса по формуле
, можно вычислить среднюю трудоемкость процесса по формуле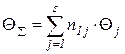 , (1.11)
, (1.11)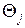 трудоемкость j – го шага процесса в соответствующих единицах.
трудоемкость j – го шага процесса в соответствующих единицах.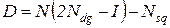 , (1.12)
, (1.12)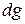 и
и  обозначают соответственно выделение диагональных элементов матрицы
обозначают соответственно выделение диагональных элементов матрицы 


