
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раскрашенные (цветные) сети Петри (CPN)Содержание книги
Поиск на нашем сайте
Определение раскрашенных (цветные) сети Петри (C PN) В последние годы широко используется методология моделирования дискретных систем, основанная на использовании раскрашенных (цветных) сетей Петри – Coloured Petri Net (CPN). Эта методология является обобщением формализма обыкновенных сетей Петри на случай многих видов ресурсов и позволяет более эффективно моделировать сложные системы. На базе методологии CPN разработан специальный язык моделирования – Coloured Petri Net Modelling Language (CPN ML) и созданы соответствующие программные средства. Правила функционирования CPN сложнее правил для обыкновенных сетей Петри. В то же время, структура сети – двудольный ориентированный мультиграф, и основной шаг работы – изменение маркировок при срабатывании переходов – принципиально не различаются. Ниже рассмотрено несколько упрощенное и по возможности нефор-мализованное описание CPN ориентированное на синтаксис языка Паскаль. Полное и строгое описание CPN содержится в книге Курта Йенсена [5].
Мультимножества Одним из важных понятий, используемых в теории раскрашенных сетей Петри, является понятие мультимножества. Формально мультимножеством Иными словами, мультимножество
где Пример. Пусть Рассмотрим операции над мультимножествами. 1. Сложение мультимножеств. Пусть Тогда 2. Умножение мультимножества на скаляр. Пусть Тогда 3. Сравнение мультимножеств. Мы будем говорить, что если 4. Вычитание мультимножеств. если
5. Мощность мультимножества – суммарное число элементов в мультимножестве:
Формальное определение CPN раскрашенная сеть Петри CPN – это кортеж
Рассмотрим элементы определения (3.1). 1. var teta: Integer;. 2.
При описании переменных, используемых в сети, указывают их принадлежность к типу, например:
В последнем примере переменная 3.
а для работы с ним вводится переменная
С каждой позицией может быть связана определенная маркировка, которая учитывает наличие различных типов ресурсов. Маркировка позиции
Здесь Совокупность маркировок всех позиций называется маркировкой сети:
В языке Паскаль мультимножество, определяющее маркировку позиции, может быть представлено, например, типом – множество, состоящим из записей вида
Операции над мультимножествами можно определить соответствующими процедурами. Аналогично определяется мультимножество, задающее маркировку сети. 4.
и соответствующей переменной:
Это множество не отличается от множества переходов для обыкновенных сетей Петри, однако правила их срабатывания могут быть более сложными. Эти правила рассмотрены ниже. 5. В этих выражениях первый элемент указывает начало дуги, второй элемент – конец дуги. множество
где дуги
Поскольку дуги имеют два вида: от позиции к переходу (
где множество Как и в случае обыкновенных сетей Петри, элементы множеств
6.
Рассмотрим один из способов задания этой функции. Каждая дуга может быть представлена в виде записи. Дуги типа
Дуги типа
Множества дуг
Для работы с дугами вводятся переменные соответствующих типов:
7.
означает, что цвета типа 8.
принимает истинное значение для перехода 9. Рассмотрим примеры задания функции
- дуга
- дуга
- дуга
- дуга Отсутствие выражения для какой-либо дуги означает, что дуга не помечена. 9. Например, Функционирование CPN Рассмотрим работу раскрашенных сетей Петри. Как и в случае обыкновенных СП, функционирование сети состоит в срабатывании переходов и происходящих вследствие этого изменениях маркировок. Мы будем говорить, что переход
В первой скобке выражения (4.20) происходит поэлементное сравнение мультимножества, являющегося маркировкой позиции Суммирование мультимножеств Во второй скобке записано условие отсутствия блокировки перехода Если условие срабатывания перехода Изменение маркировки узла
В выражении (4.21) все слагаемые являются мультимножествами, и вычисления производятся в соответствии с правилами сложения и вычитания мультимножеств. Знаки суммирования мультимножеств используются в формуле по причине, которая уже пояснена выше: каждая пара узлов может быть связана несколькими дугами, а каждая дуга Если на некотором шаге Пример. Приведем описание простой CPN, схема которой и начальная маркировка приведены на рисунке 3.1 а. а) б) Рисунок 3.1 Раскрашенная сеть Петри и
· Множества цветов:
· Переменные:
· Множество позиций:
· Множество переходов:
· Множество дуг
· Цветовая функция
· Блокировочная функция отсутствует:
· функция
· функция инициализации
Ниже приведено полное дерево маркировок рассмотренной сети.
Поясним описание сети. Для позиции В позицию При работе сети переменная Эквивалентная рассмотренной CPN обыкновенная сеть Петри приведена на рисунке 3.1 б. Построив дерево маркировок этой сети, нетрудно убедиться, что оно структурно совпадает с рассмотренным выше деревом CPN. Однако раскрашенная сеть содержит больше информации, поскольку ресурсы в позиции Расширения CPN Как уже отмечалось, использование сетей Петри в различных прикладных задачах может потребовать придания им дополнительных возможностей, что приводит к созданию расширений этих сетей. Некоторые расширения аналогичны рассмотренным в п 2.1.5, (например иерархические CPN), потребность в ряде других отсутствует, т.к. формализм CPN позволяет их описать (CPN с приоритетами, ингибиторные сети, самомодифицируемые сети). Ниже мы рассмотрим одно важное расширение CPN, значительно расширяющее их моделирующие возможности: CPN с временным механизмом Существует ряд задач моделирования, в которых необходимо учитывать не только последовательность событий, но и время их наступления, а также продолжительность. Для этой цели предусмотрено расширение возможностей раскрашенных сетей Петри путем введения временного механизма (так называемых timed CPN [10]). В несколько упрощенном виде сущность такого расширения описана ниже. А. В модель системы вводятся часы, показывающие глобальное время Б. Ресурсы, перемещаемые в сети (фишки) могут получить временные метки. Такие ресурсы, в общем виде, задаются мультимножествами с временными метками (timed multi-sets), однако мы эту теорию не рассматриваем. Отметим лишь, что при описании множества цветов добавляются пометки timed, а переменные соответствующего типа снабжаются знаками @ (по-английски читается at, т.е. «во время»). Это означает, что переменная привязана к глобальному времени. После значка @ в квадратных скобках указывается значение глобального времени, в течение которого возможно использование данных фишек при срабатывании переходов, для которых они являются входными. При этом запись вида @[500] говорит о том, что фишка «включается» в момент Приведем пример.
Возможное значение мультимножества определяемого переменной
В. Каждый переход, на вход которого поступают фишки, имеющие временные метки, получает дополнительное условие срабатывания: он может сработать только в том случае, если системное время удовлетворяет всем условиям на входных фишках. В свою очередь, при срабатывании переход может увеличить временную метку фишки, т.е. смоделировать задержку в работе системы. Величина задержки определяется специальным выражением связанным с переходом, и имеющим вид
Рисунок 3.2 Фрагмент CPN с временными метками Пусть в сети на рисунке 3.2 начальная маркировка такова:
Выражения на дугах показаны на схеме. Глобальное время
3.1.5 Сравнение формализмов обыкновенных и Подведем некоторые итоги данного раздела. Мы кратко рассмотрели теорию сетей Петри в двух вариантах: · формализм классических или обыкновенных СП (РТ – сетей в терминологии К. Йенсена); · формализм раскрашенных сетей Петри - CPN. Нетрудно убедиться в том, что формализм описания структуры и функционирования CPN справедлив и для обыкновенных СП. При этом пункты 1, 3, 4 и 10 совпадают с описанием в разделе 2.1.1; цветовое множество всего одно и имеет единственный цвет; описание связей между узлами вместо матриц Правила срабатывания и изменения маркировок (3.8) и (3.9) при сделанных предположениях совпадают соответственно с (2.6) и (2.7). В то же время, очевидно, что формализм CPN К. Йенсена при всех своих преимуществах в ряде случаев более громоздок и менее удобен по сравнению с формализмом классических обыкновенных сетей Петри. Поэтому при моделировании конкретных систем исследователь должен выбирать наиболее подходящую в данном случае методологию. Именно так мы и будем поступать в дальнейшем.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.01 с.) |

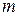 на непустом множестве
на непустом множестве 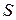 называется функция
называется функция 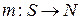 , где
, где  - множество натуральных чисел.
- множество натуральных чисел.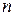 раз (
раз (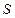 можно представить суммой
можно представить суммой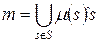
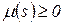 – число появлений (кратность) элемента
– число появлений (кратность) элемента 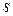 в мультимножестве
в мультимножестве 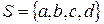 – множество элементов и
– множество элементов и 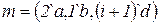 – мультимножество на
– мультимножество на 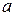 , одного элемента
, одного элемента  , нуля (ни одного) элементов
, нуля (ни одного) элементов  и
и 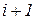 элементов
элементов 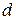 , где
, где  – переменная типа integer.
– переменная типа integer.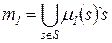 ,
, 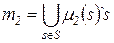 .
.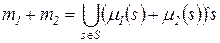 .
. - скаляр типа integer.
- скаляр типа integer. .
.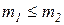 ,
,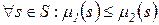 .
.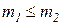 , то можно определить разность мультимножеств:
, то можно определить разность мультимножеств: .
.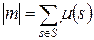 .
. . (3.1)
. (3.1) - множество дискретных моментов времени (шагов), в которые происходит функционирование сети. Номер шага есть переменная целого типа:
- множество дискретных моментов времени (шагов), в которые происходит функционирование сети. Номер шага есть переменная целого типа: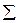 – конечное множество непустых типов, называемое цветами. Типы имеют общее название
– конечное множество непустых типов, называемое цветами. Типы имеют общее название 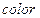 и задаются аналогично тому, как это принято в языках программирования. Например:
и задаются аналогично тому, как это принято в языках программирования. Например: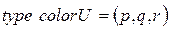 ; – перечисляемый тип, здесь
; – перечисляемый тип, здесь 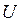 - имя цветного множества,
- имя цветного множества, 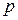 ,
, 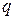 ,
, 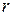 – входящие в него цвета;
– входящие в него цвета; ; – целый тип;
; – целый тип; ; – прямое произведение типов.
; – прямое произведение типов. ;
; 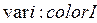 ;
; 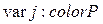 .
.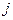 состоит из пары элементов
состоит из пары элементов 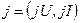 , где элемент
, где элемент  принадлежит типу
принадлежит типу  , а
, а 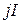 – типу
– типу 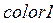 .
.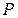 – конечное множество позиций. Это множество может быть представлено перечисляемым типом:
– конечное множество позиций. Это множество может быть представлено перечисляемым типом: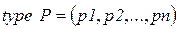 ; (3.2)
; (3.2) .
.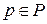 представляет собой мультимножество, например, следующего вида:
представляет собой мультимножество, например, следующего вида: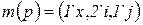 .
. ,
, 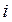 ,
,  - переменные указанных в п. 2 цветовых типов, определяющие различные виды ресурсов, а цифры, стоящие перед кавычками – количество фишек соответствующего типа, в позиции
- переменные указанных в п. 2 цветовых типов, определяющие различные виды ресурсов, а цифры, стоящие перед кавычками – количество фишек соответствующего типа, в позиции 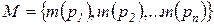 .
.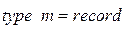 ; (3.3)
; (3.3)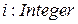 ;
; 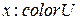 ;
; 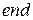 ;.
;.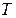 – конечное множество переходов, которое можно представить перечисляемым типом
– конечное множество переходов, которое можно представить перечисляемым типом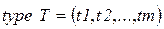 ; (3.4)
; (3.4)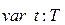 .
. – конечное множество дуг, связывающих между собой позиции и переходы. В отличие от обыкновенных сетей Петри, где дуги задаются матрицами инцидентности
– конечное множество дуг, связывающих между собой позиции и переходы. В отличие от обыкновенных сетей Петри, где дуги задаются матрицами инцидентности 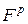 и
и 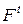 , в языке CPN ML указываются все дуги с помощью выражений вида:
, в языке CPN ML указываются все дуги с помощью выражений вида: 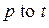 и
и 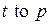 , где
, где 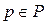 ,
, 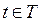 . Такая нотация введена для того, чтобы можно было пару элементов
. Такая нотация введена для того, чтобы можно было пару элементов 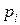 ,
,  соединить несколькими дугами с различными свойствами.
соединить несколькими дугами с различными свойствами.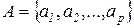 ,
, определяются одним из видов выражений:
определяются одним из видов выражений: или
или 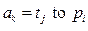 ,
,  ,
, 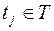 .
.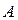 можно представить в виде суммы непересекающихся множеств:
можно представить в виде суммы непересекающихся множеств: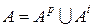 ,
, 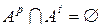 ,
,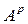 содержит элементы вида
содержит элементы вида 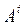 –элементы вида
–элементы вида  .
.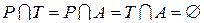 .
.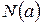 – узловая функция, которая для каждой дуги
– узловая функция, которая для каждой дуги 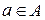 указывает ее исходный и конечный узел. Формально
указывает ее исходный и конечный узел. Формально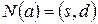 ,
, 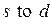 . Здесь
. Здесь 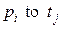 задаются записью
задаются записью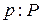 ;
; 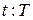 ;
;  задаются аналогично:
задаются аналогично: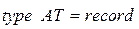 ; (3.6)
; (3.6) и
и 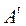 могут быть представлены перечисляемыми типами:
могут быть представлены перечисляемыми типами: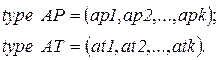 (3.7)
(3.7)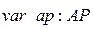 ;
; 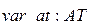 .
. – цветовая функция, определяющая множество типов цветов, разрешенных для каждой позиции. Например, запись
– цветовая функция, определяющая множество типов цветов, разрешенных для каждой позиции. Например, запись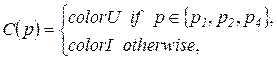
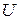 разрешены для позиций
разрешены для позиций 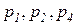 , а цвета типа
, а цвета типа 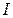 разрешены для всех остальных позиций из
разрешены для всех остальных позиций из 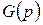 – блокировочная (спусковая) функция, описывающая дополнительные условия, которые должны быть выполнены для срабатывания перехода
– блокировочная (спусковая) функция, описывающая дополнительные условия, которые должны быть выполнены для срабатывания перехода 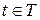 . Эта функция представляет собой предикат, составленный из переменных, принадлежащих типам цветов
. Эта функция представляет собой предикат, составленный из переменных, принадлежащих типам цветов 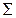 . Например, функция
. Например, функция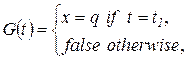
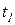 если переменная
если переменная 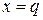 , а во всех остальных случаях она ложь. Таким образом, для того, чтобы было разрешено срабатывание перехода
, а во всех остальных случаях она ложь. Таким образом, для того, чтобы было разрешено срабатывание перехода 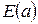 – функция, задающая выражения на дугах
– функция, задающая выражения на дугах 
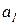 помечается двумя фишками типа
помечается двумя фишками типа 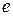 ;
;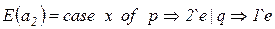
 помечается двумя фишками типа
помечается двумя фишками типа  и одной фишкой типа
и одной фишкой типа 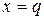 .
.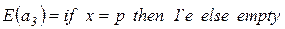
 помечается одной фишкой типа
помечается одной фишкой типа 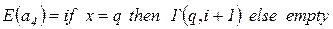
 помечается одной фишкой типа
помечается одной фишкой типа 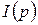 - функция инициализации сети CPN. Эта функция по аналогии с обыкновенными СП задает начальную маркировку (разметку) сети
- функция инициализации сети CPN. Эта функция по аналогии с обыкновенными СП задает начальную маркировку (разметку) сети 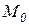 , т.е. для каждой позиции
, т.е. для каждой позиции 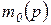 .
.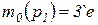 ;
;  ;
; 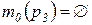 - начальные маркировки позиций;
- начальные маркировки позиций;  - начальная маркировка сети.
- начальная маркировка сети. . (3.8)
. (3.8)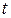 .
.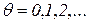 . Поэтому маркировку отдельных позиций
. Поэтому маркировку отдельных позиций 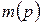 и сети в целом
и сети в целом 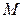 мы будем также привязывать ко времени и записывать соответственно в виде
мы будем также привязывать ко времени и записывать соответственно в виде 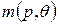 и
и  .
.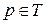 при осуществлении шага работы CPN рассчитывается по формуле:
при осуществлении шага работы CPN рассчитывается по формуле: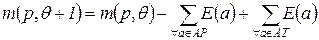 . (3.9)
. (3.9)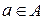 помечена отдельным выражением
помечена отдельным выражением 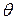 выполняются условия срабатывания нескольких переходов, то по аналогии с обыкновенными СП, в зависимости от задачи исследования CPN мы можем разрешить сработать всем переходам (при построении дерева возможных маркировок), либо дать такую возможность только одному из них на основе некоторых дополнительных условий (например, приоритетов).
выполняются условия срабатывания нескольких переходов, то по аналогии с обыкновенными СП, в зависимости от задачи исследования CPN мы можем разрешить сработать всем переходам (при построении дерева возможных маркировок), либо дать такую возможность только одному из них на основе некоторых дополнительных условий (например, приоритетов).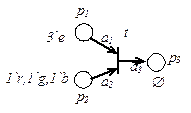
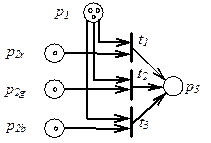
 ;
; 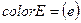 .
.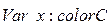 ;
; 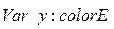 .
.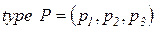 .
. .
.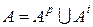 ,
,  ,
, 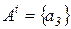 ,
, 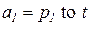 ,
, 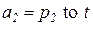 ,
, 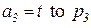
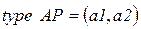 ;
; 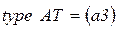 ;
;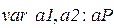 ;
; 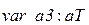 ;
;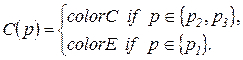
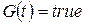 .
.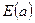 , задающая выражения на дугах:
, задающая выражения на дугах: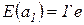 ;
;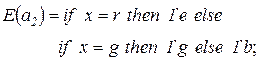
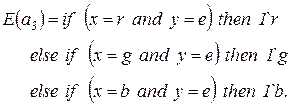
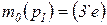 ;
; 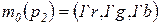 ;
; 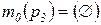 .
.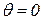

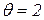
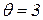

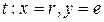

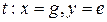
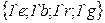
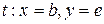
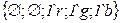
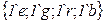
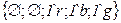
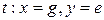

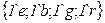
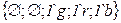
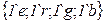
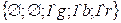
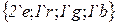


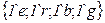
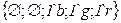
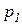 разрешен цвет
разрешен цвет 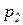 ,
, 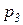 разрешены цвета
разрешены цвета 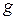 ,
, 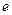 в позиции
в позиции 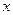 принимает поочередно (в произвольном порядке) значения
принимает поочередно (в произвольном порядке) значения 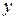 - значение
- значение 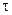 . Обычно это время считается дискретным, т.е. означает номер такта, выдаваемого тактовым генератором системы моделирования. Глобальное время
. Обычно это время считается дискретным, т.е. означает номер такта, выдаваемого тактовым генератором системы моделирования. Глобальное время  отличается от времени
отличается от времени 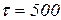 и далее готова для работы в сети, а запись @[500, 600] означает, что фишка может использоваться в диапазоне глобального времени
и далее готова для работы в сети, а запись @[500, 600] означает, что фишка может использоваться в диапазоне глобального времени 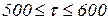 .
.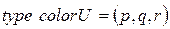 ;
; ;
; ;
;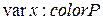 .
.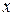 :
: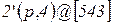 .
. , где
, где  - время задержки, задаваемое числом или функцией.
- время задержки, задаваемое числом или функцией.
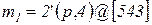 ,
, 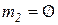 .
.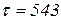 . Переход
. Переход 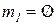 ,
,  .
. и
и 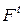 следует задавать множеством дуг
следует задавать множеством дуг 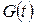 всегда истинна.
всегда истинна.


