
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели кратно-аддитивного типаСодержание книги
Поиск на нашем сайте
Способ логарифмирования Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае результат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечивается еще более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. Недостаток данного метода – ограничение сферы применения. Алгоритм расчета влияния факторов на величину результативного показателя для факторной модели вида
Стохастический анализ Стохастический анализ представляет собой методику исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при корреляционной связи изменение аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих данный показатель. Например, производительность труда при одном и том же уровне фондовооруженности может быть неодинаковой на разных предприятиях. Это зависит от оптимальности сочетания других факторов, воздействующих на этот показатель. Корреляционная (стохастическая) связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений. Отличают парную и множественную корреляцию. Парная корреляция – это связь между двумя показателями, один из которых является факторным, а второй – результативным. Множественная корреляция – возникает от взаимодействия нескольких факторов с результативным показателем. Необходимые условия применения корреляционного анализа: 1. Наличие большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов). 2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации. Применение корреляционного анализа позволяет решить следующие задачи: - определить изменение результативного показателя под воздействием одного или несколько факторов, т.е. определить насколько единиц изменяется величина результативного показателя при изменении факторного на единицу; - установить относительную степень зависимости результативного показателя от каждого фактора. Корреляционный анализ – метод установления связи и измерения ее тесноты между наблюдениями, которые можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону. Корреляционной связью называется такая статистическая связь, при которой различным значениям одной переменной соответствуют разные средние значения другой. Корреляционная связь может возникать несколькими путями. Важнейший из них – причинная зависимость вариации результативного признака от изменения факторного. Кроме того, такой вид связи может наблюдаться между двумя следствиями одной причины. Основной особенностью корреляционного анализа следует признать то, что он устанавливает лишь факт наличия связи и степень ее полноты, не вскрывая ее причин. В экономическом анализе теснота измеряется линейным коэффициентом корреляции. Коэффициент корреляции при прямолинейной форме связи между факторами х и у определяется следующим образом:
При измерении тесноты связи при криволинейной форме зависимости используется не линейный коэффициент корреляции, а корреляционной отношение, которое рассчитывается по формуле:
Данная формула является универсальной. Ее можно применять для исчисления коэффициента корреляции при любой форме зависимости. Однако для его нахождения требуется предварительное решение уравнения регрессии и расчет по нему теоретических (выравненных) значений результативного показателя для каждого наблюдения исследуемой выборки. Значения коэффициента корреляции изменяются в интервале [–1; +1]. Значение г = –1 свидетельствует о наличии жестко детерминированной обратно пропорциональной связи между факторами, г = +1 соответствует жестко детерминированной связи с прямо пропорциональной зависимостью факторов. Если линейной связи между факторами не наблюдается, то r = 0. Другие значения коэффициента корреляции свидетельствуют о наличии стохастической связи, причем, чем ближе /r/ к единице, тем связь теснее. При /r/ < 0,3 связь можно считать слабой; при 0,3 < /r/ < 0,7 – средней тесноты; при |г| > 0,7 – тесной. Если коэффициент корреляции возвести в квадрат, получим коэффициент детерминации. Он показывает насколько процентов результативный показатель зависит от факторного. Практическая реализация корреляционного анализа включает следующие этапы: - постановка задачи и выбор признаков; - сбор информации и ее первичная обработка (группировки, исключение, аномальных наблюдений, проверка нормальности одномерного распределения); - предварительная характеристика взаимосвязей (аналитические группировки, графики); - устранение мультиколлинеарности (взаимозависимости факторов) и уточнение набора показателей путем расчета парных коэффициентов корреляции; - исследование факторной зависимости и проверка ее значимости; - оценка результатов анализа и подготовка рекомендаций по их практическому использованию. Регрессионный анализ состоит из нескольких этапов. На первом этапе определяются факторы, которые оказывают воздействие на изучаемый показатель, и отбираются наиболее существенные для корреляционного анализа. Отбор факторов – очень важный момент в экономическом анализе: от того, насколько правильно он сделан, зависит точность выводов по итогам анализа. Не рекомендуется включать в корреляционную модель взаимосвязанные факторы. Если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа; нельзя включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер. Большую помощь при отборе факторов для корреляционной модели оказывают аналитические группировки, способ сравнения параллельных и динамических рядов, линейные графики. С их помощью можно определить наличие, направление и форму зависимости между изучаемыми показателями. Отбор факторов можно производить также в процессе решения задачи корреляционного анализа на основе оценки их значимости по критерию Стьюдента. На втором этапе собирается исходная информация по каждому факторному и результативному показателям. Она должна быть проверена на достоверность, на однородность и на соответствие закону нормального распределения. В первую очередь необходимо убедиться в достоверности информации, насколько она соответствует объективной действительности. Использование недостоверной, неточной информации приведет к неточным результатам анализа и к неправильным выводам. Одно из условий корреляционного анализа – однородность исследуемой информации относительно распределения ее около среднего уровня. Если в совокупности имеются группы объектов, которые значительно отличаются от среднего уровня, то это говорит о неоднородности исходной информации. Критерием однородности информации служат среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю. Среднеквадратическое отклонение показывает абсолютное отклонение индивидуальных значений от среднеарифметической. Оно определяется по формуле:
Коэффициент вариации показывает относительную меру отклонения отдельных значений от среднеарифметической. Для его расчета используется формула:
Чем больше коэффициент вариации, тем относительно больший разброс и меньшая выравненность изучаемых объектов. Изменчивость вариационного ряда принято считать незначительной, если вариация не превышает 10%, средней – если вариация составляет 10-12%, значительной - когда она больше 20%, но не превышает 33%. Если же вариация выше 33%, то это свидетельствует о неоднородности информации и о необходимости исключения нетипичных наблюдений, которые обычно бывают в первых и последних ранжированных рядах выборки. Следующее требование к исходной информации – подчинение ее закону нормального распределения. Для количественной оценки степени отклонения информации от нормального распределения служат отношение показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке. Показатель асимметрии (А) и его ошибка (me) рассчитываются по следующим формулам:
Показатель эксцесса (Е) и его ошибка (me) рассчитываются следующим образом:
В симметричном распределении А = 0. Отклонение от нуля указывает на наличие асимметрии в распределении данных около средней величины. Отрицательная асимметрия свидетельствует о том, что преобладают данные с большими значениями, а с меньшими значениями встречаются значительно реже. Положительная асимметрия показывает, что чаще встречаются данные с небольшими значениями. В нормальном распределении показатель эксцесса Е = 0. Если Е > 0, то данные густо сгруппированы около средней, образуя островершинность. Если Е < 0, то кривая распределения будет плосковершинной. Однако когда отношения A/me, E/me меньше 3, то асимметрия и эксцесс не имеют существенного значения, и исследуемая информация соответствует закону нормального распределения. Следовательно, ее можно использовать для корреляционного анализа. На третьем этапе изучается характер и моделируется связь между факторами и результативным показателями, т.е. подбирается и обосновывается математическое уравнение, которое наиболее точно отражает сущность исследуемой зависимости. Для его обоснования используются те же приемы, что и для установления наличия связи: аналитические группировки, линейные графики и др. На четвертом этапе производится расчет основных показателей связи корреляционного анализа: уравнение связи, коэффициенты корреляции, детерминации, эластичности и др. Пятый этап – статистическая оценка и практическое использование результатов корреляционного анализа. Для того чтобы убедиться в надежности показателей связи и правомерности их использования для практической цели, необходимо дать им статистическую оценку Для этого используются критерий Стьюдента (t), критерий Фишера (F-отношение), средняя ошибка аппроксимации (ε), коэффициенты множественной корреляции (R) и детерминации (D). Надежность коэффициентов корреляции, которая зависит от объема исследуемой выборки данных, проверяется по критерию Стьюдента:
Если расчетное значение t выше табличного, то можно сделать заключение о том, что величина коэффициента корреляции является значимой. Табличные значения t находят по таблице значений критериев Стьюдента. При этом учитываются количество степеней свободы (V= n - 1) и уровень доверительной вероятности (в экономических расчетах обычно 0,05 или 0,01). Надежность уравнения связи оценивается с помощью критерия Фишера, расчетная величина которого сравнивается с табличным значением. Если Fрасч > Fтабл, то гипотеза об отсутствии связи между исследуемыми показателями отвергается. Критерий Фишера рассчитывается следующим образом:
Yxi – индивидуальные значения результативного показателя, рассчитанные по уравнению;
Yi – фактическое индивидуальное значение результативного показателя; m – количество параметров в уравнении связи, учитывая свободный член уравнения; n – количество наблюдений.
Для оценки точности уравнения связи рассчитывается средняя ошибка аппроксимации. Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпирической), тем меньше ее величина, а это свидетельствует о правильности подбора формы уравнения связи. Средняя ошибка аппроксимации рассчитывается по формуле:
О полноте уравнения связи можно судить по коэффициентам множественной регрессии и детерминации. Если их значения близки к 1, значит в корреляционную модель удалось включить наиболее существенные факторы, на долю которых приходится основная вариация результативного показателя. Влияние каждого фактора на прирост (отклонение от плана) результативного показателя рассчитывается по формуле:
Коэффициенты регрессии в уравнении связи имеют разные единицы измерения, что делает их несопоставимыми, если возникает вопрос о сравнительной силе воздействия факторов на результативный показатель. Чтобы привести их в сопоставимый вид, все переменные уравнения регрессии выражают в долях среднеквадратического отклонения, т.е. рассчитывают стандартизированные коэффициенты регрессии или бетта-коэффициенты (β)
Бета-коэффициенты показывают, что если величина фактора увеличится на одно среднеквадратическое отклонение, то соответствующая зависимая переменная увеличится или уменьшится на долю своего среднеквадратического отклонения. Сопоставление бетта-коэффициентов позволяет сделать вывод о сравнительной степени воздействия каждого фактора на величину результативного показателя. Коэффициент эластичности рассчитывается по формуле:
Коэффициент эластичности показывает, на сколько процентов в среднем изменится функция с изменением аргумента на 1%. Перечисленное многообразие методов предоставляет аналитику широкие возможности в выборе инструментария исследования, как в экономическом анализе, так и в рамках финансового анализа. Выбор того или иного способа или приема из перечисленных определяется целью экономического (финансового) анализа, требованиями к степени детализации (глубины) анализа, к точности результатов (например, «разложение» результативного показателя по факторам), характером взаимосвязи между показателями, характером аналитических задач. Независимо от выбранных способов алгоритм решения практически любой аналитической задачи содержит приемы сравнения, группировки, балансовой увязки и графический, которые рассматриваются как способы обработки первичной, исходной информации.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.115.187 (0.008 с.) |










 .
. ;
;  ;
;
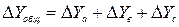 .
.
 где
где






 , где
, где - среднее значение результативного показателя, рассчитанного по уравнению;
- среднее значение результативного показателя, рассчитанного по уравнению;






