Простой категорический силлогизм

Силлогизм (от греч. sillogismos – подсчитывание, подытоживание, выведение следствия) – это другое название дедуктивного умозаключения. Существует несколько видов силлогизмов. Первый из них называется простым, или категорическим, потому что все суждения, входящие в него (две посылки и вывод), являются простыми, или категорическими. Это уже известные нам суждения видов А, I, Е, О.

Рассмотрим пример простого силлогизма.

Все цветы (М) – это растения (Р).

Все розы ( S) – это цветы (М).

Все розы ( S) – это растения (Р).

 

Обе посылки и вывод являются в данном силлогизме простыми суждениями (причем и посылки, и вывод – это суждения вида А (общеутвердительные)). Обратим внимание на вывод, представленный суждением: Все розы – это растения. В этом выводе субъектом выступает термин розы, а предикатом – термин растения. Субъект вывода присутствует во второй посылке силлогизма, а предикат вывода – в первой. Также в обеих посылках повторяется термин цветы, который, как нетрудно увидеть, является связующим: именно благодаря ему не связанные, разобщенные в посылках термины растения и розы возможно связать в выводе. Таким образом, структура силлогизма включает в себя две посылки и один вывод, которые состоят из трех (различным образом расположенных) терминов.

1. Субъект вывода располагается во второй посылке силлогизма и называется меньшим термином силлогизма (вторая посылка также называется меньшей).

2. Предикат вывода располагается в первой посылке силлогизма и называется большим термином силлогизма (первая посылка также называется большей). Предикат вывода, как правило, является по объему большим понятием, чем субъект вывода (в приведенном примере понятия розы и растения находятся в отношении родовидового подчинения), в силу чего предикат вывода назван большим термином, а субъект вывода – меньшим.

3. Термин, который повторяется в двух посылках и связывает субъект с предикатом (меньший и больший термины), называется средним термином силлогизма и обозначается латинской буквой М, потому что «средний» на латинском – это medium.

Три термина силлогизма могут быть расположены в нем по-разному. Взаимное расположение терминов друг относительно друга называется фигурой простого силлогизма. Таких фигур четыре, то есть все возможные варианты взаимного расположения терминов в силлогизме исчерпываются четырьмя комбинациями. Рассмотрим их.

Первая фигура силлогизма – это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. Например:

Все газы (М) – это химические элементы (Р).

Гелий ( S) – это газ (М).

Гелий ( S) – это химический элемент (Р).

 

Учитывая то, что в первой посылке средний термин связан с предикатом, во второй – субъект связан со средним термином, а в выводе субъект связан с предикатом, составим схему расположения и связи терминов в приведенном примере:

 

 

Прямые линии на схеме (за исключением той, которая отделяет посылки от вывода) показывают связь терминов в посылках и в выводе. Поскольку роль среднего термина заключается в том, чтобы связывать больший и меньший термины силлогизма, то на схеме средний термин в первой посылке соединяется линией со средним термином во второй посылке. Схема показывает, каким именно образом средний термин связывает между собой другие термины силлогизма в его первой фигуре. Кроме того, можно изобразить отношения между тремя терминами с помощью кругов Эйлера. В данном случае получится следующая схема:

 

 

Вторая фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином. Например:

 

Все рыбы (Р) дышат жабрами (М).

Все киты ( S) не дышат жабрами (М).

Все киты ( S) не рыбы (Р).

 

Схемы взаимного расположения терминов и отношений между ними во второй фигуре силлогизма выглядят так:

 

 

Третья фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Например:

Все тигры ( M) – это млекопитающие (Р).

Все тигры (М) – это хищники ( S).

Некоторые хищники ( S) – это млекопитающие (Р).

 

Схемы взаимного расположения терминов и отношений между ними в третьей фигуре силлогизма:

 

 

Четвертая фигура силлогизма – это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него. Например:

 

Все квадраты (Р) – это прямоугольники (М).

Все прямоугольники (М) – это не треугольники ( S).

Все треугольники ( S) – это не квадраты (Р).

 

Схемы взаимного расположения терминов и отношений между ними в четвертой фигуре силлогизма:

 

 

(Отметим, что отношения между терминами силлогизма во всех фигурах могут быть и другими.)

Любой простой силлогизм состоит из трех суждений (двух посылок и вывода). Каждое из них является простым и принадлежит к одному из четырех видов (А, I, E, О.) Набор простых суждений, входящих в силлогизм, называется модусом простого силлогизма.

Например, в силлогизме:

Все небесные тела движутся.

Все планеты – это небесные тела.

Все планеты движутся.

 

первая посылка является простым суждением вида А (общеутвердительным), вторая посылка – это тоже простое суждение вида А, и вывод в данном случае представляет собой простое суждение вида А. Поэтому рассмотренный силлогизм имеет модус ААА. Силлогизм:

Все журналы – это периодические издания.

Все книги не являются периодическими изданиями.

Все книги не являются журналами.

имеет модус АЕЕ. Силлогизм:

Все углероды – простые тела.

Все углероды электропроводны.

Некоторые электропроводники – простые тела.

 

имеет модус AAI. Всего модусов во всех четырех фигурах, то есть возможных комбинаций простых суждений в силлогизме, – 256. В каждой фигуре 64 модуса. Однако из всех этих 256 модусов только 19 дают достоверные выводы, остальные приводят к вероятностным выводам. Если принять во внимание, что одним из главных признаков дедукции (а значит, и силлогизма) является достоверность ее выводов, то становится понятным, почему эти 19 модусов называются правильными, а остальные – неправильными.

Наша задача – уметь определять фигуру и модус любого простого силлогизма. Например, требуется установить фигуру и модус силлогизма:

 

Все вещества состоят из атомов.

Все жидкости – это вещества.

Все жидкости состоят из атомов.

 

Прежде всего надо найти субъект и предикат вывода, то есть меньший и больший термины силлогизма. Далее следует установить местоположение меньшего термина во второй посылке и большего в первой. После этого можно определить средний термин и схематично изобразить расположение всех терминов в силлогизме:

Все вещества (М) состоят из атомов (Р).

Все жидкости ( S) – это вещества (М).

Все жидкости ( S) состоят из атомов (Р).

 

 

Как видим, рассматриваемый силлогизм построен по первой фигуре. Теперь надо найти его модус. Для этого следует выяснить, к какому виду простых суждений относятся первая посылка, вторая и вывод. В нашем примере обе посылки и вывод являются суждениями вида А (общеутвердительными), то есть модус данного силлогизма – ААА. Итак, предложенный силлогизм имеет первую фигуру и модус ААА.

Вывод простого силлогизма является истинным конечно же в том случае, когда истинны его посылки. Однако истинность посылок – это недостаточное условие истинности вывода. Вполне может быть так, что обе посылки в силлогизме истинны, а вывод его ложен. Например:

Все дети обладают мышлением.

Все взрослые – это не дети.

Все взрослые не обладают мышлением.

 

В этом силлогизме, построенном по первой фигуре и имеющем модус АЕЕ, и первая, и вторая посылки являются истинными суждениями, из которых вытекает ложный вывод. Почему так получается? Потому что при построении силлогизма следует обращать внимание не только на то, чтобы посылки были истинными, но и в не меньшей степени на то, чтобы были соблюдены определенные требования или правила его построения, которые мы рассмотрим в следующем параграфе.

 

Правила простого силлогизма

 

Как уже говорилось, для получения истинного вывода в простом силлогизме недостаточно одной только истинности его посылок. Надо также соблюдать определенные требования или правила его построения. Правила силлогизма делятся на общие и частные. Общие правила применимы ко всем простым силлогизмам, независимо от того, по какой фигуре они построены. Частные правила действуют только для каждой фигуры силлогизма и поэтому часто называются правилами фигур.

 

Общие правила силлогизма

 

1. В силлогизме должно быть только три термина. Обратимся к уже упоминавшемуся (см. Введение) примеру силлогизма, в котором данное правило нарушено:

Движение вечно.

Хождение в школу – это движение.

Хождение в школу вечно.

 

Обе посылки этого силлогизма являются истинными суждениями, однако из них вытекает ложный вывод, потому что нарушено рассматриваемое правило. Термин движение употребляется в двух посылках в двух разных смыслах (движение как всеобщее мировое изменение и движение как механическое перемещение тела из точки в точку), и получается, что терминов в силлогизме три {движение, хождение в школу, вечность), а смыслов (поскольку один из терминов употребляется в двух разных смыслах) четыре, то есть лишний смысл как бы подразумевает лишний термин. Иначе говоря, в приведенном примере силлогизма было не три, а четыре (по смыслу) термина. Ошибка, возникающая при нарушении вышеприведенного правила, называется учетверением терминов.

2. Средний термин должен быть распределен хотя бы в одной из посылок. Ораспределенности терминов в простых суждениях речь шла в предыдущей главе (см. § 2.3). Напомним, что проще всего устанавливать распределенность терминов в простых суждениях с помощью круговых схем: надо изобразить кругами Эйлера отношения между терминами суждения, при этом полный круг на схеме будет обозначать распределенный термин (+), а неполный – нераспределенный (–). Рассмотрим пример силлогизма:

Все кошки – это живые существа.

Сократ – это тоже живое существо.

Сократ – это кошка.

 

Из двух истинных посылок вытекает ложный вывод. Изобразим кругами Эйлера отношения между терминами в посылках силлогизма и установим распределенность этих терминов:

 

 

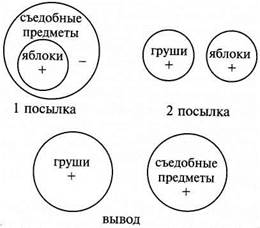
Как видим, средний термин (живые существа) в данном случае нераспределен ни в одной из посылок, а по правилу он должен быть распределен хотя бы в одной из посылок. Ошибка, возникающая при нарушении рассматриваемого правила, так и называется – нераспределенность среднего термина в каждой посылке.

3. Термин, который был нераспределен в посылке, не может быть распределен в выводе. Обратимся к следующему примеру:

Все яблоки съедобны.

Все груши – это не яблоки.

Все груши несъедобны.

 

Посылки силлогизма являются истинными суждениями, а вывод – ложным. Как и в предыдущем случае, изобразим кругами Эйлера отношения между терминами в посылках и в выводе силлогизма и установим распределенность этих терминов:

 

 

В данном случае предикат вывода, или больший термин силлогизма {съедобные предметы) в первой посылке является нераспределенным (–), а в выводе – распределенным (+), что запрещается рассматриваемым правилом. Ошибка, возникающая при его нарушении, называется расширением большего термина. (Вспомним, что термин распределен, когда речь идет обо всех предметах, входящих в него, и нераспределен, когда речь идет о части предметов, входящих в него, именно поэтому ошибка и называется расширением термина.)

4. В силлогизме не должно быть двух отрицательных посылок. Хотя бы одна из посылок силлогизма должна быть положительной (могут быть положительными и обе посылки). Если две посылки в силлогизме отрицательные, то вывод из них или вообще сделать нельзя, или же, если его сделать возможно, он будет ложным (или, по крайней мере, недостоверным, вероятностным). Например:

Снайперы не могут иметь плохое зрение.

Все мои друзья – не снайперы.

Все мои друзья имеют плохое зрение.

 

Обе посылки в силлогизме являются отрицательными суждениями, и, несмотря на их истинность, из них вытекает ложный вывод. Ошибка, которая возникает в данном случае, так и называется – две отрицательные посылки.

5. В силлогизме не должно быть двух частных посылок. Хотя бы одна из посылок должна быть общей (могут быть общими и обе посылки). Если две посылки в силлогизме представляют собой частные суждения, то вывод из них сделать невозможно. Например, из следующих посылок:

Некоторые школьники – это первоклассники.

Некоторые школьники – это десятиклассники.

?

 

никакой вывод не следует, потому что обе они являются частными. Ошибка, возникающая при нарушении данного правила, так и называется – две частные посылки.

6. Если одна из посылок отрицательная, то и вывод должен быть отрицательным. Например:

Ни один металл не является изолятором.

Медь – это металл.

Медь не является изолятором.

 

Как видим, из двух посылок данного силлогизма не может вытекать утвердительный вывод. Он может быть только отрицательным.

7. Если одна из посылок частная, то и вывод должен быть частным. Например:

Все углеводороды – это органические соединения.

Некоторые вещества – это углеводороды.

Некоторые вещества – это органические соединения.

 

В этом силлогизме из двух посылок не может следовать общий вывод. Он может быть только частным, так как вторая посылка является частной.

Таковы общие правила простого силлогизма. Теперь перечислим частные правила, или правила фигур силлогизма.

Для первой фигуры: большая посылка должна быть общей, меньшая – утвердительной.

Для второй фигуры: большая посылка должна быть общей, одна из посылок и вывод должны быть отрицательными.

Для третьей фигуры: меньшая посылка должна быть утвердительной, а вывод – частным.

Для четвертой фигуры: если большая посылка утвердительная, то меньшая посылка должна быть общей; если одна из посылок отрицательная, то большая должна быть общей.