Допущено Учебно-методическим объединением

Допущено Учебно-методическим объединением

по специальностям педагогического образования

в качестве учебного пособия для студентов высших учебных заведений,

обучающихся по педагогическим специальностям

(ГСЭ.Р.ОО – национально-региональный (вузовский) компонент)

Рекомендовано Учебно-методическим центром

«Профессиональный учебник» в качестве учебного пособия

для студентов вузов, обучающихся по педагогическим специальностям

 

УДК 16(075.8)

ББК 87.4я73

Г96

 

Рецензенты:

кафедра философии и религиоведения

Московского государственного университета культуры и искусств (МГУКИ)

(зав. кафедрой канд. истор. наук, проф. И.Н. Романов);

д-р филос. наук, проф. С.Н. Мареев

(гл. науч. сотр. Института профессионального послевузовского образования

Современной гуманитарной академии)

 

Главный редактор издательства

кандидат юридических наук,

доктор экономических наук Н.Д. Эриашвили

 

Гусев Д.А.

Г96 Логика: Учеб. пособие для вузов. – М.: ЮНИТИ-ДАНА, 2004. – 272 с. – (Серия «Высшее профессиональное образование: Педагогика»).

 

ISBN 5-238-00723-Х

 

Книга представляет собой стройное изложение основного содержания одной из научных дисциплин – логики, которая, появившись приблизительно 2,5 тысячи лет назад, до настоящего времени сохраняет свою актуальность.

Материал изложен просто, ясно и интересно; приводятся многочисленные примеры, показывающие практическую значимость логики для современного человека. Книгу завершает тест по всему курсу науки, состоящий из 100 заданий, и развернутый словарь логических терминов.

Для студентов высших учебных заведений, обучающихся по педагогическим специальностям.

ББК 87.4я73

 

ISBN 5-238-00723-Х © Д.А. Гусев, 2004

© ИЗДАТЕЛЬСТВО ЮНИТИ-ДАНА, 2004.

Воспроизведение всей книги или какой-либо

ее части любыми средствами или в какой-либо

форме, в том числе в Интернет-сети, запрещается

без письменного разрешения издательства

 

Глава 1. ПОНЯТИЕ

Неопределенные понятия в логике

 

Понятия бывают определенными и неопределенными.

Понятие является определенным тогда, когда оно имеет ясное содержание и резкий объем. Как мы уже знаем, содержание понятия – это наиболее важные признаки того объекта, который оно выражает, а объем – это количество охватываемых им объектов. Таким образом, понятие имеет ясное содержание в том случае, если можно точно указать набор существенных признаков выражаемого объекта, а также точно установить границу между теми объектами, которые данное понятие охватывает, и теми, которые не принадлежат к его объему. Например, понятие мастер спорта является определенным. Оно имеет ясное содержание, так как можно точно указать наиболее важный отличительный признак мастера спорта – официально обладать этим спортивным разрядом. Также понятие мастер спорта имеет резкий объем – относительно любого человека можно точно сказать, является он мастером спорта или нет, то есть попадает или не попадает в объем этого понятия; говоря иначе, возможно провести резкую границу между всеми мастерами спорта и всеми, кто ими не является, точно отделить одних от других.

Понятие является неопределенным тогда, когда оно имеет неясное содержание и нерезкий объем. Если понятие характеризуется неясным содержанием, то значит, что невозможно точно указать наиболее важные отличительные признаки того объекта, который оно выражает; а нерезкий объем понятия свидетельствует о невозможности провести точную границу между теми объектами, которые входят в объем этого понятия, и теми, которые не входят в него. Например, понятие хороший спортсмен является неопределенным. Оно имеет неясное содержание, так как невозможно с точностью указать существенные признаки хорошего спортсмена: нельзя однозначно ответить на вопрос – кто это такой, кого следует считать хорошим спортсменом? То ли это тот, кто имеет разряд не ниже мастера спорта, то ли тот, кто установил не менее одного мирового рекорда, то ли – многократный олимпийский чемпион, то ли хороший спортсмен – это тот, кто сам себя таковым считает... Понятно, что и мнения различных людей по поводу того, кого надо относить к хорошим спортсменам, будут значительно различаться: одни будут утверждать одно, другие – другое. Также понятие хороший спортсмен имеет нерезкий объем – относительно любого человека невозможно точно сказать, является он хорошим спортсменом или нет, то есть попадает или не попадает в объем этого понятия, говоря иначе, нельзя провести резкую границу между множеством хороших спортсменов и всеми, кто ими не является, точно отделить одних от других.

Объем и содержание понятия, как уже говорилось в предыдущем параграфе, тесно связаны друг с другом. Только если в количественном отношении связь между ними обратная (чем больше объем понятия, тем меньше его содержание, и наоборот), то в качественном отношении эта связь прямая: ясное содержание понятия обусловливает его резкий объем, а неясному содержанию обязательно соответствует нерезкий объем, и, разумеется, наоборот.

Конечно же, намного удобнее и проще обращаться с определенными понятиями, чем с неопределенными, однако последние занимают значительное место и играют важную роль в мышлении и языке.

 

Отношения между понятиями

 

Понятия бывают сравнимыми (например, Москва и столица России, писатель и россиянин, город и населенный пункт, лев и тигр, горячая вода и холодная вода, высокий человек и невысокий человек) и несравнимыми (например, пингвин и кирпич, треугольник и президент, учебное заведение и небесное тело, спортсмен и город, книга и небоскреб, растение и государство).

Сравнимые понятия бывают совместимыми и несовместимыми. Совместимыми называются понятия, объемы которых имеют общие элементы, каким-либо образом соприкасаются. Например, понятия спортсмен и американец совместимые, так как их объемы имеют общие элементы или объекты: есть такие спортсмены, которые являются американцами, и, наоборот, есть такие американцы, которые являются спортсменами. Несовместимыми называются понятия, объемы которых не имеют общих элементов, никаким образом не соприкасаются. Например, понятия треугольник и квадрат являются несовместимыми, потому что их объемы не имеют общих элементов: ни один треугольник не может быть квадратом и наоборот.

Совместимые понятия могут быть в отношениях равнозначности, пересечения и подчинения.

 

 

Понятия находятся в отношении равнозначности в том случае, если их объемы полностью совпадают. Например, равнозначными будут понятия квадрат и равносторонний прямоугольник, так как любой квадрат – это равносторонний прямоугольник, а любой равносторонний прямоугольник – это квадрат. В логике принято изображать отношения между понятиями с помощью круговых схем Эйлера (известный математик XVIII в.): одно понятие, а вернее, его объем, изображается одним кругом, а второе, то есть его объем, – другим. Взаимное расположение этих кругов на схеме (они могут полностью совпадать или пересекаться, или не соприкасаться, или один круг располагается внутри другого) и показывает то или иное отношение между понятиями. Так, отношение равнозначности между понятиями квадрат и равносторонний прямоугольник изображается схемой, на которой два круга, обозначающие два равных объема, полностью совпадают.

Понятия находятся в отношении пересечения тогда, когда их объемы совпадают только частично. Например, пересекающимися будут понятия школьник и спортсмен: есть такие школьники, которые являются спортсменами, и есть такие спортсмены, которые являются школьниками; но в то же время школьник может не быть спортсменом, так же как и спортсмен может не быть школьником. На схеме Эйлера отношение пересечения изображается двумя пересекающимися кругами (заштрихованная часть показывает частично совпадающие объемы двух понятий).

 

 

Понятия находятся в отношении подчинения в том случае, когда объем одного из них обязательно больше объема другого и полностью его в себя включает (один объем как бы подчиняется другому). Например, в отношении подчинения находятся понятия карась и рыба, так как все караси – это обязательно рыбы, но рыбами являются не только караси, есть и другие виды рыб. Таким образом, объем понятия карась является меньшим по отношению к объему понятия рыба и полностью в него включается (подчиняется ему). В отношении подчинения понятия с меньшим объемом называются видовыми, а с большим – родовыми. На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого.

 

 

Отношениями равнозначности, пересечения и подчинения исчерпываются все случаи совместимости между понятиями.

Несовместимые понятия могут быть в отношениях соподчинения, противоположности и противоречия.

 

 

Понятия находятся в отношении соподчинения тогда, когда их объемы не имеют общих элементов, но в то же время входят в объем какого-то третьего понятия, родового для них (совместно ему подчиняются). Например, понятия сосна и береза являются соподчиненными: ни одна сосна не может быть березой и наоборот, но и множество всех сосен, и множество всех берез включается в более широкий объем понятия дерево. На схеме Эйлера отношение соподчинения изображается двумя несоприкасающимися кругами.

Понятия находятся в отношении противоположности в том случае, если они обозначают какие-то взаимоисключающие признаки, крайние состояния чего-либо, между которыми, однако, всегда есть некий средний, переходный вариант. Например, противоположными являются понятия высокий человек и низкий человек (третьим или переходным вариантом между ними будет понятие человек среднего роста). На схеме Эйлера отношение противоположности изображается двумя несоприкасающимся кругами, которые находятся как бы на разных «полюсах».

 

 

Поскольку объемы противоположных понятий не соприкасаются, это отношение отчасти похоже на соподчинение. Однако понятия, находящиеся в отношении соподчинения, обозначают просто различные объекты разных видов и одного рода, но не противоположные друг другу. Не можем же мы утверждать, что сосна является противоположностью березы, а береза – противоположностью сосны: это просто разные деревья, и не более того. В то же время высокий человек представляет собой противоположность низкого человека, и наоборот. Так же противоположными будут понятия темная комната и светлая комната, горячая вода и холодная вода, белый лист и черный лист, глубокая речка и мелкая речка и т.п.

 

 

Понятия находятся в отношении противоречия, если одно из них представляет собой отрицание другого, причем в отличие от противоположных понятий между противоречащими понятиями никак не может быть третьего или среднего варианта. Например, в отношении противоречия находятся понятия высокий человек и невысокий человек. В том случае, когда одно понятие является отрицанием другого, третий вариант автоматически исключается: и низкий человек, и человек среднего роста – это невысокий человек. На схеме Эйлера отношение противоречия изображается одним кругом, поделенным на две части, которые обозначают противоречащие понятия.

Отношениями соподчинения, противоположности и противоречия исчерпываются все случаи несовместимости между понятиями.

Итак, в логике выделяется шесть вариантов отношений между понятиями. Для удобства их запоминания они представлены в следующей таблице.

Любые два сравнимых понятия обязательно находятся в одном из шести указанных случаев отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек – подчинения, Москва и столица России – равнозначности, Москва и Петербург – соподчинения, мокрая дорога и сухая дорога – противоположности, Антарктида и материк – подчинения, Антарктида и Африка – соподчинения и т.д. и т.п.

 

 

Надо обратить внимание на то, что если два понятия обозначают часть и целое, например месяц и год, то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако если бы понятия месяц и год были подчиненными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий карась и рыба: карась – это обязательно рыба, но рыба – это не обязательно карась). Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия месяц и год, так же как и понятия книга и страница книги, автомобиль и колесо автомобиля, молекула и атом и т.п., находятся в отношении соподчинения, так как часть и целое – не то же самое, что вид и род.

 

 

В начале данного параграфа говорилось о том, что понятия бывают сравнимыми и несравнимыми. Считается, что рассмотренные шесть вариантов отношений применимы только к сравнимым понятиям. Однако возможно утверждать, что все несравнимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин и небесное тело возможно рассматривать как соподчиненные, ведь пингвин – это не небесное тело, и наоборот, но в то же время объемы понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающего мира или нечто существующее, или философское понятие форма материи (ведь и пингвин и небесное тело – это различные объекты окружающего мира или различные формы материи).

Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причем до сих пор мы изображали схематично отношения между двумя понятиями, а это можно сделать и с большим количеством понятий. Например, отношения между понятиями боксер, негр и человек изображаются следующей схемой.

Взаимное расположение кругов показывает, что понятия боксер и негр находятся в отношении пересечения (боксер может быть негром и может им не быть, а также негр может быть боксером и может им не быть), а понятия боксер и человек, так же как и понятия негр и человек, находятся в отношении подчинения (любой боксер, и любой негр – это обязательно человек, но человек может не быть ни боксером, ни негром).

Рассмотрим отношения между понятиями дедушка, отец, мужчина, человек с помощью круговой схемы.

 

 

Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина.

Отношения между понятиями хищник, рыба, акула, пиранья, щука изображаются следующей схемой:

 

 

Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.

Подытоживая все сказанное, отметим, что отношения между понятиями – это отношения между их объемами. Значит, для того чтобы было возможно установить отношения между понятиями, их объем должен быть резким, а содержание, соответственно, ясным, то есть эти понятия должны быть определенными. Что касается неопределенных понятий, о которых шла речь в предыдущем параграфе, то установить точные отношения между ними достаточно сложно, фактически невозможно, ведь из-за неясности их содержания и нерезкости объема два каких-нибудь неопределенных понятия можно будет характеризовать как равнозначные или как пересекающиеся, или как подчиняющиеся и т.д. Например, возможно ли установить отношение между неопределенными понятиями неаккуратность и небрежность"? То ли это будет равнозначность, то ли подчинение – точно сказать невозможно. Таким образом, отношения между неопределенными понятиями являются также неопределенными.

 

Определение понятия

 

Мы часто сталкиваемся с такими выражениями, как «начнем с определения...», «дайте определение...», «запомните определение...», «это неверное определение...» и т.п. Что же такое определение? Давайте дадим определение определению.

В обыденном смысле определение – это ответ на вопрос, что собой представляет какой-то объект, свойство, явление. Если говорить более точно и научно, то определение понятия – это логическая операция, которая раскрывает его содержание.

Определения бывают явными и неявными. Явное определение ставит своей целью непосредственное раскрытие содержания некого понятия, прямой ответ на вопрос, чем является объект, который оно обозначает. Например, определение: Термометр – это физический прибор, предназначенный для измерения температуры – явное. Неявное определение раскрывает содержание понятия не прямо, а косвенно, с помощью того контекста, в котором это понятие употребляется. Например, из следующей фразы: Во время этого грандиозного эксперимента сверхточные термометры зафиксировали температуру в 1000°С косвенно следует ответ на вопрос, что такое термометр, вытекает неявное определение этого понятия. Неявные определения называются также контекстуальными. Понятно, что определениями в полном смысле этого слова надо считать явные определения. В дальнейшем речь пойдет именно о них.

Определения также бывают реальными и номинальными. Реальное определение раскрывает содержание понятия, обозначающего какой-то объект, а номинальное (от лат. nomen – имя) раскрывает значение термина, в котором выражено какое-либо понятие. Говоря проще, реальные определения посвящены объектам, а номинальные – терминам (словам). Например, определение: Термометр – это физический прибор, предназначенный для измерения температуры, – реальное, а определение: Слово «термометр» обозначает физический прибор, предназначенный для измерения температуры, – номинальное. Как видим, принципиальной разницы между реальными и номинальными определениями не существует. Они различаются, как правило, по форме, но не по сути.

Существует несколько способов определения понятия, но среди них выделяется классический способ, который заключается в том, что определяемое понятие подводится под ближайшее к нему родовое понятие, после чего следует указание на его видовое отличие. Например, определение: Астрономия – это наука о небесных телах построено по классическому способу. В нем определяемое понятие астрономия сначала подводится под ближайшее к нему родовое понятие наука (астрономия – это обязательно наука, но наука – это не обязательно астрономия), а потом указывается на видовое отличие астрономии от других наук (...о небесных телах).

Пользуясь классическим способом, вы сможете дать точное и правильное определение любому понятию (если, конечно же, определяемый объект или термин вам хорошо знаком, и вы знаете, что он собой представляет или что означает соответственно). Например, нам требуется дать определение понятию квадрат. Следуя классическому способу, сначала подведем его под родовое понятие: квадрат – это геометрическая фигура..., а затем укажем на его видовое отличие от других геометрических фигур, которое заключается в наличии равных сторон и прямых углов. Итак, квадрат – это геометрическая фигура, у которой все стороны равны и углы прямые. (Давая определение понятию квадрат, мы могли бы подвести его под более близкое родовое понятие прямоугольник, и тогда определение получилось быследующим: Квадрат – это прямоугольник, у которого все стороны равны, однако и приведенное выше определение квадрата раскрывает содержание соответствующего понятия и является верным.) Обратите внимание на то, что фактически все определения, встречающиеся в научной, учебной и справочной литературе (в толковых словарях, например) построены по классическому способу.

 

Логические правила определения

 

Существует несколько логических правил определения. Нарушение хотя бы одного из них приводит к тому, что содержание понятия не раскрывается и определение не достигает своей цели, являясь неверным. Рассмотрим эти правила и ошибки, возникающие при их нарушении.

1.Определение не должно быть широким, то есть определение не должно превышать своим объемом определяемое понятие. Например, определение: Солнце – это небесное тело является широким: определение – небесное тело – по объему намного больше определяемого понятия – Солнце. Из приведенного в качестве примера определения далеко не вполне понятно, что такое Солнце, ведь небесное тело – это и любая планета, и любая галактика и т.д. и т.п. В данном случае можно также сказать, что пользуясь классическим способом определения, мы подвели определяемое понятие Солнце под родовое понятие небесное тело, но не сделали второй шаг – не указали на его видовое отличие.

2. Определение не должно быть узким, то есть определение не должно быть по своему объему меньше определяемого понятия. Например, определение: Геометрия – это наука о треугольниках является узким. Геометрия действительно наука о треугольниках, но не только о них, а в нашем примере она сведена только к треугольникам, то есть определение получилось по объему меньше определяемого понятия, в результате чего из приведенного определения не совсем понятно, что такое геометрия, содержание понятия в данном случае не раскрывается.

Как видим, ошибка узкого определения противоположна ошибке широкого определения. Если определение не должно быть широким и не должно быть узким, то каким же тогда оно должно быть? Оно должно быть соразмерным, то есть определяемое понятие и определение должны быть равны друг другу. Вернемся к определению: Астрономия – это наука о небесных телах, которое является соразмерным. В этом примере определяемое понятие астрономия и определение наука о небесных телах находятся в отношении равнозначности (астрономия – это именно наука о небесных телах, а наука о небесных телах – это только астрономия). Определение является соразмерным тогда, когда между его первой частью (определяемым понятием) и второй (определением) можно поставить знак равенства или тождества. Если же вместо этого между первой и второй частью определения ставится знак «больше» или «меньше», то оно является ошибочным – широким или узким соответственно. В данном случае мы видим проявление одного из основных законов логики – закона тождества, который упоминался во введении к этой книге.

3. В определении не должно быть круга, то есть в определении нельзя употреблять понятия, которые являются определяемыми. Например, в определении: Клеветник – это человек, который занимается клеветой присутствует круг, поскольку понятие клеветник определяется через понятие клевета, то есть фактически – через самое себя. (Если бы, выслушав приведенное только что определение, мы спросили бы, что такое клевета, нам вполне могли бы ответить, что клевета – это то, чем занимается клеветник.) Присутствующий в определении круг (или, по-гречески, тавтолоηгия – повтор) приводит к тому, что содержание понятия не раскрывается и определение является ошибочным. Только на первый взгляд круг в определении может не показаться ошибкой. Наверняка найдутся люди, которые скажут, что из определения: Клеветник – это человек, который занимается клеветой вполне понятно и кто такой клеветник, и что такое клевета. Однако они могут так утверждать только потому, что им ранее было известно значение терминов клеветник и клевета. Станет ли понятно, что такое экзистенциализм из следующего кругового определения: Экзистенциализм – это философское направление XX в., в котором ставятся и всесторонне рассматриваются различные экзистенциальные вопросы и проблемы! Узнаем ли мы, что такое синергетика, благодаря такому круговому определению: Синергетика – это раздел современного естествознания, который изучает разнообразные синергетические явления и процессы?

4. Определение не должно быть двусмысленным, то есть в нем нельзя употреблять термины в переносном значении. Вспомним всем хорошо знакомое с детства определение: Лев – это царь зверей. В данном определении термин царь используется в переносном смысле, но, кроме этого, у него есть еще и прямой смысл. Получается, что в определении употребляется один термин, а возможных смыслов у него два, то есть определение является двусмысленным (вновь нарушается логический закон тождества: одно слово, два смысла – 1 ¹2). Двусмысленность вполне уместна в качестве художественного приема, но в определении она недопустима, поскольку содержание понятия в данном случае не раскрывается.

5. Определение не должно быть сложным и непонятным. Рассмотрим следующее определение: Энтропия – это термодинамическая функция, характеризующая часть внутренней энергии замкнутой системы, которая не может быть преобразована в механическую работу. Это определение взято не из научного доклада и не из докторской диссертации, а из учебника для студентов гуманитарных специальностей «Концепции современного естествознания». Данное определение не широкое и не узкое, в нем нет круга и двусмысленности, оно верно и с научной точки зрения. Это определение кажется безупречным за тем только исключением, что оно является сложным и непонятным для людей, которые не занимаются специально естественными науками, то есть для большинства людей. Определение должно быть понятным для того, кому оно адресовано, иначе при всей своей формальной правильности оно не будет раскрывать содержания понятия для своего адресата. Непонятные определения также называют некоммуникабельными, то есть создающими преграды для общения между людьми.

6. Определение не должно быть только отрицательным. Например, определение: Квадрат – это не треугольник является только отрицательным. Квадрат – это действительно не треугольник, но данное определение не раскрывает содержание понятия квадрат, ведь, указав на то, чем не является объект, обозначенный определяемым понятием, мы не указали на то, чем он является (окружность, трапеция, пятиугольник и т.п. – это тоже не квадрат). Определение может быть отрицательным в том случае, когда оно дополнено положительной частью. Например, определение: Квадрат – это не треугольник, а прямоугольник, у которого все стороны равны – правильное. Важно, чтобы определение не было только отрицательным.

Итак, основные ошибки, возникающие при нарушении правил определения понятия – это широкое определение, узкое определение, круг в определении, двусмысленное определение, сложное и непонятное определение, только отрицательное определение. Наша задача – не допускать этих ошибок и уметь находить их в различных встречающихся нам определениях.

 

Деление понятия

 

Если определение понятия раскрывает его содержание, то деление понятия – это логическая операция, которая раскрывает его объем.

Деление понятия состоит из трех частей: 1) делимое понятие; 2) результаты деления; 3) основание деления (признак, по которому производится деление). Например, в следующем делении: Люди бывают мужчинами и женщинами (или, что то же самое: Люди делятся на мужчин и женщин) делимым является понятие люди, результаты деления – это понятия мужчины и женщины, а основание данного деления – пол, так как люди в нем разделены по половому признаку.

В зависимости от основания деление может быть различным. Например: Люди бывают высокими, низкими и среднего роста (основание деления – рост); Люди бывают монголоидами, европеоидами и негроидами (основание деления – раса); Люди бывают учителями, врачами, инженерами и т.д. (основание деления – профессия). Иногда понятие делится дихотомически, то есть, в переводе с греческого – пополам, по типу А и не-А, например: Люди бывают спортсменами и не спортсменами. Дихотомическое деление всегда правильное, то есть в нем автоматически исключаются все возможные в делении ошибки, о которых речь пойдет далее.

Мы хорошо знаем, зачем нам нужна операция определения понятия: любое знакомство с каким-либо новым предметом начинается с определения. Теперь ответим на вопрос, какую роль в мышлении и языке выполняет операция деления понятия. Изучая разные науки, вы заметили, что ни одна из них не обходится без различных классификаций, то есть разделений каких-то областей действительности на группы, части, виды и т.п. (классификация растений в ботанике, животных – в зоологии, химических элементов – в химии и т.д.). Однако любая классификация – это не что иное, как логическая операция деления понятия. Только классификации могут быть обширными, подробными, научными, но также могут быть простыми, обыденными, повседневными. Когда мы говорим: Люди делятся на мужчин и женщин или Учебные заведения бывают начальными, средними и высшими, то в этом случае уже создаем пусть маленькую и простую, но классификацию. Итак, логическая операция деления понятия лежит в основе любой классификации, без которой не обходится ни научное, ни повседневное мышление.

 

Логические правила деления

 

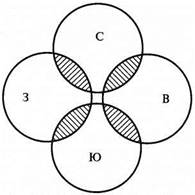
Существует несколько логических правил деления. Нарушение хотя бы одного из них приводит к тому, что объем понятия не раскрывается и деление не достигает своей цели, являясь неверным. Рассмотрим эти правила и ошибки, возникающие при их нарушении.

1.Деление должно проводиться по одному основанию, то есть при делении понятия следует придерживаться только одного выбранного признака. Например, в делении: Люди бывают мужчинами, женщинами и учителями используются два разных основания – пол и профессия, что недопустимо. Ошибка, возникающая при нарушении этого правила, называется подменой основания. В делении с подменой основания может использоваться не только два разных основания, как в приведенном выше примере, но и больше. Например, в делении: Люди бывают мужчинами, женщинами, китайцами и блондинами, как видим, используются три различных основания – пол, национальность и цвет волос, что конечно же тоже является ошибкой.

2. Деление должно быть полным, то есть надо перечислить все возможные результаты деления (суммарный объем всех результатов деления должен быть равен объему исходного делимого понятия). Например, деление: Учебные заведения бывают начальными и средними является неполным, так как не указан еще один результат деления – высшие учебные заведения. Но как быть, если надо перечислять не два или три, а десятки или сотни результатов деления. В этом случае можно употреблять понятия: и другие, и прочие, и так далее, и тому подобное, которые будут включать в себя неперечисленные результаты деления. Например: Люди бывают русскими, немцами, китайцами, японцами и представителями других национальностей.

3. Результаты деления не должны пересекаться, то есть понятиям, представляющим собой результаты деления, следует быть несовместимыми, их объемы не должны иметь общих элементов (на схеме Эйлера круги, обозначающие результаты деления, не должны соприкасаться, располагаясь отдельно друг от друга). Например, в делении: Страны мира делятся на северные, южные, восточные и западные допущена ошибка – пересечение результатов деления. Напервый взгляд приведенное в качестве примера деление кажется безошибочным: оно проведено по одному основанию (сторона света) и является полным (все стороны света перечислены). Чтобы увидеть ошибку в данном делении, надо рассуждать так. Возьмем какую-нибудь страну, например Канаду, и ответим на вопрос – является ли она северной? Конечно, является, так как расположена в Северном полушарии Земли. Теперь ответим на вопрос, является ли Канада западной страной? Да, потому что она расположена в Западном полушарии Земли. Таким образом, получается, что Канада – одновременно и северная, и западная страна, то есть она является общим элементом объемов понятий северные страны и западные страны, а значит, эти понятия пересекаются. То же самое можно сказать и относительно понятий южные страны и восточные страны. На схеме Эйлера результаты деления из нашего примера будут располагаться так:

 

 

Вспомним, каждая классификация построена таким образом, что любой элемент, попадающий в одну ее группу (часть, вид), ни в коем случае не попадает в другие. Это и есть следствие непересечения результатов деления или их взаимоисключения при составлении какой угодно классификации.

4. Деление должно быть последовательным, то есть не допускающим пропусков и скачков. Рассмотрим следующее деление: Леса бывают хвойными, лиственными, смешанными и сосновыми. Явно лишним здесь выглядит понятие сосновые леса, в силу чего допущенная в делении ошибка напоминает подмену основания (см. первое правило). Однако основание в данном случае не менялось: деление было проведено по одному и тому же основанию – тип древесных листьев. Подмена основания присутствует в таком, например, делении: Леса бывают хвойными, лиственными, смешанными, подмосковными и таежными. (Деление проведено по двум разным основаниям – тип древесных листьев и географическое местонахождение леса.) Вернемся к нашему первому примеру. Правильно было бы разделить леса на хвойные, лиственные и смешанные, а потом произвести второе деление – разделить хвойные леса на сосновые и еловые. Таким образом, надо было совершить два последовательных деления, а в приведенном примере второе деление пропущено, через него как бы перескочили, в результате чего два деления смешались в одно. Такая ошибка называется скачком в делении. Еще раз отметим, что скачок в делении не следует путать с подменой основания. Например, в делении: Учебные заведения бывают начальными, средними, высшими и университетами присутствует скачок, а в делении: Учебные заведения бывают начальными, средними, высшими и коммерческими допущена подмена основания.

Итак, основные ошибки, возникающие при нарушении правил деления понятия – это подмена основания, неполное деление, пересечение результатов деления и скачок в делении. Наша задача – правильно производить деление поняти