Краткий словарь логических терминов

Аналогия (или умозаключение по аналогии) – вид опосредованного умозаключения, в котором на основе сходства предметов в одних признаках делается вывод об их сходстве и в других признаках. Например:

Планета Земля расположена в Солнечной системе, на ней есть атмосфера, вода и жизнь.

Планета Марс расположена в Солнечной системе, на ней есть атмосфера и вода.

Вероятно, на Марсе есть жизнь.

Верификации принцип – один из критериев науки, наряду с принципом фальсификации, позволяющий отличить научное знание от псевдонаучного или ненаучного. В силу принципа верификации только то Знание является научным, которое можно в той или иной форме подтвердить.

Вопрос – логическая форма, которая направлена на получение ответа в виде некоторого суждения. Структура вопроса включает в себя две части. 1. Предпосылка (основная, или базисная, часть) вопроса – информация, выраженная каким-либо суждением. 2. Искомая часть вопроса – указание на недостаточность этой информации и необходимость ее дополнения каким-то ответом. Например, в вопросе: Когда была создана теория относительности? предпосылкой является суждение: Была создана теория относительности; а искомая часть выражена вопросительным словом когда. В логически корректном вопросе искомая часть является истинным суждением, например: С какой скоростью Земля вращается вокруг Солнца? В логически некорректном вопросе искомая часть – ложное суждение, например: Когда был создан первый автомобиль, способный передвигаться со скоростью света?

Гипотеза – предположение, как правило, научного характера, выдвигаемое с целью объяснения чего-либо (объектов, явлений, событий), которое впоследствии подтверждается или опровергается.

Гипотетико-дедуктивный метод – метод научного познания, по которому для объяснения каких-либо фактов выдвигается гипотеза, которая не только согласует между собой все эти факты и связывает их в единую картину, но и позволяет предсказать обнаружение новых фактов или, говоря иначе, из которой можно вывести (дедуцировать) все известные в какой-либо области действительности факты, а также получить указание на неизвестные (то есть пока не открытые) факты; впоследствии такая гипотеза превращается в научную теорию.

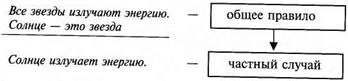
Дедукция (или дедуктивное умозаключение) – вид опосредованного умозаключения, в котором из общего правила выводится частный случай; в дедукции рассуждение идет от большего к меньшему, знание сужается, и поэтому ее выводы достоверны. Например:

 

Демонстрация – часть в структуре доказательства, наряду с тезисом и аргументами (основаниями), которая показывает, что тезис не просто связан с аргументами каким-либо образом, но и вытекает из них с достоверностью. Обычно демонстрация выражается в форме какого-либо умозаключения (как правило – дедуктивного).

Деление понятия – логическая операция, которая раскрывает объем понятия на основе какого-либо признака (основание деления). Например: Учебные заведения бывают начальными, средними и высшими; Учебные заведения бывают отечественными и зарубежными; Учебные заведения бывают престижными и не престижными и т.п.

Деление понятия дихотомическое – деление понятия строго на два объема, пополам, по типу А и не-А. Например: Люди бывают спортсменами и не спортсменами.

Дизъюнкция (или дизъюнктивное суждение) – вид сложного суждения, образованного из простых суждений при помощи союза «или»; дизъюнкция бывает нестрогой, когда ее элементы (входящие в нее простые суждения) друг друга не исключают (например: Петров изучает английский, или он изучает немецкий) и строгой, когда ее элементы друг друга исключают (например: Петров родился в 1969 году, или он родился в 1971 году).

Дилемма – разновидность условно-разделительного силлогизма, в первой посылке которого из одного или двух оснований вытекает два или одно следствие, вторая посылка является дизъюнкцией оснований или следствий, а вывод представляет собой утверждение следствия или дизъюнкции следствий (конструктивная дилемма простая и сложная соответственно) или же отрицание основания или дизъюнкции оснований (деструктивная дилемма простая и сложная соответственно). Например:

Если государь разумен, то общество процветает, а если он тиран, то общество бедствует.

Государь может быть разумным или тираном.

Общество может процветать или бедствовать.

(Сложная конструктивная дилемма.)

Доказательство – совокупность приемов подтверждения или опровержения чего-либо; оно состоит из трех частей:

а) тезис – что доказывается;

б) аргументы или основания – чем доказывается;

в) демонстрация – как доказывается или способ связи аргументов с тезисом.

По цели доказательства делятся на подтверждение и опровержение, а по способу демонстрации – на прямые и косвенные.

Доказательство косвенное – доказательство, в котором истинность или ложность тезиса устанавливается с помощью выяснения, соответственно, ложности или истинности антитезиса – высказывания, противоречащего тезису. Если невозможно напрямую подтвердить или опровергнуть тезис, тогда выдвигается антитезис и определяется его истинностное значение: если он истинен, то тезис (по закону исключенного третьего) ложен; если антитезис ложен, то тезис истинен.

Доказательство непосредственное – доказательство, в котором тезис подтверждается или опровергается путем его соотнесения с действительностью. Например, для того чтобы установить истинность или ложность тезиса: Сейчас на улице идет дождь, достаточно выглянуть в окно. Непосредственные доказательства также называются эмпирическими.

Доказательство опосредованное – доказательство, в котором тезис подтверждается или опровергается с помощью других тезисов (положений, утверждений, высказываний), истинность которых установлена ранее. Такое доказательство используется в тех случаях, когда подтвердить или опровергнуть тезис непосредственно, или эмпирически, невозможно. Предметом логического анализа являются опосредованные доказательства (в отличие от непосредственных).

Доказательство прямое – доказательство, в котором истинность или ложность тезиса устанавливается без выдвижения антитезиса и выяснения его истинностного значения.

Закон достаточного основания – один из основных законов логики, по которому любая мысль или тезис, для того чтобы иметь силу, должна быть доказана или обоснована какими-либо аргументами или основаниями; причем эти основания должны быть достаточными для доказательства исходной мысли или тезиса, то есть тезис должен вытекать из оснований с достоверностью.

Закон исключенного третьего – один из основных законов логики, по которому два противоречащих суждения об одном и том же предмете, в одно и то же время и в одном и том же отношении не могут быть одновременно истинными и не могут быть одновременно ложными.

Законы мышления (или законы логики) – объективные принципы или правила мышления, соблюдение которых всегда приводит рассуждение (независимо от его содержания) к истинным выводам при условии истинности исходных суждений.

Закон противоречия – один из основных законов логики, по которому два противоположных суждения об одном и том же предмете, в одно и то же время и в одном и том же отношении не могут быть одновременно истинными, но могут быть одновременно ложными.

Закон тождества – один из основных законов логики, по которому любая мысль должна быть равна' самой себе, то есть должна быть ясной, точной и определенной (нельзя подменять и путать понятия, создавать двусмысленность, уклоняться от темы, употреблять одни и те же слова в разных значениях или вкладывать одни и те же значения в разные слова и т.п.).

Импликация (или импликативное суждение) – вид сложного суждения, образованного из простых суждений при помощи условного союза «если... то», например: Если вещество является металлом, то оно электропроводно. Первая часть импликации – это основание, а вторая часть – следствие; из основания обязательно вытекает следствие, но из следствия не вытекает основание (например, из того, что вещество – металл, обязательно вытекает его электропроводность, но из того, что вещество электропроводно, не вытекает, что оно является металлом).

Индукция (или индуктивное умозаключение) – вид опосредованного умозаключения, в котором из нескольких частных случаев выводится общее правило; в индукции рассуждение идет от меньшего к большему, знание расширяется, и поэтому ее выводы чаще всего вероятностны. Например:

 

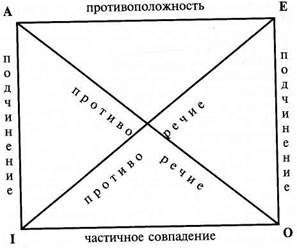
Квадрат логический – схематичное изображение отношений между простыми сравнимыми суждениями (А, I, E, О); вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними.

 

Квантор – указатель на объем субъекта простого суждения (в роли квантора могут быть слова все, некоторые, ни один и т.п.,).

Контрадикторность (или противоречие) – 1. Логическое отношение между понятиями, одно из которых является отрицанием другого, и между которыми не может быть третьего, среднего варианта, например высокий человек и невысокий человек, правда и неправда и т.п. 2. Логическое отношение между двумя простыми сравнимыми суждениями, которые не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них с необходимостью означает ложность другого, и наоборот, например: Все люди изучали логику и Некоторые люди не изучали логику. Это отношение между простыми суждениями видов А и О, Е и I.

Контрарность (или противоположность) – 1. Логическое отношение между понятиями, одно из которых исключает или отрицает другое, но между которыми всегда есть третий, средний вариант, например высокий человек и низкий человек (третий вариант – человек среднего роста), горячая вода и холодная вода (третий вариант – теплая вода) и т.п. 2. Логическое отношение между двумя простыми сравнимыми суждениями, которые не могут быть одновременно истинными, но могут быть одновременно ложными, потому что между ними всегда есть третий, промежуточный вариант, например: Все люди изучали логику и Все люди не изучали логику (третий вариант – Некоторые люди изучали логику, а некоторые не изучали). Это отношение между простыми суждениями видов А и Е.

Конъюнкция (или конъюнктивное суждение) – вид сложного суждения, образованного из простых суждений при помощи соединительного союза «и», например: Сверкнула молния, и загремел гром.

Круг в определении (или тавтология) – вид ошибки в определении понятия, которая заключается в том, что определение в той или иной степени повторяет определяемое понятие, в силу чего содержание последнего не раскрывается, например: Фильтрование – это процесс разделения какого-либо вещества с помощью специального приспособления – фильтра; Революция – это крупное историческое событие, которое приводит к революционным преобразованиям в обществе.

Логика (или формальная логика) – наука о формах и законах правильного мышления, которая появилась приблизительно в V в. до н.э. в Древней Греции и до сих пор сохраняет свое практическое значение.

Логика интуитивная – неявное знание и неосознанное (чаше всего) практическое использование основных принципов правильного мышления, которое формируется стихийно в процессе жизненного опыта приблизительно к шести-семи годам жизни человека.

Логика символическая (или математическая, или современная логика) – разновидность формальной логики, появившаяся в XIX в. и ставящая своей целью полную формализацию или математизацию содержательных рассуждений; попытка представить последние целиком в виде математических исчислений.

Логика традиционная – то же, что и аристотелевская логика, появившаяся приблизительно в V в. до н.э. в Древней Греции, дошедшая с незначительными изменениями до современной эпохи и поныне сохраняющая практическое значение.

Модус простого силлогизма – совокупность простых суждений (А, I, Е, О) – посылок и вывода силлогизма. Например, силлогизм:

Все живые организмы питаются влагой.

Все растения – это живые организмы.

Все растения питаются влагой.

 

имеет модус ААА, так как все его суждения (посылки и вывод) являются простыми суждениями вида А.

Обобщение понятия – логическая операция перехода от видового понятия к родовому с помощью исключения из его содержания каких-либо признаков. Например, если из содержания понятия квадрат исключить признак «иметь прямые углы и равные стороны», то это понятие превратится в более широкое по объему понятие – геометрическая фигура, которое будет родовым по отношению к видовому понятию квадрат.

 

Обращение (или конверсия) – способ преобразования простого суждения, который заключается в том, что его субъект и предикат меняются местами. Например, суждение Все караси ( S) являются рыбами (Р), преобразуется путем обращения так: Некоторые рыбы ( S) являются карасями (Р). Обращение также считается одним из видов непосредственных умозаключений.

Объем понятия – количество объектов, охватываемых этим понятием. Например, понятие человек охватывает собой огромное количество объектов (то есть всех людей), в объем же понятия первый президент Америки входит только один объект (то есть только один человек), а в объем понятия марсианский житель не входит ни одного объекта. Таким образом, по объему понятия бывают общими, единичными и нулевыми, или пустыми.

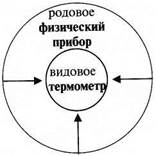
Ограничение понятия – логическая операция перехода от родового понятия к видовому с помощью добавления к его содержанию каких-либо признаков. Например, если к содержанию понятия физический прибор добавить признак «измерять температуру», то это понятие превратится в более узкое по объему понятие – термометр, которое будет видовым по отношению к родовому понятию физический прибор.

 

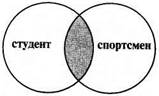
Определение понятия – логическая операция, которая раскрывает содержание понятия. Наиболее распространенный способ определения заключается в том, что определяемое понятие подводится под ближайшее к нему родовое понятие, после чего указывается на его видовое отличие (определение через род и вид), например: Сутки – это часть времени, в течение которого Земля делает полный оборот вокруг своей оси (первая часть определения является подведением определяемого понятия сутки под родовое понятие часть времени, а вторая часть указывает на его видовое отличие от других частей или отрезков времени).

Парадокс – в широком смысле, нечто необычное, нестандартное, удивительное; в логике парадокс – это такая ситуация (необычная и удивительная), когда два противоречащих суждения не только являются одновременно истинными, но еще и вытекают друг из друга.

В отличие от софизма, парадокс это не мыслительная уловка или подвох, который всегда можно разоблачить, а неразрешимое затруднение, мыслительный тупик, «камень преткновения» в логике: за всю ее историю так и не было найдено удовлетворительных и общепризнанных способов преодоления или разрешения парадоксов. Наиболее известным является парадокс лжеца, который заключается в том, что человек говорит: «Я лжец». Анализ этого простого на первый взгляд высказывания приводит к удивительному результату. Любое высказывание, в том числе данное, может быть истинным или ложным. 1. Допустим, что оно истинно, то есть человек сказал правду, но в этом случае он действительно лжец и, произнеся эту фразу, он солгал (получается, что если он сказал правду, то он солгал). 2. Допустим, что высказывание ложно, то есть человек солгал, но в этом случае он не лжец, а правдолюб и, произнеся эту фразу, он сказал правду (получается, что если он солгал, то он сказал правду).

Пересечение – логическое отношение между понятиями, объемы которых совпадают или соприкасаются только в некоторых своих элементах. Например, понятия студент и спортсмен находятся в отношении пересечения, потому что есть такие студенты, которые являются спортсменами, и такие, которые ими не являются; а также есть такие спортсмены, которые являются студентами, и такие, которые ими не являются. На схемах Эйлера это отношение изображается пересекающимися кругами:

 

Подчинение – 1.Логическое отношение между понятиями, объем одного из которых полностью включается в объем другого. Например, понятия карась и рыба находятся в отношении подчинения, так как любой карась является рыбой, но не всякая рыба является карасем. На схемах Эйлера это отношение изображается кругами, один из которых находится внутри другого (меньшее по объему понятие является видовым, а большее – родовым):

 

 

2. Логическое отношение между двумя простыми сравнимыми суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении подчинения, например: Все растения – это живые организмы и Все цветы (некоторые растения) – это живые организмы. Это отношение между простыми суждениями видов А и I, E и О.

Полисиллогизм (или сложный силлогизм) – умозаключение, которое представляет собой два или несколько простых силлогизмов, соединенных между собой таким образом, что вывод одного из них становится посылкой следующего. Например:

 

Понятие – форма мышления, которая обозначает какой-либо объект или его признак и выражается в форме слова или словосочетания, например: человек, птица, небесное тело, знаменитый русский писатель, мужество, красота и т.п.

Понятие видовое – понятие, которое по объему является меньшим по отношению к какому-либо другому понятию – родовому. Например, понятие школа является видовым по отношению к родовому для него понятию учебное заведение (школа – это обязательно учебное заведение, но учебное заведение – это не обязательно школа). Видовые и родовые понятия находятся в отношении подчинения.

Понятие неопределенное – понятие, которое имеет неясное содержание (невозможно точно указать важные отличительные признаки обозначаемого им объекта) и нерезкий объем (невозможно точно установить, включается любой объект в объем этого понятия или не включается в него). Например, понятие хороший шахматист является неопределенным, так как у него неясное содержание (невозможно точно указать признаки хорошего шахматиста, так как представления об этих признаках у разных людей различны) и нерезкий объем (относительно любого человека невозможно точно сказать, является он хорошим шахматистом или нет). Также неопределенными являются понятия умный человек, скучная книга, интересный фильм, престижное учебное заведение, богач, негодяй, старик, толстяк и т.п.

Понятие определенное – понятие, которое имеет ясное содержание (возможно точно указать важные отличительные признаки обозначаемого им объекта) и резкий объем (возможно точно установить, включается любой объект в объем этого понятия или не включается в него). Например, понятие гроссмейстер является определенным, так как у него ясное содержание (возможно точно указать отличительный признак гроссмейстера – «официально обладать соответствующим шахматным титулом») и резкий объем (относительно любого человека можно точно сказать, является он гроссмейстером или нет). Также определенными являются понятия кандидат экономических наук, книга в 500 страниц, цветной кинофильм, высшее учебное заведение и т.п.

Понятие родовое – понятие, которое по объему является большим по отношению к какому-либо другому понятию – видовому. Например, понятие наука является родовым по отношению к видовому для него понятию астрономия (наука – это не обязательно астрономия, но астрономия – это обязательно наука). Родовые и видовые понятия находятся в отношении подчинения.

Посылка – элемент умозаключения, исходное суждение, которое вместе с другими исходными суждениями (посылками) является основанием для выведения нового суждения (заключения). Например:

 

Превращение (или обверсия) – способ преобразования простого суждения, который заключается в том, что его связка меняется с положительной на отрицательную или наоборот. Например, суждение Все караси являются рыбами преобразуется путем превращения в суждение Все караси не являются не рыбами (любое утверждение равно двойному отрицанию). Превращение также считается одним из видов непосредственных умозаключений.

Предикат – элемент простого атрибутивного суждения, обозначающий какой-либо признак или свойство его субъекта, или то, что говорится о субъекте. Например, в суждении Все учебники – это книги понятие учебники является субъектом, а понятие книги – предикатом (в данном суждении об учебниках говорится то, что они книги, или неотъемлемое свойство любого учебника заключается в том, чтобы быть книгой). Предикат обозначается заглавной латинской буквой Р.

Противоположность – см. Контрарность.

Противопоставление предикату – способ преобразования простого суждения, который заключается в том, что сначала это суждение подвергается превращению, а затем – обращению. Например, суждение Все караси являются рыбами преобразуется путем противопоставления предикату следующим образом: 1. Все караси не являются не рыбами (превращение); 2. Все не рыбы (все существа, которые не рыбы) не являются карасями (обращение). Противопоставление предикату также считается одним из видов непосредственных умозаключений.

Противоречие – см. контрадикторность.

Равнозначность – 1. Логическое отношение между понятиями, объемы которых полностью совпадают, например понятия квадрат и равносторонний прямоугольник находятся в отношении равнозначности, потому что любой квадрат является равносторонним прямоугольником, а любой равносторонний прямоугольник является квадратом. На схемах Эйлера это отношение изображается одним кругом, обозначающим полностью совпадающие объемы двух понятий:

 

 

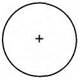
2. Логическое отношение между двумя простыми сравнимыми суждениями, у которых субъекты, предикаты и связки совпадают. Например, суждения Москва является древним городом и Столица России является древним городом находятся в отношении равнозначности.

Распределенность терминов в простом суждении – указатель на количество объектов, охватываемых объемами субъекта и предиката в простом суждении. (Субъект и предикат называются терминами простого суждения.) Термин считается распределенным (развернутым, исчерпанным, взятым в полном объеме), если в суждении речь идет обо всех объектах, входящих в объем этого термина и обозначается знаком «+», а на круговых схемах Эйлера изображается полным кругом:

 

 

Термин считается нераспределенным (неразвернутым, неисчерпанным, взятым не в полном объеме), если в суждении речь идет не обо всех объектах, входящих в этот термин и обозначается знаком «–», а на круговых схемах Эйлера изображается

 

 

Например, в суждении Все сосны ( S) являются деревьями (Р) субъект распределен, а предикат нераспределен, так как в этом суждении речь идет обо всех соснах, но не обо всех деревьях.

 

Силлогизм – дедуктивное умозаключение. Существует несколько видов силлогизмов, которые различаются суждениями, входящими в них в качестве посылок.

1. В простом (категорическом) силлогизме обе посылки и вывод являются простыми суждениями (А, I, E, О), например:

Все небесные тела движутся.

Все планеты – это небесные тела.

Все планеты движутся.

2.В разделительно-категорическом силлогизме первая посылка является разделительным суждением (дизъюнкцией), а вторая посылка является категорическим суждением (простым), например:

Петров учится в 9 классе или в 10 классе, или в 11 классе.

Петров учится в 9 классе.

Петров не учится ни в 10 классе, ни в 11 классе.

 

3. В чисто разделительном силлогизме обе посылки и вывод являются разделительными суждениями (дизъюнкциями), например:

Учебные заведения бывают начальными или средними, или высшими.

Высшие учебные заведения бывают институтами или университетами, или академиями.

Учебные заведения бывают начальными или средними, или институтами, или университетами, или

академиями.

 

4. В условно-категорическом силлогизме первая посылка является условным суждением (импликацией), а вторая посылка является категорическим суждением (простым), например:

Если вещество является металлом, то оно электропроводно.

Железо – это металл.

Железо электропроводно.

 

5. В чисто условном силлогизме обе посылки и вывод являются условными суждениями (импликациями), например:

Если вещество является металлом, то оно электропроводно.

Если вещество электропроводно, то его можно использовать в электроприборах.

Если вещество является металлом, то его можно использовать в электроприборах.

 

6. В эквивалентно-категорическом силлогизме первая посылка является эквивалентным суждением (эквиваленцией), а вторая посылка является категорическим суждением (простым), например:

Если число четное, то оно делится без остатка на 2.

Число 16 – четное.

Число 16 делится без остатка на 2.

 

7. В условно-разделительном силлогизме (см. также Дилемма) первая посылка является условным суждением (импликацией), а вторая посылка является разделительным суждением (дизъюнкцией), например:

Если бы скорость Земли при ее движении вокруг Солнца была больше 42 км/с, то наша планета покинула бы

Солнечную систему, а если бы ее скорость была меньше 3 км/с, то она «упала» бы на Солнце.

Земля не покидает Солнечную систему и (или) не «падает» на Солнце.

Скорость Земли при ее движении вокруг Солнца не больше 42 км/с и (или) не меньше 3 км/с.

Сложение понятий – логическая операция объединения двух (и большего количества) понятий, в результате которой образуется новое понятие, включающее в свой объем все объекты, входящие в объемы исходных понятий. Например, при сложении понятий студент и спортсмен образуется новое понятие, в объем которого входят как все студенты, так и все спортсмены (объем нового понятия или результат сложения на круговых схемах Эйлера изображается штриховкой):

 

Содержание понятия – наиболее важные признаки того объекта, который обозначается этим понятием, например, содержание понятия человек состоит только из одного важного признака – наличие разума, а содержание понятия негр включает в себя два важных признака – 1) наличие разума, 2) цвет кожи; для раскрытия содержания понятия негритянский спортсмен надо указать три важных признака и т.п. Таким образом, по содержанию понятие человек меньше (один признак), чем понятие негр (два признака), а по объему, наоборот, понятие человек шире, чем понятие негр, так как охватывает собой большее количество объектов (людей). Между объемом и содержанием понятия существует обратное отношение: чем больше объем понятия, тем меньше его содержание, и наоборот.

Соподчинение – логическое отношение между понятиями, объемы которых никак не соприкасаются, не имеют общих элементов. Например, понятия береза и сосна находятся в отношении соподчинения, потому что ни одна сосна не является березой и ни одна береза не является сосной. Однако объемы понятий береза и сосна входят в объем более широкого (родового по отношению к ним) понятия дерево, подчиняются ему. На круговых схемах Эйлера отношение соподчинения изображается двумя не соприкасающимися кругами:

 

 

Если понятия обозначают часть и целое, например минута и час, страница книги и книга, колесо автомобиля и автомобиль, то они находятся в отношении соподчинения (минута – это не час, час – это не минута, но и то, и другое – единица времени и т.д.). Если понятия обозначают объекты, слишком далекие друг от друга, чтобы их можно было сравнить, например кирпич и пингвин, то они также могут рассматриваться как соподчиненные: кирпич – это не пингвин, пингвин – это не кирпич, но и то, и другое – форма материи или еще шире – форма бытия, или же просто – нечто существующее.

Сорит – сокращенный полисиллогизм или сложносокращенный силлогизм, в котором пропущена одна из посылок последующего силлогизма, представляющая собой вывод предыдущего. Например:

 

Софизм – внешне правильное и убедительное доказательство какой-либо ложной мысли (идеи) с помощью преднамеренного нарушения логических законов. Например, софизмом является следующее рассуждение: 3 и 4 – это два разных числа, 3 и 4 – это семь, следовательно, семь – это два разных числа. В этом рассуждении смешиваются Две различные вещи: простое перечисление чисел и математическая операция сложения, то есть нарушается логический закон тождества.

Субконтрарность (или частичное совпадение) – логическое отношение между двумя простыми сравнимыми суждениями, в которых объемы субъектов частные, а связки противоположны друг другу, например: Некоторые грибы являются съедобными и Некоторые грибы не являются съедобными. Это отношение между простыми суждениями видов I и О.

Субъект – элемент простого атрибутивного суждения, обозначающий предмет (объект) суждения или то, о чем идет речь в суждении. Например, в суждении Все планеты являются небесными телами речь идет о планетах, поэтому понятие планеты является его субъектом (а понятие небесные тела – предикатом). Субъект суждения обозначается заглавной латинской буквой S.

Суждение – это форма мышления, в которой что-либо утверждается или отрицается (то же, что и высказывание). Суждение состоит из понятий, связанных между собой, выражается в форме предложения, может быть истинным или ложным, простым или сложным (сложное суждение состоит из простых суждений, соединенных каким-либо союзом). Примеры суждений: Все города – это населенные пункты; Некоторые люди являются спортсменами; Ни один кит не является рыбой; Сверкнула молния, и загремел гром; Если вещество металл, то оно элек-тропроводно и т.п.

Суждение атрибутивное (от лат. attributum – признак) – простое суждение, в котором предикат является каким-либо атрибутом (свойством, признаком) субъекта, например: Все тигры – это хищники (в этом суждении предикат является атрибутом или неотъемлемым свойством субъекта: быть хищником – это неотъемлемый или обязательный признак тигра, без которого он не является самим собой). По крупному счету, любое простое суждение можно рассматривать как атрибутивное.

Суждение общеотрицательное – вид простого атрибутивного суждения, которое характеризуется общим объемом субъекта и отрицательной связкой: Все S не есть Р, например: Все киты не являются рыбами. Общеотрицательные суждения обозначаются заглавной латинской буквой Е.

Суждение общеутвердительное – вид простого атрибутивного суждения, которое характеризуется общим объемом субъекта и утвердительной связкой: Все S есть Р, например: Все комары являются насекомыми. Общеутвердительные суждения обозначаются заглавной латинской буквой А.

Суждение релятивное (от лат. relativus – относительный) – простое суждение, в котором выражается какое-то отношение между объектами, например: Иван старше Петра; Эта башня выше той; Москва основана раньше Петербурга; Число 5 больше числа 2 и т.п. Релятивное суждение в принципе можно представить как атрибутивное, в котором предикат указывает на какое-либо отношение к субъекту.

Суждения сравнимые – простые суждения, у которых субъекты и предикаты совпадают, а кванторы и связки различаются. Эти суждения также называются идентичными по материалу. Суждения, у которых субъекты и предикаты различны, являются несравнимыми. Например, суждения Все люди изучали математику и Некоторые люди не изучали математику являются сравнимыми, а суждения Все планеты – это небесные тела и Некоторые рыбы – это акулы являются несравнимыми. Сравнимые суждения могут быть в отношениях равнозначности, подчинения, субконтрарности (частичного совпадения), контрарности (противоположности), контрадикторности (противоречия). Эти отношения изображаются с помощью логического квадрата.

Суждение частноотрицательное – вид простого атрибутивного суждения, которое характеризуется частным объемом субъекта и отрицательной связкой: Некоторые S не есть Р, например: Некоторые животные не являются хищниками. Частноотрицательные суждения обозначаются заглавной латинской буквой О.

Суждение частноутвердительное – вид простого атрибутивного суждения, которое характеризуется частным объемом субъекта и утвердительной связкой: Некоторые S есть Р, например: Некоторые люди являются спортсменами. Частноутвердительные суждения обозначаются заглавной латинской буквой I.

Суждение экзистенциальное (от лат. existentia – существование) – простое суждение, в котором говорится о существовании или не существовании чего-либо (объектов, явлений, свойств и т.п.), например: Бог существует; Чудес не бывает; Счастье есть; Ничего сверхъестественного нет и т.п. Экзистенциальное суждение в принципе можно представить как атрибутивное, в котором предикат указывает на существование или несуществование субъекта.

Теоретический уровень научного познания – второй этап научного познания, на котором путем выдвижения гипотез и их последующего подтверждения и превращения в теории или опровержения и замены новыми гипотезами происходит объяснение фактов, накопленных на первом, эмпирическом уровне, или этапе научного познания.

Умножение понятий – логическая операция объединения двух (и большего количества понятий), в результате которой образуется новое понятие, включающее в свой объем только те объекты, которые являются общими для объемов исходных понятий. Например, при умножении понятий студент и спортсмен образуется новое понятие, в объем которого входят только те студенты, которые являются спортсменами, или, что то же самое, только те спортсмены, которые являются студентами (объем нового понятия или результат умножения на круговых схемах Эйлера изображается штриховкой):