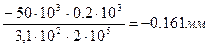Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рекомендуемая последовательность решения задачи 2Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Балку освободить от связей (связи) и их (его) действие заменить силами реакций. 2. Выбрать координатные оси. 3. Составить и решить уравнения равновесия. Реакции опор можно определить, исходя из трех форм уравнений равновесия:
4. Проверить правильность решения задачи. Проверку необходимо производить по тому уравнению равновесия, которое не было использовано при решении данной задачи (задача решена правильно лишь в том случае, если после постановки значений активных и реактивных сил в уравнение равновесия выполняется условие равновесия). 5. Сделать анализ решенной задачи (если при решении задачи реакции опор или реактивный момент получается отрицательным, то их действительное направление противоположно принятому). Пример решения задачи 2. Определение опорных реакций двухопорной балки Определить опорные реакции двухопорной балки в соответствии с рис. 2, если: F1 = 8 кН; F2 = 10 кН; q = 0,4 кН/м; М = 5 кН×м; а = 1,5 м; в = 2 м; с = 2 м. Решение 1. Освобождаем балку от связей (опор), заменив их опорными реакциями. 2. Выбираем расположение координатных осей, совместив ось Х с балкой, а ось У направив перпендикулярно оси Х.
Рисунок 2 3. Составляем уравнения равновесия статики и определяем неизвестные реакции опор. Напомним, что для плоской системы параллельных сил достаточно двух уравнений равновесия åМА= 0; åМВ = 0.
Rв = Rв =
RА = RA = Значение реакции опоры В получено со знаком «минус». Это означает, что RВ направлена вертикально вниз. 4. Проверка правильности найденных результатов å Fку = RА – F1 – q b + F2 + RВ = 0 å Fку = 5,37 – 8 – 0,4 ∙ 2 + 10 – 6,57 = 0 5. Условие равновесия å Fку = 0 выполняется, следовательно, реакции опор RА и RВ найдены верно.
Задачи 3.1 – 3.10 следует решать после изучения тем 1.8, 1.9, 1.10. Для всех задач применяется понятие средней скорости, которая (независимо от вида движения) определяется как результат деления пути, пройденного точкой (или телом) по всей траектории движения, на всё затраченное время. Решая задачи 3.1 – 3.10, рекомендуется разбить весь пройденный путь при движении точки (или тела) на участки равномерного, равноускоренного или равнозамедленного движения в зависимости от условия данной задачи.
Задача 4 может быть решена после усвоения тем 1.5. Прежде чем приступить к её решению, учащийся должен знать формулы определения площадей простых плоских фигур (квадрата, прямоугольника, окружности, прямоугольного треугольника и т.п.) и формулы определения центра тяжести составной плоской фигуры.
Рекомендуемая последовательность решения задания 4 1. В соответствии с заданием начертить чертеж фигуры сложной формы в масштабе МL = 1мм /мм и проставить ее размеры (см. рисунок 3); 2. Провести оси координат так, чтобы они охватывали всю фигуру (если фигура не симметричная, желательно располагать плоскую фигуру в первой четверти системы координатных осей); 3. Разбить сложную фигуру на простые части, определить площадь и координаты центра тяжести каждой простой фигуры относительно выбранной системы координат; 4. Вычислить координаты центра тяжести всей фигуры аналитическим способом. Координаты центра тяжести всей фигуры Х с и Ус определяют по формулам:
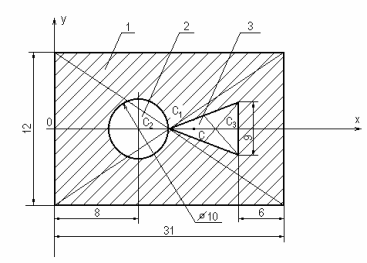
где Х 1, Х 2….Х i - расстояние от оси У до центра тяжести простой фигуры, мм; У 1, У 2….У i - расстояние от оси Х до центра тяжести простой фигуры, мм; А 1, А 2….А i - площадь простой фигуры, мм 2. Если сложная фигура имеет отверстие в виде геометрических фигур, то эти площади необходимо ввести в формулу со знаком «минус». Этот метод называется методом отрицательных площадей. 5. Показать на чертеже центр тяжести плоской фигуры С. Пример решения задания 4 Определить положение центра тяжести сложной плоской фигуры.
Рисунок 3 Решение 1.Проводим систему координат хОу. 2.Сложную фигуру разбить на простые. Ее можно разбить на три простые фигуры: 1 – прямоугольник; 2 – круг; 3 – треугольник. 3.Определение площадей и координат центров тяжести каждой простой фигуры относительно выбранной системы координат; х 1 = А1 = 31× 12 = 372 см2; х 2 = 8 см; у2 = 0; А2 = - знак «минус» показывает, что это площадь отверстия. х 3 = 13 + А3 = - знак «минус» у площади показывает, что это площадь отверстия. 4. Определение координат центров тяжести всей фигуры.
Ответ: Задача 5 может быть решена после усвоения тем 2.1 и 2.2. Прежде чем приступить к её решению, учащийся должен научиться безукоризненно владеть методом сечений для определения внутренних силовых факторов. Эти навыки пригодятся студентам для выполнения всех остальных задач контрольной работы.
Рекомендуемая последовательность решения задания 4 1. Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы и места изменения размеров поперечного сечения. 2. Определить по методу сечений продольную силу для каждого участка (ординаты эпюры Nz), построить эпюру продольных сил Nz. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получaнные значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам. 3. Для построения эпюры нормальных напряжений определить напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т.е. эпюра на данном участке изображать прямой, параллельной оси бруса. 4. Перемещение свободного конца бруса определить как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука. 5. Произвести проверку прочности. Пример решения задачи 5. Для данного стального ступенчатого бруса в соответствии с рисунком 4 построить эпюру продольных сил Дано: F1 = 30 кН; F2 = 38 кН; F3 = 42 кН; А1 = 1,9 см 2; А2 =3,1 см 2 Решение 1. Разбиваем брус на участки 1, 2, 3, 4, 5. 2. Применяя метод сечений, определяем значения продольных сил Nz, Н, на участках бруса
Рисунок 4
Строим эпюру продольных сил N z в соответствии с рисунком 3.1.2. 3. Вычисляем значения нормальных напряжений
Строим эпюру нормальных напряжений в соответствии с рисунком 4. 4. Определяем перемещение свободного конца
Ответ: Брус удлинился на 0,23мм. К решению задачи 6 следует приступать после изучения темы «Кручение».
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 649; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.47.193 (0.007 с.) |






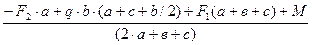



 = 15,5 см; у 1 = 0;
= 15,5 см; у 1 = 0; ; А2 = -
; А2 = -  = - 78,5 см2,
= - 78,5 см2, = 13 + 8 = 21 см; у3 = 0;
= 13 + 8 = 21 см; у3 = 0; = - 54 см2,
= - 54 см2,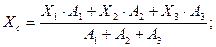
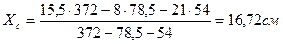 ;
;  .
.
 и нормальных напряжений
и нормальных напряжений  ; определить перемещение свободного конца ∆ℓ.
; определить перемещение свободного конца ∆ℓ.
 , МПа, по формулам:
, МПа, по формулам:





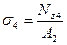



 , мм, по формуле
, мм, по формуле =
=