
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади розв’язування задачСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приклад 9.12. В незатухаючій біжучій хвилі задана точка Розв’язок: Зміщення точки
Щоб знайти початкову фазу Тепер, підставивши числові значення величин
Для знаходження різниці фаз
Цей же результат можна отримати зразу з формули
Таким чином, коливання точки
Приклад 9.13. Для визначення частоти звукових коливань був застосований інтерференційний прилад, зображений на рисунку, де
Розв’язок: В точці
де
При цьому, оскільки переміщення коліна
Враховуючи (3), віднімемо почленно рівняння (2). Тоді одержимо:
Порівнюючи вирази (1) і (2), маємо:
Тепер знайдемо частоту звукових коливань:
Підставивши в формулу числові значення величин, отримаємо:
Приклад 9.14. Мідний стержень довжиною Розв’язок: Якщо будь-якій частинці пружного тіла надати початковий імпульс (наприклад вдарити молотком по торцю стержня), то всі частинки тіла прийдуть в коливальний рух – в тілі встановляться власні коливання. Процес поширення коливань у закріпленому стержні являють собою стоячі хвилі. Ці хвилі є результатом інтерференції двох зустрічних систем біжучих хвиль: падаючих на межу тіла з оточуючим середовищем і відбитих від цієї межі. Частота
Величини Тут по осі З графіка видно, що на всій довжині стержня (від
Звідси
Підставивши це значення
Взявши з таблиць значення
Значення
Приклад 9.15. Джерело
Розв’язок: Биття виникають в результаті додавання коливань з частотами, що мало відрізняються між собою. При цьому частота биттів дорівнює різниці частот коливань, що додаються. З’ясуємо виникнення биттів у даному випадку. Приймача
В той же час джерело звуку наближається до стінки. Тому частоту коливань
Сприймаючи коливання частотою
Приклад 9.16. Від джерела, розташованого біля поверхні Землі, поширюються звукові хвилі. Через який проміжок часу вони досягнуть висоти Розв’язок: Щоб знайти час поширення хвилі, знаючи її переміщення
За умовою задачі температура повітря залежить від висоти. Цю залежність можна записати так:
де
Таким чином, швидкість звуку залежить від висоти. Щоб знайти шуканий час, будемо розглядати рух звукової хвилі як змінний. В такому випадку швидкість в будь-який момент часу дорівнює
Це диференціальне рівняння, що виражає залежність часу від висоти. При зміні часу від
звідки
Підставивши числові значення величин і виконавши обчислення, отримаємо:
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.102.228 (0.011 с.) |

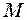 , що знаходиться на відстані
, що знаходиться на відстані  від джерела коливань. Амплітуда коливань
від джерела коливань. Амплітуда коливань 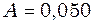 м. Вважаючи, що в початковий момент часу зміщення точки
м. Вважаючи, що в початковий момент часу зміщення точки 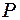 , яка знаходиться в джерелі, максимальне, визначити зміщення від положення рівноваги точки
, яка знаходиться в джерелі, максимальне, визначити зміщення від положення рівноваги точки 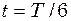 , а також різницю фаз коливань точок
, а також різницю фаз коливань точок 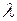 і період
і період 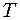 коливань. Враховуючи співвідношення
коливань. Враховуючи співвідношення 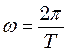 і рівність
і рівність  , одержимо:
, одержимо: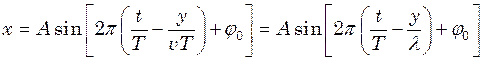 (1)
(1)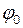 , скористаємося початковими умовами задачі: якщо
, скористаємося початковими умовами задачі: якщо 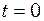 , то
, то  . При цих значеннях
. При цих значеннях 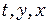 з рівняння (1) маємо
з рівняння (1) маємо  , звідки
, звідки 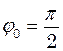 .
.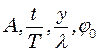 в (1), отримаємо першу відповідь:
в (1), отримаємо першу відповідь: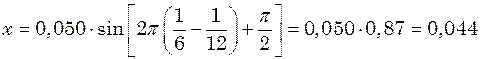 м.
м.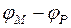 коливань точок
коливань точок  . Отже, в будь-який момент
. Отже, в будь-який момент 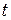 фаза точки
фаза точки 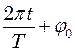 . Тоді:
. Тоді: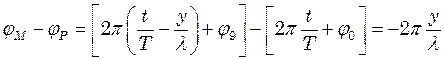 (2)
(2)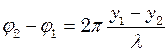 , якщо покласти в ній
, якщо покласти в ній 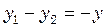 . Підставивши у (2) числове значення відношення
. Підставивши у (2) числове значення відношення 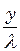 , знайдемо:
, знайдемо: .
.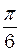 .
.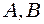 - два коліна, що являють собою порожнисті металеві трубки (коліно
- два коліна, що являють собою порожнисті металеві трубки (коліно 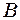 - може висуватися);
- може висуватися);  см. Вважаючи швидкість звуку в повітрі при температурі досліду рівною
см. Вважаючи швидкість звуку в повітрі при температурі досліду рівною 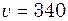 м/с, знайти частоту звукових коливань.
м/с, знайти частоту звукових коливань.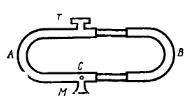
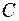 відбувається інтерференція звукових хвиль, що приходять сюди від джерела
відбувається інтерференція звукових хвиль, що приходять сюди від джерела 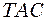 і
і 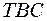 . Результат інтерференції хвиль виражається умовами (32). Перемістивши коліно
. Результат інтерференції хвиль виражається умовами (32). Перемістивши коліно 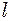 , змінюють тим самим різницю ходу хвиль
, змінюють тим самим різницю ходу хвиль 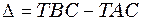 на величину
на величину 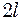 :
: (1)
(1)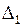 і
і 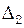 - різниця ходу в початковому і кінцевому положеннях коліна. Оскільки в обох положеннях гучність звуку і пов’язана з нею амплітуда звукових коливань мінімальні, то кожна з величин
- різниця ходу в початковому і кінцевому положеннях коліна. Оскільки в обох положеннях гучність звуку і пов’язана з нею амплітуда звукових коливань мінімальні, то кожна з величин 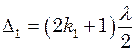 ,
,  (2)
(2)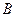 відповідає двом сусіднім мінімумам звуку, повинно виконуватися співвідношення:
відповідає двом сусіднім мінімумам звуку, повинно виконуватися співвідношення: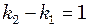 (3)
(3)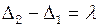 (4)
(4)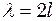
 .
.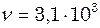 Гц =3,1 кГц.
Гц =3,1 кГц.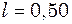 м закріплений у середній частині. Знайти частоти можливих власних поздовжніх коливань стержня.
м закріплений у середній частині. Знайти частоти можливих власних поздовжніх коливань стержня. власних коливань в стержні пов’язана з довжиною
власних коливань в стержні пов’язана з довжиною  поздовжніх хвиль в мідному стержні можна знайти за формулою:
поздовжніх хвиль в мідному стержні можна знайти за формулою: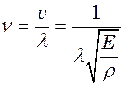 .
.
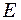 ,
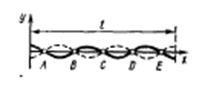
, 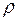 для міді табличні, і наша задача зводиться до визначення довжин хвиль, що відповідають власним коливанням стержня. Цим коливанням завжди відповідає такий розподіл по довжині тіла стоячих хвиль, які задовольняють граничним умовам: на закріпленому кінці тіла повинен бути вузол зміщень, на вільному – пучність. Отже, на кінцях даного стержня повинні бути пучності зміщень, а посередині його – вузол зміщень, оскільки в цьому місці стержень закріплений. Один з можливих варіантів розподілу стоячих хвиль по довжині стержня зображений на рис. 9.6.
для міді табличні, і наша задача зводиться до визначення довжин хвиль, що відповідають власним коливанням стержня. Цим коливанням завжди відповідає такий розподіл по довжині тіла стоячих хвиль, які задовольняють граничним умовам: на закріпленому кінці тіла повинен бути вузол зміщень, на вільному – пучність. Отже, на кінцях даного стержня повинні бути пучності зміщень, а посередині його – вузол зміщень, оскільки в цьому місці стержень закріплений. Один з можливих варіантів розподілу стоячих хвиль по довжині стержня зображений на рис. 9.6. відкладені відстані точок стержня від його лівого кінця, по осі
відкладені відстані точок стержня від його лівого кінця, по осі 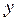 - зміщення точок стержня від положення рівноваги, які вони мають в деякий момент часу, беручи участь в поздовжніх коливаннях (пунктиром зображений графік зміщення через проміжок часу
- зміщення точок стержня від положення рівноваги, які вони мають в деякий момент часу, беручи участь в поздовжніх коливаннях (пунктиром зображений графік зміщення через проміжок часу  ). Точки
). Точки 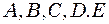 - вузли стоячої хвилі.
- вузли стоячої хвилі. до
до 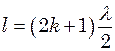 ,
, 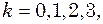 ….
….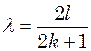
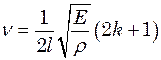 .
. Н/м2,
Н/м2, 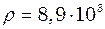 кг/м3 і виконавши обчислення, знайдемо:
кг/м3 і виконавши обчислення, знайдемо: Гц.
Гц.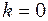 дає основну частоту власних коливань
дає основну частоту власних коливань 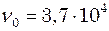 Гц. Значення
Гц. Значення 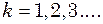 відповідають вищим гармонічним частотам.
відповідають вищим гармонічним частотам.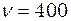 Гц рухається зі швидкістю
Гц рухається зі швидкістю 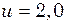 м/с, віддаляючись від нерухомого приймача
м/с, віддаляючись від нерухомого приймача 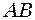 . Визначити частоту биттів, які реєструються приймачем звуку. Швидкість звуку
. Визначити частоту биттів, які реєструються приймачем звуку. Швидкість звуку 
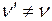 . Поклавши в формулу (35)
. Поклавши в формулу (35) 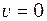 і враховуючи, що, згідно правила знаків,
і враховуючи, що, згідно правила знаків, 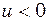 , оскільки джерело віддаляється від приймача, отримаємо
, оскільки джерело віддаляється від приймача, отримаємо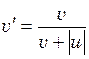 (1)
(1) , що сприймається стінкою, знайдемо знову за формулою (35), де
, що сприймається стінкою, знайдемо знову за формулою (35), де  , отже:
, отже: (2)
(2)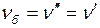 знайдемо, використовуючи формули (1),(2):
знайдемо, використовуючи формули (1),(2):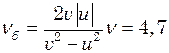 Гц.
Гц. км, якщо температура повітря біля поверхні Землі
км, якщо температура повітря біля поверхні Землі 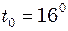 С, а градієнт температури в атмосфері
С, а градієнт температури в атмосфері 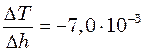 К/м.
К/м. , з’ясуємо спочатку, яка швидкість звуку у вертикальному напрямі. Швидкість звуку в повітрі визначається формулою (37), де
, з’ясуємо спочатку, яка швидкість звуку у вертикальному напрямі. Швидкість звуку в повітрі визначається формулою (37), де 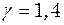 . Можна показати, що при цьому швидкість залежить від температури повітря. Дійсно, оскільки
. Можна показати, що при цьому швидкість залежить від температури повітря. Дійсно, оскільки  , то, застосувавши рівняння газового стану, отримаємо
, то, застосувавши рівняння газового стану, отримаємо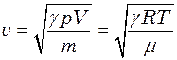 (1)
(1)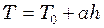 (2)
(2)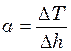 - градієнт температури, що показує приріст (в даному випадку від’ємний) температури на кожний метр висоти. Підставивши значення
- градієнт температури, що показує приріст (в даному випадку від’ємний) температури на кожний метр висоти. Підставивши значення  (3)
(3)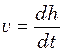 , звідки з урахуванням формули (3)
, звідки з урахуванням формули (3)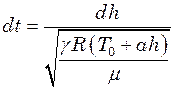
 до
до 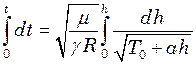 ,
,
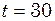 с.
с.


