
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оператор інтегрування: застосування, пояснення, приклади.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оператор інтегрування, визначений інтеграл Інтегрування, диференціювання, як і безліч інших математичних дій, влаштоване в Mathcad за принципом "як пишеться, так і вводиться". Щоб обчислити визначений інтеграл, варто надрукувати його звичайну математичну форму в документі. Робиться це за допомогою панелі Calculus (Обчислення) натисканням кнопки зі значком інтеграла чи введенням із клавіатури сполучення клавіш <Shift>+<7> (чи символу "&", що те ж саме). З'явиться символ інтеграла з декількома покажчиками (мал. 6.1), у які потрібно ввести нижній і верхній інтервали інтегрування, підінтегральну функцію і змінну інтегрування. Можна обчислювати інтеграли з одним чи обома нескінченними межами. Для цього на місці відповідної межі введіть символ нескінченності, скориставшись, наприклад, тією ж самою панеллю Calculus. Щоб ввести - (мінус нескінченність), додайте знак мінус до символу нескінченності, як до звичайного числа.
Мал. 6.1. Вставка оператора визначеного інтеграла Щоб отримати результат інтегрування, варто ввести знак рівності чи символьної рівності. У першому випадку інтегрування буде проведено чисельним методом, у другому випадку буде знайдено точне значення інтеграла за допомогою символьного процесора Mathcad. Ці два способи ілюструє приклад 6.1. Звичайно, символьне інтегрування можливе тільки для невеликого кола нескладних підінтегральних функцій.
Приклад 6.1 Чисельне і символьне обчислення визначеного інтеграла Оператор інтегрування може використовуватися так само, як і інші оператори: для визначення функцій, в циклах і при обчисленні ранжованих змінних. Приклад використання визначеного інтеграла у функції користувача g(α) і обчислення декількох її значень для ранжованої змінної наведено в прикладі 6.2.
Приклад 6.2 Чисельне і символьне обчислення визначеного інтеграла Підінтегральна функція може залежати від будь-якої кількості змінних. Для обчислення інтеграла потрібно вказати, за якою змінною Mathcad слід обчислювати інтеграл. Цю змінну потрібно ввести у відповідний покажчик. Слід пам'ятати, що для чисельного інтегрування за однією із змінних заздалегідь слід задати значення решти змінних, від яких залежить підінтегральна функція (приклад 6.2).
Приклад 6.3 Інтегрування функції двох змінних за різними змінними Дійсні та комплексні числа: призначення, застосування і приклади. Дійсні числа Будь-який вираз, що починається з цифри, Mathcad інтерпретує як число. Тому для введення числа потрібно його просто набрати на клавіатурі. Mathcad зберігає всі числа в однаковому форматі, але вводити їх можна в найбільш зручному вигляді (notation), виходячи з контексту документа: - як ціле число; - як десяткове число (decimal notation) з будь-якою кількістю десяткових цифр після крапки; - у представленні з порядком (exponential notation). В цьому випадку після введення числа потрібно надрукувати символ множення і ввести 10 у потрібному ступені; - як число в іншій системі числення (. двійковій (binary), восьмиричній (octal) або шістнадцятирічній (hexadecimal).
Приклад 3.1. Введення дійсних чисел Комплексні числа Більшість операцій у середовищі Mathcad за замовчуванням здійснюється над комплексними числами. Комплексне число є сумою дійсного й уявного числа, щовиходить шляхом множення будь-якого дійсного числа на уявну одиницю (imaginary unit) i. За визначенням, i =
Мал.3.1 Введення уявної одиниці
Приклад 3.2. Комплексні числа Для роботи з комплексними числами є кілька простих функцій і операторів (Див. приклад 3.3). Базові з них: Re(z) - дійсна частина комплексного числа z; im(z) - уявна частина комплексного числа z; arg(z) - аргумент комплексного числа z;
Приклад 3.3. Базові функції роботи з комплексними числами
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.72.233 (0.011 с.) |







 або
або  . Комплексне число можна ввести у вигляді звичайної суми дійсної і уявної частин, чи у вигляді будь-якого виразу, що містить уявне число. Уявну одиницю можна позначити символом і або j. Щоб ввести уявну одиницю потрібно натиснути клавіші <1>та <i>. Якщо просто ввести символ "i", то Mathcad інтерпретує його як змінну i. Крім того, уявна одиниця має вигляд 1i тільки тоді, якщо відповідна формула виокремлена. В протилежному випадку уявна одиниця відображається просто як символ i (Мал.3.1). Введення і виведення комплексних чисел ілюструється прикладом 3.2.
. Комплексне число можна ввести у вигляді звичайної суми дійсної і уявної частин, чи у вигляді будь-якого виразу, що містить уявне число. Уявну одиницю можна позначити символом і або j. Щоб ввести уявну одиницю потрібно натиснути клавіші <1>та <i>. Якщо просто ввести символ "i", то Mathcad інтерпретує його як змінну i. Крім того, уявна одиниця має вигляд 1i тільки тоді, якщо відповідна формула виокремлена. В протилежному випадку уявна одиниця відображається просто як символ i (Мал.3.1). Введення і виведення комплексних чисел ілюструється прикладом 3.2.
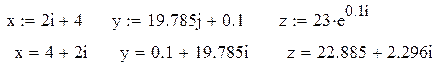
 - модуль комплексного числа z;
- модуль комплексного числа z;



