
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні поняття і співвідношенняСодержание книги
Поиск на нашем сайте
ТЕМА 9 КОЛИВАННЯ І ХВИЛІ Основні поняття і співвідношення Механічні коливання Рівняння гармонічних коливань
Швидкість і прискорення точки, що здійснює гармонічні коливання:
Сила, що діє на матеріальну точку масою
Кінетична енергія точки, що здійснює прямолінійні гармонічні коливання
Потенціальна енергія точки, яка здійснює гармонічні коливання під дією пружної сили
Механічна енергія:
Диференціальне рівняння гармонічних коливань матеріальної точки масою
Розв’язок цього рівняння
Період коливань математичного маятника
Період коливань пружинного маятника:
Період коливань фізичного маятника:
Амплітуда результуючого коливання, що одержується при додаванні двох гармонічних коливань однакового напрямку і однакової частоти:
Початкова фаза результуючого коливання:
Період биття:
Рівняння траєкторії руху точки, що бере участь у двох взаємно перпендикулярних коливаннях однакової частоти (рівняння еліпса):
Диференціальне рівняння вільних згасаючих коливань і його розв’язок:
Декремент згасання
Логарифмічний декремент згасання
Добротність коливної системи:
Диференціальне рівняння вимушених механічних коливань і його розв’язок для усталених коливань
Резонансна частота і амплітуда
Пружні хвилі Зв'язок між довжиною хвилі
Хвильове число
Рівняння плоскої хвилі, що поширюється вздовж додатного напрямку осі
Рівняння сферичної хвилі
Хвильове рівняння
Хвильове рівняння для плоскої хвилі, що поширюється вздовж осі
Фазова
Зв'язок між різницею фаз
Умови максимуму і мінімуму амплітуди при інтерференції хвиль
Рівняння стоячої хвилі
Координати пучностей і вузлів стоячої хвилі
Ефект Допплера в акустиці
Швидкість поздовжніх хвиль в тонких стержнях:
Швидкість звуку в газах:
Амплітуда звукового тиску
Інтенсивність звуку
Рівень інтенсивності звуку (в децибелах) визначається формулою
Рівень гучності звуку (в фонах) обчислюється за формулою
І РІВЕНЬ 9.1.1. Написати рівняння гармонічного коливання з амплітудою 9.1.2. Написати рівняння гармонічного коливання з амплітудою 9.1.3. За який час від початку руху точка, що здійснює коливальний рух за рівнянням 9.1.4. Амплітуда гармонічного коливання 9.1.5. Рівняння коливань матеріальної точки масою 9.1.6. Знайти відношення кінетичної енергії точки, що здійснює гармонічні коливання, до її потенціальної енергії для моментів часу 9.1.7. До пружини підвішений вантаж масою 9.1.8. До пружини підвішений вантаж. Максимальна кінетична енергія коливань вантажу 9.1.9. Як зміниться період вертикальних коливань вантажу, що висить на двох пружинах, якщо від послідовного з’єднання пружин перейти до паралельного їх з’єднання? 9.1.10. Написати рівняння руху, що одержується в результаті додавання двох однаково напрямлених гармонічних коливань з однаковим періодом 9.1.11. Знайти амплітуду 9.1.12. Знайти амплітуду 9.1.13. написати рівняння результуючого коливання, що отримується в результаті додавання двох взаємно перпендикулярних коливань з однаковою частотою
9.1.14. Точка приймає участь в двох коливаннях однакового періоду з однаковими початковими фазами. Амплітуди коливань рівні а) в одному напрямку; б) в двох взаємно перпендикулярних напрямках. 9.1.15. Точка бере участь в двох взаємно перпендикулярних коливаннях 9.1.16. Період згасаючих коливань 9.1.17. Логарифмічний декремент згасання математичного маятника 9.1.18. Тіло масою 9.1.19. По ґрунтовій дорозі пройшов трактор, залишивши сліди у вигляді ряду заглибин, що знаходяться на відстані 9.1.20. Знайти довжину хвилі 9.1.21. Звукові коливання, що мають частоту 9.1.22. Рівняння незгасаючих коливань має вигляд 9.1.23. Знайти положення вузлів і пучностей і накреслити графік стоячої хвилі, якщо: а) відбивання відбувається від менш густого середовища; б) відбивання відбувається від більш густого середовища. Довжина біжучої хвилі 9.1.24. Знайти швидкість поширення звуку в сталі. 9.1.25. За допомогою ехолота вимірювалась глибина моря. Якою була ця глибина, якщо проміжок часу між виникненням звуку і його прийомом рівний
ІІ РІВЕНЬ 9.2.1. Сталева смужка затиснута з одного кінця і розташована горизонтально. На другому кінці смужки закріплюють вантаж, маса якого значно більша за масу смужки. При наявності вантажу смужка прогинається і її не затиснутий кінець опускається на 4 см. 1) З якою частотою буде коливатися вантаж, якщо його штовхнути у вертикальному напрямі? 2) З яким прискоренням буде рухатись вантаж, що коливається, в момент, коли смужка повністю розпрямиться? 9.2.2. На верхню вітку горизонтально розташованого камертона насипаний дрібний пісок, рис. 9.8. З допомогою смичка камертон приводять у коливний рух. Частота коливань камертона
а) яка амплітуда коливань в тих місцях вітки камертона, де піщинки не підскакують? б) Яка амплітуда коливань в тих місцях, де піщинки підскакують на висоту
9.2.3. При рівновазі системи, показаній на рис. 9.9, пружина П розтягнута на 9.2.4. Верхній кінець сталевої дротини діаметром 0,5 мм і довжиною 80 см закріплений. До нижнього кінця дротини прикріплено кулю масою 2 кг і діаметром 10 см. Якщо кулю повернути навколо вертикальної осі на невеликий кут і відпустити, він буде здійснювати крутильні коливання. Визначте період коливань кулі. а) Визначте період коливань однорідної кулі радіуса 6 см навколо горизонтальної осі, що проходить через точку, що знаходиться на відстані 0,3 радіуса кулі від її центра; б) Яким буде період коливань, якщо розташувати вісь під кутом 800 до горизонту. 9.2.5. Тонка прямокутна пластинка може коливатися навколо горизонтальної осі, що лежить в її площині і перпендикулярна до однієї з її сторін, довжина якої дорівнює а) Який період коливань, якщо вісь співпадає з верхньою стороною пластинки? б) При якій відстані від осі до середини пластинки період коливань буде найменшим? Який цей період?
9.2.6. Визначте період коливань ртуті масою 9.2.7. Початкова амплітуда коливань маятника рівна 3 см. Через 10 с вона стала рівною 1 см. Через скільки часу амплітуда коливань буде рівна 0,3 см? 9.2.8. Який логарифмічний декремент згасання маятника довжиною 0,8 м, якщо його початкова амплітуда рівна 50, а через 5 хв. вона стає рівною 0,50? 9.2.9. Пружне тіло коливається в середовищі, причому логарифмічний декремент згасанні рівний 0,7. 1) Чи можливі згасаючі коливання цього тіла в середовищі, коефіцієнт опору якого в 10 разів більший, ніж у даного середовища? 2) Дайте відповідь на це саме питання, якщо декремент згасання в даному середовищі дорівнює 0,6; 0,1. 3) Якщо коливання в більш в’язкому середовищі можливі, то які їх декременти згасання?
9.2.10. Амплітуди швидкостей вимушених коливань при частотах вимушуючої сили 9.2.11. Амплітуди зміщень вимушених коливань при частотах вимушуючої сили 9.2.12. Амплітуда зміщення вимушених коливань при дуже малій частоті дорівнює 9.2.13. Швидкість поздовжніх пружних хвиль в сталевому стержні дорівнює 5100 м/с. Визначте модуль пружності сталі. 9.2.14. Яка швидкість поздовжніх пружних хвиль в ртуті? 9.2.15. Визначте частоти коливань для стоячих звукових хвиль в трубі довжиною 80 см: 1) відкритій; 2) закритій. Температура повітря в трубі 160С. 9.2.16. На нитці утворилися стоячі хвилі, причому відстань між точками, в яких коливання відбуваються з амплітудою 3 мм, дорівнює 3 і 7 см. Знайдіть довжину хвилі і амплітуду в середині пучності. 9.2.17. Частота основного тону гудка електровоза 650 Гц. Якої частоти сприйме гудок нерухомий спостерігач, до якого електровоз наближається зв швидкість 54 км/год? Температура повітря 160С. 9.2.18. Спостерігачу, що слухає гудок автомобіля, здається, що при наближенні автомобіля частота основного тону гудка більша в 9.2.19. Дайте відповідь на те саме запитання, якщо автомобіль, що гудить, нерухомий, а спостерігач знаходиться в автомобілі, який спочатку наближається, а потім віддаляється від автомобіля, що гудить.
ІІІ РІВЕНЬ 9.3.1. Точка здійснює гармонічні коливання по закону 9.3.2. Частинка здійснює гармонічні коливання вздовж осі 9.3.3. Методом векторних діаграм знайти амплітуду а) б) 9.3.4. Точка рухається в площині а) рівняння траєкторії точки
б) прискорення 9.3.5. Знайти рівняння траєкторії а) б) Зобразити приблизні графіки цих траєкторій. 9.3.6. Частинка масою 9.3.7. Два математичних маятники, довжина кожного 9.3.8. Однорідний стержень довжиною
9.3.9. Математичний маятник довжиною 9.3.10. Тонке кільце радіуса а) в площині рисунка; б) в напрямку, перпендикулярному до площини рисунка.
9.3.11. В системі на рисунку 9.3.12. Згасаючі коливання точки відбуваються за законом а) амплітуду зменшення і швидкість точки в момент б) моменти, коли точка досягає крайніх положень. 9.3.13. Тіло здійснює крутильні коливання за законом а) кутову швидкість б) моменти, коли кутова швидкість максимальна. 9.3.14. Математичний маятник здійснює коливання в середовищі, для якого логарифмічний декремент згасання 9.3.15. До пружини підвісили вантаж, і вона розтягнулася на 9.3.16. Кулька масою 9.3.17. При частотах вимушуючої гармонічної сили а) частоту, що відповідає резонансу швидкості; б) коефіцієнт згасання 9.3.18. За скільки часу звукові коливання пройдуть відстань
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.240.14 (0.012 с.) |

 , (9.1)
, (9.1) - зміщення частинки, що коливається, від положення рівноваги;
- зміщення частинки, що коливається, від положення рівноваги;  - амплітуда коливань;
- амплітуда коливань;  - колова (циклічна) частота;
- колова (циклічна) частота;  - частота;
- частота; 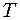 - період коливань;
- період коливань; 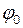 - початкова фаза.
- початкова фаза. , (9.2)
, (9.2)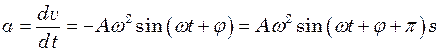 , (9.3)
, (9.3)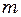 , яка здійснює коливання:
, яка здійснює коливання: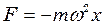 , (9.4)
, (9.4) (9.5)
(9.5) :
: (9.6)
(9.6) . (9.7)
. (9.7) або
або 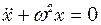 , (9.8)
, (9.8)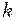 - коефіцієнт пружності;
- коефіцієнт пружності; 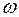 - циклічна частота.
- циклічна частота.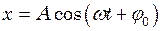 . (9.9)
. (9.9) , (9.10)
, (9.10)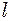 - довжина маятника;
- довжина маятника;  - прискорення вільного падіння.
- прискорення вільного падіння. , (9.11)
, (9.11) , (9.12)
, (9.12) - момент інерції маятника відносно осі коливань;
- момент інерції маятника відносно осі коливань;  - зведена довжина фізичного маятника;
- зведена довжина фізичного маятника;  . (9.13)
. (9.13) , (9.14)
, (9.14) і
і  - амплітуди двох коливань, що додаються;
- амплітуди двох коливань, що додаються;  і
і 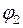 - початкові фази коливань.
- початкові фази коливань. , (9.15)
, (9.15) - різниця частот коливань, що додаються
- різниця частот коливань, що додаються 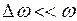 .
. (9.16)
(9.16)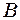 - амплітуди коливань, що додаються;
- амплітуди коливань, що додаються;  - різниця фаз обох коливань.
- різниця фаз обох коливань.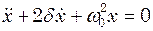 ,
,  (9.17)
(9.17) - коефіцієнт згасання;
- коефіцієнт згасання;  - власна частота коливної системи;
- власна частота коливної системи;  - частота згасаючих коливань;
- частота згасаючих коливань;  - амплітуда згасаючих коливань.
- амплітуда згасаючих коливань. (9.18)
(9.18) і
і  - амплітуди двох послідовних коливань, що відрізняються на період.
- амплітуди двох послідовних коливань, що відрізняються на період. (9.19)
(9.19) - коефіцієнт згасання;
- коефіцієнт згасання;  - час релаксації;
- час релаксації; 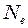 - число коливань, що здійснюються за час зменшення амплітуди в
- число коливань, що здійснюються за час зменшення амплітуди в  разів.
разів. (9.20)
(9.20)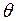 - логарифмічний декремент згасання;
- логарифмічний декремент згасання; 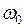 - циклічна частота вільних незгасаючих коливань тієї ж коливної системи;
- циклічна частота вільних незгасаючих коливань тієї ж коливної системи;  ,
,  (9.21)
(9.21) - амплітуда вимушуючої сили;
- амплітуда вимушуючої сили;  ,
,  (9.22)
(9.22) ,
,  (9.23)
(9.23)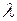 , періодом
, періодом 
 ,
,  (9.24)
(9.24) - швидкість поширення коливань в середовищі (фазова швидкість)
- швидкість поширення коливань в середовищі (фазова швидкість) (9.25)
(9.25)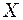 :
: (9.26)
(9.26) - зміщення точок середовища з координатою
- зміщення точок середовища з координатою 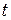 ;
;  - хвильове число;
- хвильове число;  (9.27)
(9.27) - зміщення точок середовища на відстані
- зміщення точок середовища на відстані  від центра хвилі в момент часу
від центра хвилі в момент часу  - стала величина;
- стала величина;  (9.28)
(9.28) - оператор Лапласа;
- оператор Лапласа; 
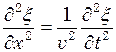 (9.29)
(9.29) швидкості і зв'язок між ними:
швидкості і зв'язок між ними: ;
;  ;
;  (9.30)
(9.30)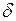 і різницею ходу хвиль
і різницею ходу хвиль  :
: (9.31)
(9.31) ,
,  (9.32)
(9.32)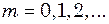 ;
;  . (9.33)
. (9.33) ,
, 
 (9.34)
(9.34) (9.35)
(9.35)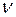 - частота звуку, що сприймається рухомим приймачем;
- частота звуку, що сприймається рухомим приймачем; 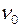 - частота звуку, що посилається джерелом;
- частота звуку, що посилається джерелом;  - швидкість руху приймача;
- швидкість руху приймача;  - швидкість руху джерела;
- швидкість руху джерела;  (9.36)
(9.36)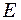 - модуль пружності,
- модуль пружності, 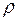 - густина матеріалу стержня.
- густина матеріалу стержня. (9.37)
(9.37) і
і  - відношення теплоємності газу при сталому тиску до теплоємності при сталому об’ємі.
- відношення теплоємності газу при сталому тиску до теплоємності при сталому об’ємі. і амплітуда швидкості
і амплітуда швидкості  частинок у звуковій хвилі пов’язані співвідношенням:
частинок у звуковій хвилі пов’язані співвідношенням: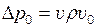 (9.38)
(9.38) , тобто енергія, що переноситься звуковою хвилею за одиницю часу через одиничну площадку, перпендикулярну напрямку поширення хвилі, виражається через амплітуду звукового тиску:
, тобто енергія, що переноситься звуковою хвилею за одиницю часу через одиничну площадку, перпендикулярну напрямку поширення хвилі, виражається через амплітуду звукового тиску: (9.39)
(9.39) (9.40)
(9.40)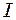 - інтенсивність даного звуку;
- інтенсивність даного звуку;  Вт/м2 – інтенсивність звуку на порозі чутності при стандартній частоті
Вт/м2 – інтенсивність звуку на порозі чутності при стандартній частоті  Гц.
Гц.
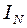 - інтенсивність звуку частоти
- інтенсивність звуку частоти 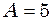 см, якщо за час
см, якщо за час 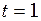 хв. здійснюється 150 коливань і початкова фаза коливань
хв. здійснюється 150 коливань і початкова фаза коливань 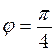 . Накреслити графік.
. Накреслити графік.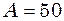 мм, періодом
мм, періодом 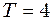 с і початковою фазою
с і початковою фазою 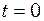 і
і 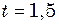 с. Накреслити графік.
с. Накреслити графік. проходить шлях від положення рівноваги до максимального зміщення?
проходить шлях від положення рівноваги до максимального зміщення?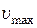 точки, що коливається, і її максимальне прискорення
точки, що коливається, і її максимальне прискорення 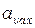 .
.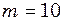 г має вигляд
г має вигляд 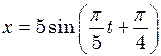 см. Знайти максимальну силу
см. Знайти максимальну силу 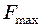 , що діє на точку, і повну енергію
, що діє на точку, і повну енергію 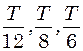 . Початкова фаза коливань
. Початкова фаза коливань 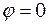 .
.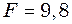 Н розтягується на
Н розтягується на 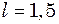 см, знайти період
см, знайти період 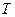 вертикальних коливань вантажу.
вертикальних коливань вантажу.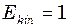 Дж. Амплітуда коливань
Дж. Амплітуда коливань 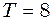 с і однаковою амплітудою
с і однаковою амплітудою 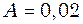 м. Початкова фаза одного з цих коливань рівна нулю.
м. Початкова фаза одного з цих коливань рівна нулю.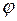 гармонічного коливання, отриманого від додавання однаково напрямлених коливань, заданих рівняннями
гармонічного коливання, отриманого від додавання однаково напрямлених коливань, заданих рівняннями 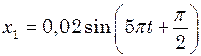 і
і 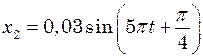 .
.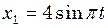 і
і 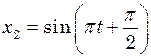 . Написати рівняння результуючого коливання. Дати векторну діаграму додавання коливань.
. Написати рівняння результуючого коливання. Дати векторну діаграму додавання коливань.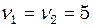 Гц і однаковою початковою фазою
Гц і однаковою початковою фазою 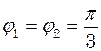 . Амплітуди коливань рівні
. Амплітуди коливань рівні  м і
м і 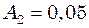 м.
м. і
і 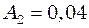 м. Знайти амплітуду результуючого коливання, якщо коливання здійснюються
м. Знайти амплітуду результуючого коливання, якщо коливання здійснюються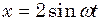 і
і 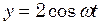 . Знайти траєкторію результуючого руху точки.
. Знайти траєкторію результуючого руху точки.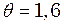 ; початкова фаза
; початкова фаза 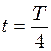 зміщення точки
зміщення точки 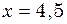 см. Написати рівняння руху цього коливання. Побудувати графік цього коливання в межах двох періодів.
см. Написати рівняння руху цього коливання. Побудувати графік цього коливання в межах двох періодів.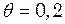 . У скільки разів зменшиться амплітуда коливань за одне повне коливання маятника?
. У скільки разів зменшиться амплітуда коливань за одне повне коливання маятника?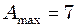 см, початковою фазою
см, початковою фазою 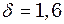 с-1. На це тіло почала діяти зовнішня періодична сила
с-1. На це тіло почала діяти зовнішня періодична сила 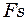 , під дією якої встановилися вимушені коливання. Рівняння вимушених коливань має вигляд
, під дією якої встановилися вимушені коливання. Рівняння вимушених коливань має вигляд 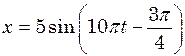 . Знайти (з числовими коефіцієнтами) рівняння власних коливань і рівняння зовнішньої періодичної сили.
. Знайти (з числовими коефіцієнтами) рівняння власних коливань і рівняння зовнішньої періодичної сили.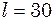 см один від одної. По цій дорозі прокотили дитячу коляску, що має дві однакові ресори, кожна з яких прогинається на
см один від одної. По цій дорозі прокотили дитячу коляску, що має дві однакові ресори, кожна з яких прогинається на 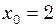 см під дією вантажу масою
см під дією вантажу масою 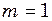 кг. З якою швидкістю
кг. З якою швидкістю 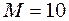 кг.
кг.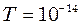 с. Швидкість поширення коливань
с. Швидкість поширення коливань 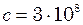 м/с.
м/с.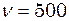 Гц і амплітуду
Гц і амплітуду 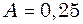 мм, поширюються в повітрі. Довжина хвилі
мм, поширюються в повітрі. Довжина хвилі 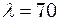 см. Знайти швидкість
см. Знайти швидкість 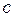 поширення коливань і максимальну швидкість
поширення коливань і максимальну швидкість 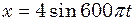 см. Знайти зміщення
см. Знайти зміщення 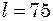 см від джерела коливань, для моменту часу
см від джерела коливань, для моменту часу 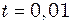 с після початку коливань. Швидкість поширення коливань
с після початку коливань. Швидкість поширення коливань 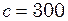 м/с.
м/с.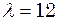 см.
см.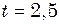 с. Стисливість води
с. Стисливість води 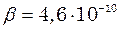 Па, густина морської води
Па, густина морської води 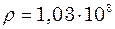 кг/м3.
кг/м3.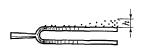
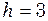 мм (по відношенню до положення у випадку камертона в стані спокою), вважаючи удар піщинки об камертон непружним?
мм (по відношенню до положення у випадку камертона в стані спокою), вважаючи удар піщинки об камертон непружним?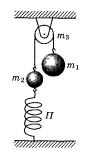
 см порівняно з не деформованим станом. Блок являє собою суцільний однорідний диск. Маси вантажів і блока відповідно дорівнюють
см порівняно з не деформованим станом. Блок являє собою суцільний однорідний диск. Маси вантажів і блока відповідно дорівнюють 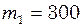 г,
г, 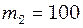 г,
г, 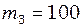 г. Іншими масами і тертям можна знехтувати. Визначити період коливань системи, які почнуться, якщо вантаж
г. Іншими масами і тертям можна знехтувати. Визначити період коливань системи, які почнуться, якщо вантаж 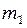 відвести вертикально вниз і відпустити.
відвести вертикально вниз і відпустити.
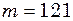 г, що знаходиться в
г, що знаходиться в 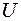 − подібній трубці, рис. 9.10. Площа перерізу каналу трубки
− подібній трубці, рис. 9.10. Площа перерізу каналу трубки 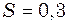 см2.
см2.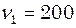 Гц і
Гц і 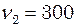 Гц однакові. Приймаючи, що амплітуда вимушуючої сили в обох випадках одна і та сама, знайдіть частоту, що відповідає резонансу швидкостей.
Гц однакові. Приймаючи, що амплітуда вимушуючої сили в обох випадках одна і та сама, знайдіть частоту, що відповідає резонансу швидкостей.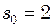 мм, а при резонансі рівна
мм, а при резонансі рівна 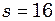 мм. Припускаючи, що декремент згасання менший за одиницю, визначте його.
мм. Припускаючи, що декремент згасання менший за одиницю, визначте його.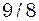 рази, ніж при віддаленні. Визначте швидкість автомобіля, прийнявши швидкість звуку в повітрі рівною 340 м/с. Вважати повітря нерухомим.
рази, ніж при віддаленні. Визначте швидкість автомобіля, прийнявши швидкість звуку в повітрі рівною 340 м/с. Вважати повітря нерухомим.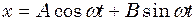 , де
, де 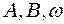 - сталі. Знайти амплітуду
- сталі. Знайти амплітуду 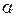 цих коливань.
цих коливань.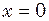 . Частота коливань
. Частота коливань 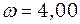 с-1. В деякий момент координата частинки
с-1. В деякий момент координата частинки 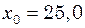 см і її швидкість
см і її швидкість 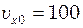 см/с. Знайти координату
см/с. Знайти координату 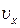 частинки через
частинки через 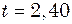 с після цього моменту.
с після цього моменту.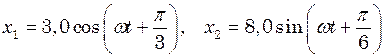 ;
;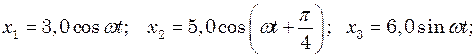
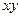 за законом
за законом 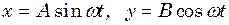 , де
, де 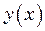 і напрям її руху по цій траєкторії;
і напрям її руху по цій траєкторії;
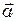 точки в залежності від її радіуса-вектора
точки в залежності від її радіуса-вектора 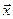 відносно початку координат.
відносно початку координат.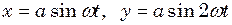 ;
;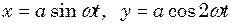 .
.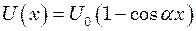 ,
, 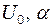 - сталі. Знайти період малих коливань частинки навколо положення рівноваги.
- сталі. Знайти період малих коливань частинки навколо положення рівноваги.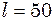 см і маса
см і маса 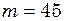 г, з’єднані пружинкою жорсткістю
г, з’єднані пружинкою жорсткістю 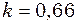 Н/м, рис. 9.11. При рівновазі маятники займають вертикальне положення. Знайти період малих коливань цих маятників, якщо їх коливання відбуваються у вертикальній площині в протилежні боки (у протифазі).
Н/м, рис. 9.11. При рівновазі маятники займають вертикальне положення. Знайти період малих коливань цих маятників, якщо їх коливання відбуваються у вертикальній площині в протилежні боки (у протифазі).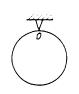
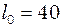 см і тонкий однорідний стержень довжиною
см і тонкий однорідний стержень довжиною 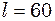 см здійснюють синхронно малі коливання навколо горизонтальної осі. Знайти відстань від центра стержня до цієї осі.
см здійснюють синхронно малі коливання навколо горизонтальної осі. Знайти відстань від центра стержня до цієї осі.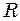 здійснює малі коливання навколо точки
здійснює малі коливання навколо точки 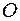 , рис. 9.12. Знайти їх період, якщо коливання відбуваються:
, рис. 9.12. Знайти їх період, якщо коливання відбуваються: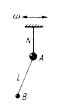
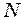 - нитка, до нижнього кінця якої підвішена кулька
- нитка, до нижнього кінця якої підвішена кулька 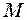 і
і 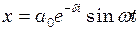 . Знайти:
. Знайти: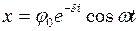 . Знайти:
. Знайти: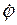 і кутове прискорення
і кутове прискорення 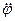 тіла в момент часу
тіла в момент часу 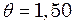 . Яким буде значення
. Яким буде значення 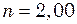 рази? У скільки разів слід збільшити опір середовища, щоб коливання стали неможливі?
рази? У скільки разів слід збільшити опір середовища, щоб коливання стали неможливі?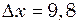 см. З яким періодом буде коливатися вантаж у вертикальному напрямі? Логарифмічний декремент згасання
см. З яким періодом буде коливатися вантаж у вертикальному напрямі? Логарифмічний декремент згасання 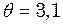 .
.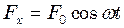 , що співпадає за напрямом з віссю
, що співпадає за напрямом з віссю 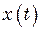 .
.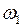 і
і 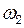 амплітуда швидкості частинки дорівнює половині максимального значення. Знайти:
амплітуда швидкості частинки дорівнює половині максимального значення. Знайти: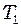 до
до 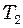 ? Швидкість звуку в по
? Швидкість звуку в по 


