
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади розв’язування задач.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приклад 9.1. Матеріальна точка здійснює гармонічні коливання з частотою Розв’язок: За означенням середньої швидкості маємо:
де
За формулою (2), поклавши
Згідно означення середнього прискорення, запишемо
де
За формулою (3), прийнявши
Підставивши у формули (2), (3), (5) і (6) числові значення величин, одержимо:
Зауваження: Перевіркою легко переконатися в тому, що середні величини
Приклад 9.2. За яку частину періоду точка, що здійснює гармонічні коливання, пройде шлях, рівний: 1) половині амплітуди, якщо в початковий момент вона знаходилася в положенні рівноваги; 2) одній третини амплітуди, якщо в початковий момент вона знаходилася в крайньому положенні?
Розв’язок: 1. Шлях
Щоб знайти початкову фазу
Підставивши в (2) значення
2)Точка рухається з крайнього положення, тому початкові умови будуть такі:
Щоб уникнути помилки, врахуємо, що вихідне рівняння (1) виражає зміщення точки при гармонічному коливанні, відрахованому від положення рівноваги, але не шлях, пройдений точкою; тільки в частковому вигляді руху точки з положення рівноваги до крайнього положення ці величини чисельно рівні (цим ми скористалися в першому випадку). Якщо точка, рухаючись з крайнього положення, пройшла шлях
Приклад 9.3. Матеріальна точка бере участь в трьох коливаннях, що здійснюються вздовж однієї прямої і задаються рівняннями:
Зміщенні задані в сантиметрах. Визначити амплітуду і початкову фазу результуючого коливання. Записати його рівняння. Розв’язок: Точка бере участь в трьох гармонічних коливаннях, оскільки зміщення
Порівнявши (1), (2), (3а) із загальним рівнянням зміщення гармонічних коливань, бачимо, що коливання, які додаються, характеризуються наступними величинами: амплітуди За допомогою формул (13) і (14) можна спочатку додати будь-які два з трьох заданих коливань. Потім, ще раз застосувавши ці формули, знайти амплітуду
До цього ж результату прийдемо швидше, застосувавши метод векторних діаграм. Суть його полягає в тому, що амплітуду На рисунку побудована векторна діаграма згідно даних умови задачі. З графіка зразу отримуємо:
Приклад 9.4. Відомо, що складне коливання, графік якого наведено на рисунку, складається з двох синусоїдальних коливань. Знайти їх частоти і амплітуди.
Розв’язок: Наведений графік зображає гармонічне коливання амплітуда якого повільно періодично змінюється. Таке коливання, що називається биттям, одержуються в результаті додавання двох однаково напрямлених гармонічних коливань з частотами, що мало відрізняються. При цьому частота складних коливань
А частота зміни амплітуди, яка називається частотою биття, дорівнює різниці частот:
З графіка видно, що за одну секунду відбулося дев’ять повних коливань, отже
Амплітуда складного коливання в кожний момент визначається за формулою (13). При цьому її максимальне значення при
Мінімальне значення амплітуди одержимо при
Але з графіка видно, що
Приклад 9.5. Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, виражених рівняннями
Розв’язок: Оскільки циклічні частоти коливань, що додаються, однакові, траєкторією точки буде еліпс. Виключивши час
Це канонічне рівняння еліпса з півосями Швидкість точки
Аналогічно знайдемо шукане прискорення:
За формулами (2) і (3) маємо:
Підставивши ці значення в формули (1) і (2), знайдемо:
Взявши Зауваження. Було б помилкою шукати прискорення
Приклад 9.6. Куля радіусом Розв’язок: Куля, що висить на нитці, являє собою фізичний маятник. Його період
Таким чином, вважаючи маятник математичним, ми замінюємо кулю матеріальною точкою, розташованою в її центрі, що викликає деяку похибку в обчисленні періоду. Знайдемо відношення періодів
Момент інерції кулі відносно осі коливань рівний
Підставивши це значення в (2), одержимо:
Звідси знайдемо відносну похибку в обчисленні періоду:
Приклад 9.7. Тіло, що нерухомо висить на циліндричній пружині, розтягує її на Розв’язок: Якщо б тіло здійснювало коливання тільки під дією сили пружності пружини 1) тіло нерухомо висить на пружині. Рівнодійна сил, прикладених до тіла,
2) тіло зміщене з положення рівноваги на Будемо вважати
Розкриваючи дужки і враховуючи (1), одержимо:
З (2) видно, що рівнодійна сил
Приклад 9.8. Ареометр масою 55 г, що плаває в розчині сірчаної кислоти, показує, що густина рідини Розв’язок: На занурений в рідину ареометр діють дві сили: сила тяжіння 1) ареометр знаходиться в рівновазі. Прикладені до нього сили врівноважуються. Прийнявши напрям вниз за додатній, запишемо:
2) ареометр зміщений з положення рівноваги по вертикалі на величину Оскільки зміниться об’єм зануреної частини приладу, виштовхувальна сила також зміниться. До ареометра буде прикладена рівнодійна, напрямлена по вертикалі вгору і рівна
де
де
Приклад 9.9. Енергія згасаючих коливань маятника, що відбуваються в деякому середовищі, за час Розв’язок: Коефіцієнт опору
Щоб знайти величину
виражає амплітуду коливань, що зменшується з часом. Енергія коливань пропорційна квадрату амплітуди. Отже, позначивши початкову і кінцеву енергію коливань через
Тепер з (2) і (3) маємо
Підставивши знайдене значення
Підставляючи числові значення в останнє рівняння, одержимо:
Приклад 9.10. Гиря масою 0,500 кг підвішена до пружини, жорсткість якої 1) за час, протягом якого відбулося 2) за час двох коливань ( Розв’язок: Опір середовища зменшує частоту вільних коливань. Циклічна частота згасаючих коливань визначається за формулою
звідки період рівний
Власну циклічну частоту
Коефіцієнт згасання
Щоб знайти величину
Користуючись введеними позначеннями, можна записати:
Підставивши числові значення Тепер перепишемо формулу (1) з урахуванням (3):
Одержали квадратне рівняння відносно періоду
Приступаючи до обчислень, зауважимо, що в першому випадку
У другому випадку неможна відкидати величину
Приклад 9.11. Чому дорівнює амплітуда вимушених коливань при резонансі Розв’язок: Амплітуда вимушених коливань залежить від частоти
де З формули (9.22) можна також вивести просте співвідношення між величинами 1) 2)
Підставивши це значення
Виразимо власну частоту
Тут
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 819; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.116.245 (0.015 с.) |

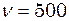 Гц і амплітудою
Гц і амплітудою  см. Визначити середні значення швидкості
см. Визначити середні значення швидкості  і прискорення
і прискорення  точки на шляху від її крайнього положення до положення рівноваги, а також знайти максимальні значення цих величин:
точки на шляху від її крайнього положення до положення рівноваги, а також знайти максимальні значення цих величин: 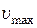 і
і  .
. (1)
(1) - шлях, пройдений за час
- шлях, пройдений за час  . В даному випадку
. В даному випадку  ;
;  , оскільки за період
, оскільки за період 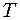 точка, що здійснює коливання, проходить шлях рівний чотирьом амплітудам. Підставивши ці значення
точка, що здійснює коливання, проходить шлях рівний чотирьом амплітудам. Підставивши ці значення  , одержимо:
, одержимо: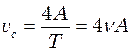 .
. , знайдемо максимальну швидкість:
, знайдемо максимальну швидкість: . (3)
. (3) (4)
(4) . В даному випадку початкова швидкість
. В даному випадку початкова швидкість 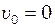 , кінцева швидкість
, кінцева швидкість  . Підставимо значення
. Підставимо значення 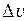 і
і 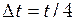 у формулу (4), використовуючи співвідношення
у формулу (4), використовуючи співвідношення 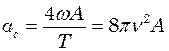 . (5)
. (5)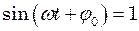 , знайдемо максимальне прискорення:
, знайдемо максимальне прискорення: . (6)
. (6) см/с,
см/с,  см/с2,
см/с2,  см/с,
см/с,  см/с2.
см/с2.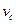 і
і 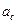 на шляху від крайнього положення до положення рівноваги точки, що коливається, не дорівнюють середньому арифметичному між початковим і кінцевим значеннями цих величин. Методом середнього арифметичного для знаходження
на шляху від крайнього положення до положення рівноваги точки, що коливається, не дорівнюють середньому арифметичному між початковим і кінцевим значеннями цих величин. Методом середнього арифметичного для знаходження 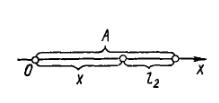
 , пройдений точкою, що здійснює гармонічне коливання, при русі від положення рівноваги до крайнього положення, дорівнює зміщенню
, пройдений точкою, що здійснює гармонічне коливання, при русі від положення рівноваги до крайнього положення, дорівнює зміщенню  , що визначається з рівняння (1), яке запишемо у вигляді:
, що визначається з рівняння (1), яке запишемо у вигляді: (1)
(1)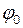 , скористаємося початковими умовами задачі:
, скористаємося початковими умовами задачі: 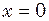 при
при 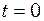 . Підставивши ці значення
. Підставивши ці значення  і
і 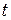 в (1), одержимо
в (1), одержимо 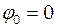 , отже
, отже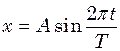 (2)
(2) , одержимо шуканий час, виражений в долях періоду:
, одержимо шуканий час, виражений в долях періоду: .
. при
при 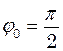 . Отже
. Отже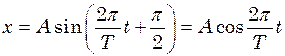 (3)
(3) , то, як видно з рисунка, її зміщення дорівнює
, то, як видно з рисунка, її зміщення дорівнює  . Підставивши це значення в формулу (3), одержимо
. Підставивши це значення в формулу (3), одержимо 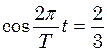 . Звідси, користуючись таблицею косинусів, знайдемо шуканий час в долях періоду:
. Звідси, користуючись таблицею косинусів, знайдемо шуканий час в долях періоду: ,
,  .
. (1)
(1) (2)
(2)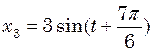 (3)
(3)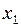 ,
, 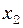 ,
, 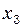 , є синусоїдальними (косинусоїдальними) функціями часу. Результуюче коливання точки також буде гармонічним. Його амплітуду і фазу можна знайти за формулами (13) і (14). Однак вони виведені для випадку, коли рівняння коливань, що додаються, містять одну і ту ж тригонометричну функцію: синус або косинус. Тому перепишемо рівняння (3), виразивши
, є синусоїдальними (косинусоїдальними) функціями часу. Результуюче коливання точки також буде гармонічним. Його амплітуду і фазу можна знайти за формулами (13) і (14). Однак вони виведені для випадку, коли рівняння коливань, що додаються, містять одну і ту ж тригонометричну функцію: синус або косинус. Тому перепишемо рівняння (3), виразивши 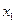 через косинус:
через косинус: (3а)
(3а) см, циклічні частоти
см, циклічні частоти  рад/с, початкові фази
рад/с, початкові фази  ,
,  ,
,  .
. і початкову фазу
і початкову фазу 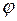 результуючого коливання.
результуючого коливання.
 ,
,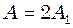 , тобто
, тобто 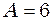 см. Тепер запишемо рівняння результуючого коливання:
см. Тепер запишемо рівняння результуючого коливання:  .
.
 виявляється рівною пів сумі частот коливань
виявляється рівною пів сумі частот коливань  і
і  , що додаються:
, що додаються: (1)
(1) (2)
(2) Гц. За цей час відбулося два повних цикли зміни амплітуди, отже
Гц. За цей час відбулося два повних цикли зміни амплітуди, отже 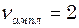 Гц. Підставивши в (1) і (2) значення
Гц. Підставивши в (1) і (2) значення  ,
, 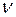 і розв’язавши цю систему рівнянь, знайдемо:
і розв’язавши цю систему рівнянь, знайдемо: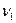 =8 Гц,
=8 Гц, 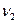 =10 Гц.
=10 Гц.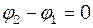 рівне:
рівне: (3)
(3) :
: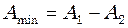 (4)
(4)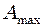 =2 см,
=2 см,  =0. Підставивши ці значення
=0. Підставивши ці значення  см.
см. ;
;  (зміщення задані в сантиметрах). Знайти рівняння траєкторії точки і побудувати її на графіку. Показати напрям руху точки. Визначити швидкість і прискорення точки в момент часу
(зміщення задані в сантиметрах). Знайти рівняння траєкторії точки і побудувати її на графіку. Показати напрям руху точки. Визначити швидкість і прискорення точки в момент часу  с.
с.

 см і
см і  см. Щоб визначити напрям руху точки, врахуємо, що в момент
см. Щоб визначити напрям руху точки, врахуємо, що в момент  см і, отже, точка знаходиться в положенні
см і, отже, точка знаходиться в положенні  при її русі по еліпсу дорівнює векторній сумі швидкостей
при її русі по еліпсу дорівнює векторній сумі швидкостей 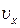 і
і 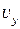 коливань, що додаються. Оскільки ці коливання взаємно перпендикулярні, то
коливань, що додаються. Оскільки ці коливання взаємно перпендикулярні, то (1)
(1)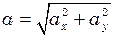 (2)
(2)

 см/с,
см/с,  см/с2.
см/с2.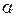 як похідну
як похідну  . Величина
. Величина 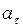 точки, що рухається, але не повне прискорення
точки, що рухається, але не повне прискорення 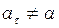 .
. см, підвішена на нитці довжиною
см, підвішена на нитці довжиною  см. Визначити відносну похибку, яку допускають, коли обчислюють період коливань маятника, вважаючи його математичним маятником довжиною
см. Визначити відносну похибку, яку допускають, коли обчислюють період коливань маятника, вважаючи його математичним маятником довжиною  см.
см. виражається формулою (12). Якщо прийняти маятник за математичний, то його період
виражається формулою (12). Якщо прийняти маятник за математичний, то його період  потрібно знаходити за формулою (10), вважаючи згідно умови довжину
потрібно знаходити за формулою (10), вважаючи згідно умови довжину 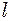 рівною відстані від точки підвісу до центра ваги кулі:
рівною відстані від точки підвісу до центра ваги кулі: (1)
(1) (2)
(2)
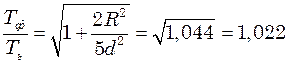 .
. або 2,2%.
або 2,2%.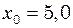 см. Потім тіло було зміщене з положення рівноваги по вертикалі і відпущене, в результаті чого воно стало здійснювати коливання. Знайти їх період.
см. Потім тіло було зміщене з положення рівноваги по вертикалі і відпущене, в результаті чого воно стало здійснювати коливання. Знайти їх період. , їх період можна було б визначити за формулою (11). В даному випадку на тіло ще діє сила тяжіння
, їх період можна було б визначити за формулою (11). В даному випадку на тіло ще діє сила тяжіння  . Щоб з’ясувати її вплив на коливання вантажу, розглянемо сили, що діють на тіло, в двох положеннях:
. Щоб з’ясувати її вплив на коливання вантажу, розглянемо сили, що діють на тіло, в двох положеннях: . Прийнявши напрям вниз за додатній, запишемо
. Прийнявши напрям вниз за додатній, запишемо (1)
(1) .
.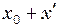 . Рівнодійна сил, прикладених до тіла, рівна:
. Рівнодійна сил, прикладених до тіла, рівна: .
. . (2)
. (2)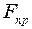 і
і 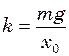 , знайдемо період цих коливань:
, знайдемо період цих коливань: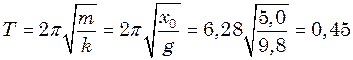 с.
с. г/см3. Якщо прилад змістити трохи з положення рівноваги по вертикалі і відпустити, він почне коливатися. Вважаючи коливання незгасаючими, визначити їх період, якщо радіус циліндричної трубки ареометра, в якому знаходиться його шкала, дорівнює
г/см3. Якщо прилад змістити трохи з положення рівноваги по вертикалі і відпустити, він почне коливатися. Вважаючи коливання незгасаючими, визначити їх період, якщо радіус циліндричної трубки ареометра, в якому знаходиться його шкала, дорівнює  см.
см. , що рівна вазі витісненої тілом рідини:
, що рівна вазі витісненої тілом рідини:  , де
, де  - об’єм витісненої рідини, рівний об’єму зануреної частини ареометра. Як і в попередній задачі, з’ясуємо співвідношення між діючими силами в двох випадках:
- об’єм витісненої рідини, рівний об’єму зануреної частини ареометра. Як і в попередній задачі, з’ясуємо співвідношення між діючими силами в двох випадках: (1)
(1)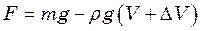 (2)
(2) - зміна об’єму зануреної частини приладу. Підставимо це значення
- зміна об’єму зануреної частини приладу. Підставимо це значення  у (2) і розкривши дужки, одержимо з врахуванням (1)
у (2) і розкривши дужки, одержимо з врахуванням (1) (3)
(3) - стала величина. Бачимо, що на ареометр діє сила, пропорційна зміщенню, взятому з протилежним знаком, тобто квазіупружна сила. Отже він здійснює гармонічні коливання, період яких дорівнює:
- стала величина. Бачимо, що на ареометр діє сила, пропорційна зміщенню, взятому з протилежним знаком, тобто квазіупружна сила. Отже він здійснює гармонічні коливання, період яких дорівнює: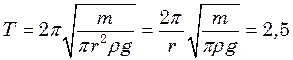 с.
с. хв. зменшилася в
хв. зменшилася в  разів. Визначити коефіцієнт опору, якщо маса маятника
разів. Визначити коефіцієнт опору, якщо маса маятника 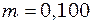 кг.
кг. пов'язаний з коефіцієнтом згасання
пов'язаний з коефіцієнтом згасання 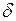 і масою
і масою 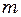 тіла співвідношенням
тіла співвідношенням (1)
(1) (2)
(2) і
і 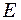 , можна записати:
, можна записати: ;
;  (3)
(3) . Логарифмуючи, знаходимо:
. Логарифмуючи, знаходимо:
 ,
,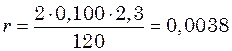 кг/с.
кг/с.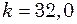 Н/м, і здійснює згасаючі коливання. Визначити їх період у двох випадках:
Н/м, і здійснює згасаючі коливання. Визначити їх період у двох випадках: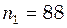 коливань, амплітуда зменшилася в
коливань, амплітуда зменшилася в 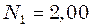 рази;
рази; ) амплітуда зменшилась в
) амплітуда зменшилась в  разів.
разів. ,
, (1)
(1)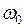 виразимо через формулу періоду пружинного маятника, знаючи масу
виразимо через формулу періоду пружинного маятника, знаючи масу 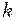 пружини:
пружини: рад/с. (2)
рад/с. (2) (3)
(3)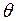 скористаємося рівнянням згасаючих коливань. Амплітуду, що зменшується з часом, виразимо наступним чином:
скористаємося рівнянням згасаючих коливань. Амплітуду, що зменшується з часом, виразимо наступним чином: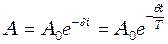 . (4)
. (4) , тоді з (4) випливає
, тоді з (4) випливає 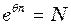 , звідки, логарифмуючи, маємо:
, звідки, логарифмуючи, маємо: .
.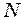 і
і  для двох випадків, виконаємо обчислення:
для двох випадків, виконаємо обчислення:  .
. .
. (5)
(5) . Тому, зберігаючи достатньо високу точність обчислень, можна в формулі (5) знехтувати членом
. Тому, зберігаючи достатньо високу точність обчислень, можна в формулі (5) знехтувати членом 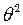 і тоді:
і тоді: с.
с. с.
с.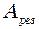 , якщо при дуже малій (порівняно з власною) частоті вимушених коливань вона рівна
, якщо при дуже малій (порівняно з власною) частоті вимушених коливань вона рівна 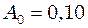 см, а логарифмічний декремент згасання
см, а логарифмічний декремент згасання  ?
?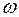 вимушуючої сили (9.22). При деякому значенні
вимушуючої сили (9.22). При деякому значенні 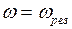 , що визначається умовою
, що визначається умовою  , настає явище резонансу: амплітуда досягає максимального значення
, настає явище резонансу: амплітуда досягає максимального значення  ,
,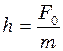 .
. і
і  . Враховуючи співвідношення, що випливають з умови задачі:
. Враховуючи співвідношення, що випливають з умови задачі: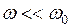 ;
;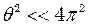 , звідки випливає, що
, звідки випливає, що  , відкинемо члени
, відкинемо члени  і
і  у (22):
у (22):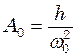
 у порівнянні з
у порівнянні з  , одержимо:
, одержимо: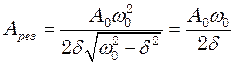 (2)
(2) ;
;  - період вільних коливань при відсутності опору;
- період вільних коливань при відсутності опору;  , знайдемо остаточну відповідь:
, знайдемо остаточну відповідь: см.
см.


