
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диагностические модели объектовСодержание книги
Поиск на нашем сайте
В общем случае под диагностической моделью системы объекта понимают формальное ее описание или графоаналитическое представление, отражающее основные изменения, происходящие в объекте диагностирования при эксплуатации. В качестве диагностических моделей сложных технических систем могут рассматриваться дифференциальные уравнения, логические соотношения, диаграммы прохождения сигналов, графы причинно-следственных связей и др. Аналитические модели Аналитические модели нашли широкое применение при исследовании отдельных агрегатов объектов и их элементов. В общем случае связь между выходными параметрами гидравлического агрегата, находящегося в исправном состоянии, его структурными (внутренними) параметрами и внешними воздействиями в определенный момент времени может быть представлена в виде векторной функции
где Выражение (1.21) представляет собой систему передаточных функций исправного объекта. Аналогично система передаточных функций для объекта, находящегося в q-м неисправном состоянии, будет
При этом вектор начальных значений внутренних переменных В дальнейшем для фактических значений векторов
Передаточные функции объектов вида (1.21) или (1.22) обычно получают путем анализа системы нелинейных дифференциальных уравнений, описывающих их работу. Если для конкретного случая эту систему путем различных методов линеаризации для эксплуатационного диапазона изменения параметров векторов
где Применение в качестве диагностических моделей линейных операторов позволяет сформулировать условия работоспособности объекта в общем виде как ограничения для перемещений полюсов и нулей передаточной функции на плоскости комплексных переменных и определить допустимые изменения контролируемых параметров. Однако для построения такой модели необходимо измерять с достаточной точностью большое число параметров объекта, что практически нереализуемо. В связи с этим на практике обычно ограничиваются построением модели на основе передаточных функций для ограниченного числа входов и выходов.
|
||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

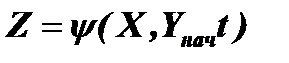 (1.21)
(1.21) - вектор выходных параметров агрегата;
- вектор выходных параметров агрегата; 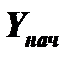 - вектор начальных значений структурных параметров агрегата;
- вектор начальных значений структурных параметров агрегата; 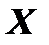 - вектор управляющих воздействий;
- вектор управляющих воздействий;  - время.
- время. (1.22)
(1.22)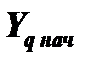 в общем случае не совпадает с вектором
в общем случае не совпадает с вектором  ,
, 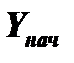 и
и 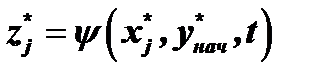
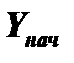 удается свести к эквивалентному линеаризованному виду, то в результате аналитических преобразований диагностическая модель объекта приобретает вид
удается свести к эквивалентному линеаризованному виду, то в результате аналитических преобразований диагностическая модель объекта приобретает вид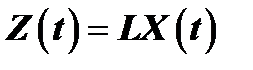 (1.23)
(1.23)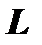 - линейный оператор.
- линейный оператор.


