Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятностная модель изменения потока (интенсивности) отказов во времениСодержание книги
Поиск на нашем сайте
Эта модель получена с помощью нового логарифмически равномерного (логравномерного) закона распределения, который характеризуется двумя параметрами с и d. Так же как и у известного равномерного распределения, параметр с – это нижняя граница распределения, при которой вероятность безотказной работы P(c}= 1. Параметр d - это верхняя граница распределения, когда P(d}= 0. Функции нового распределения имеют следующий вид. Функция вероятности безотказной работы
Функция плотности вероятности
Функция интенсивность отказов
Формула для определения гамма- процентного ресурса R( γ ) (при допустимой вероятности безотказной работы γ). следует из формулы (1) и имеет вид
Анализ этого распределения выявил ряд особых свойств. Например, из формулы ((2.10)) следует, что у этого распределения медиана t 50= dc , в то время как у равномерного распределения t 50=0,5(с + d). Математическое моделирование выявило неожиданное поведение функции интенсивности отказов ((2.9) при различных соотношениях параметров c и d (см. Рис. 2.14). График интенсивности отказов при очень больших отношениях d/c (например, 45 и более) напоминает хорошо известную из теории надежности характеристику интенсивности (или потока) отказов в течении жизненного цикла объекта исследования. С этой точки зрения жизненный цикл условно разбивается на три этапа: • начальный и относительно небольшой этап «выжигания» дефектов изготовления или освоения производства продукции, когда наблюдается уменьшение потока отказов, • основной этап с минимальным и стабильным уровнем интенсивности отказов, • заключительный этап эксплуатации, когда сказываются факторы старения (изнашивания) продукции, что приводит к резкому возрастанию интенсивности отказов.
Рис. 2.14 – Интенсивность отказов при разных величинах d (10, 30, 50 и 100). Примечание - кружками обозначены точки экстремума (минимума) кривых На Рис. 2.14 приведены графики интенсивности отказов при с = 1 и нескольких значениях d, на которых хорошо видны указанные этапы жизненного цикла особенно при больших значениях d. Советуем обратить внимание на кривую для d = 100. Если считать, что эта величина характеризует максимально-возможный срок жизни человека заданной популяции, то эта кривая удивительным образом соответствует демографическим закономерностям убыли населения различных возрастных групп. На графике виден первый участок снижения интенсивности убыли населения детского возраста к 7-10 годам жизни.
После этого интенсивность убыли стабилизируется примерно до 70 -75 - летнего возраста, достигая минимума к 37-38 годам. После 80 лет жизни наблюдается резкий рост интенсивности убыли населения старшего возраста. Возможно, что сходство вида этого графика с демографическими характеристиками не случайно и поэтому целесообразно продолжить изучение возможностей логравномерного распределения для прогнозирования надежности машин.
2.2.5 Эмперические кривые состояния объектов контроля (машин и механизмов)
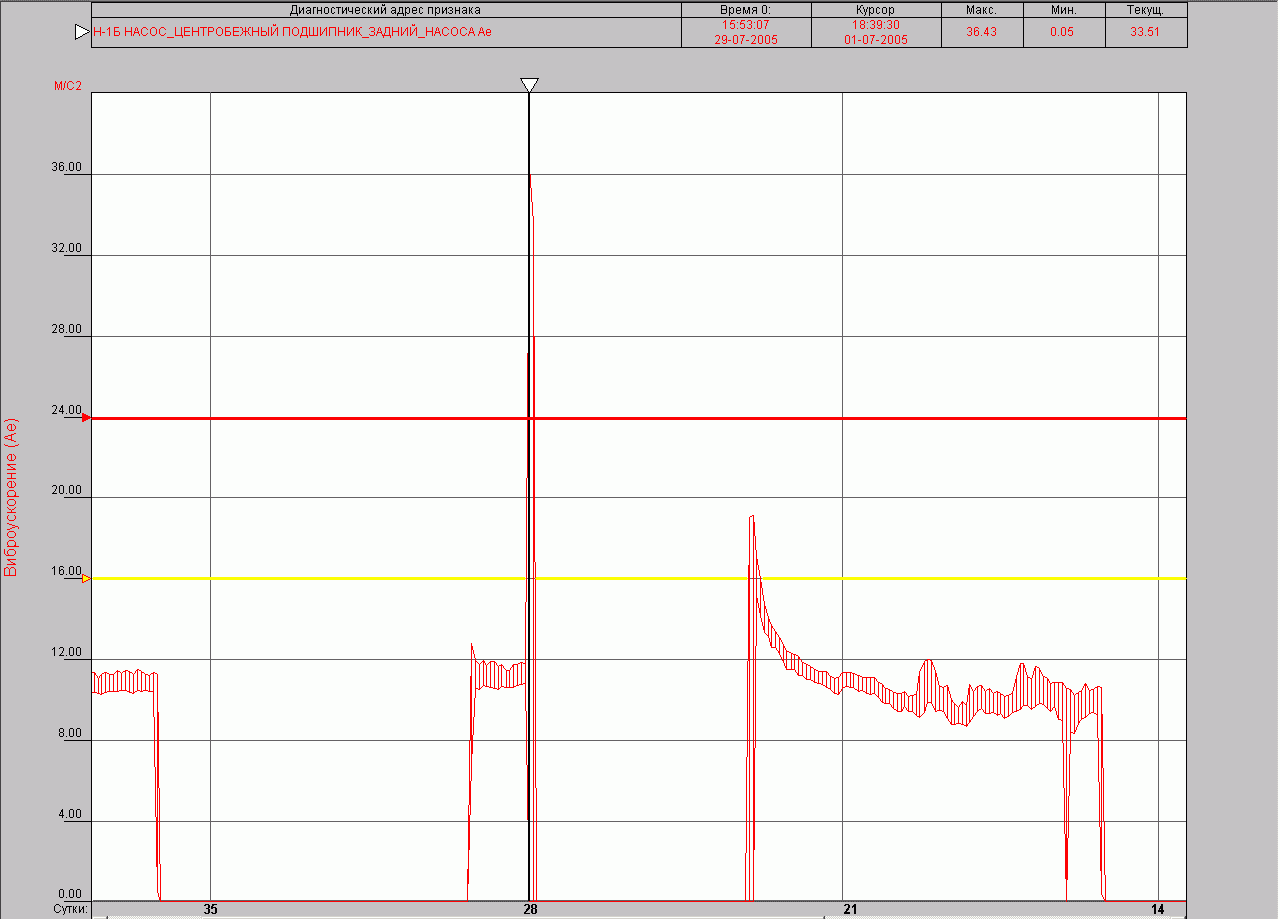
Рис. 2.15 – Тренд вибропараметра
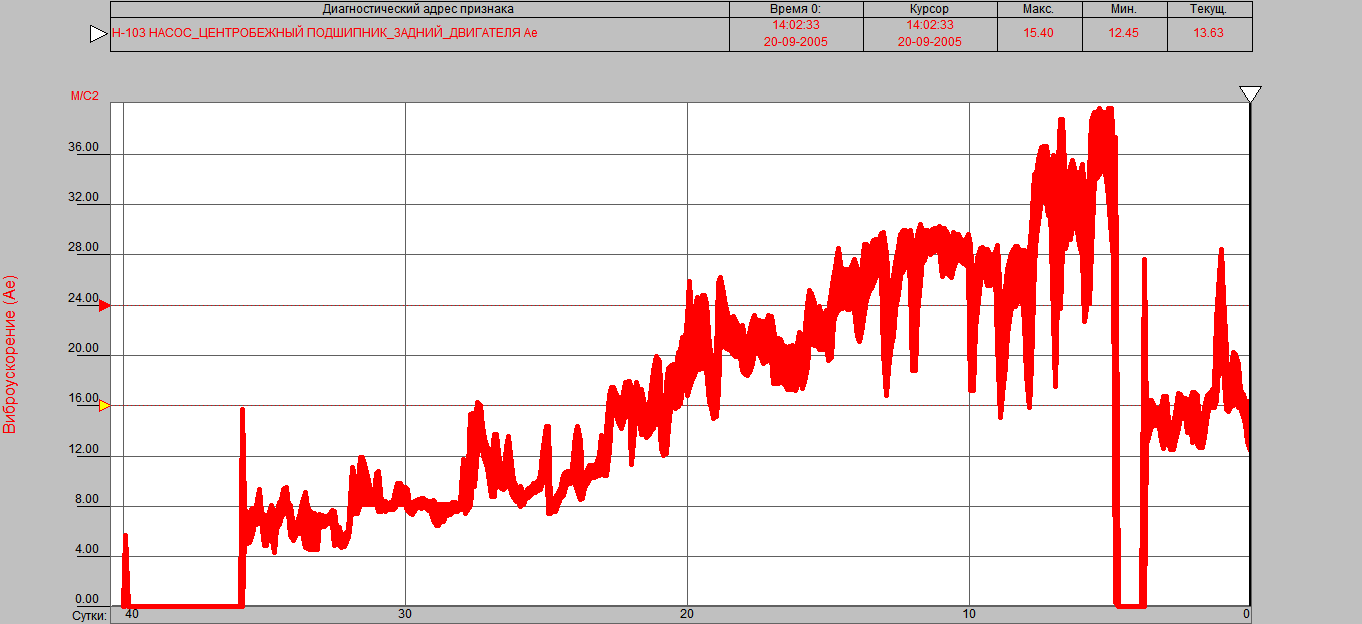
Рис. 2.16 – Тренд вибропараметра
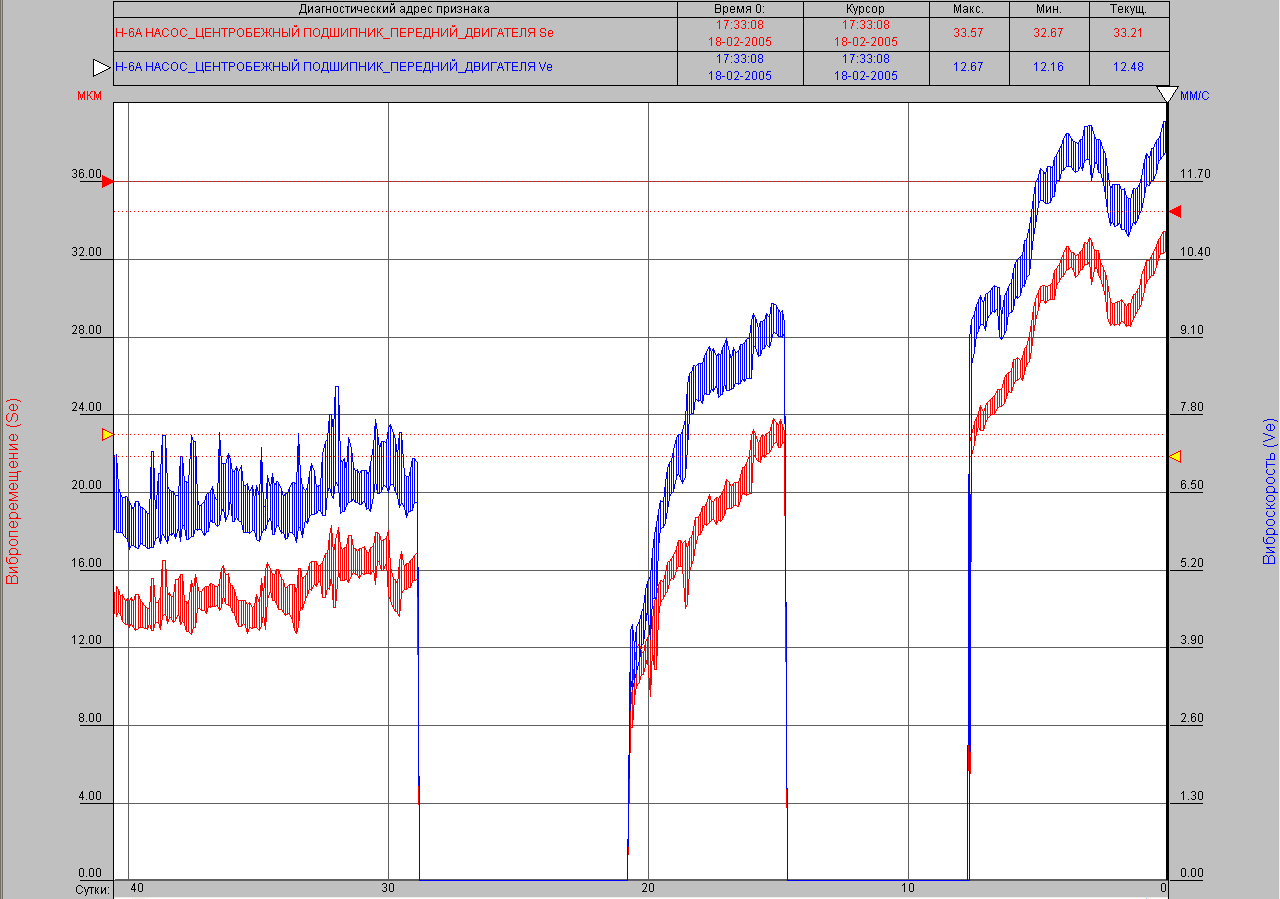
Рис. 2.17 – Тренд вибропараметра
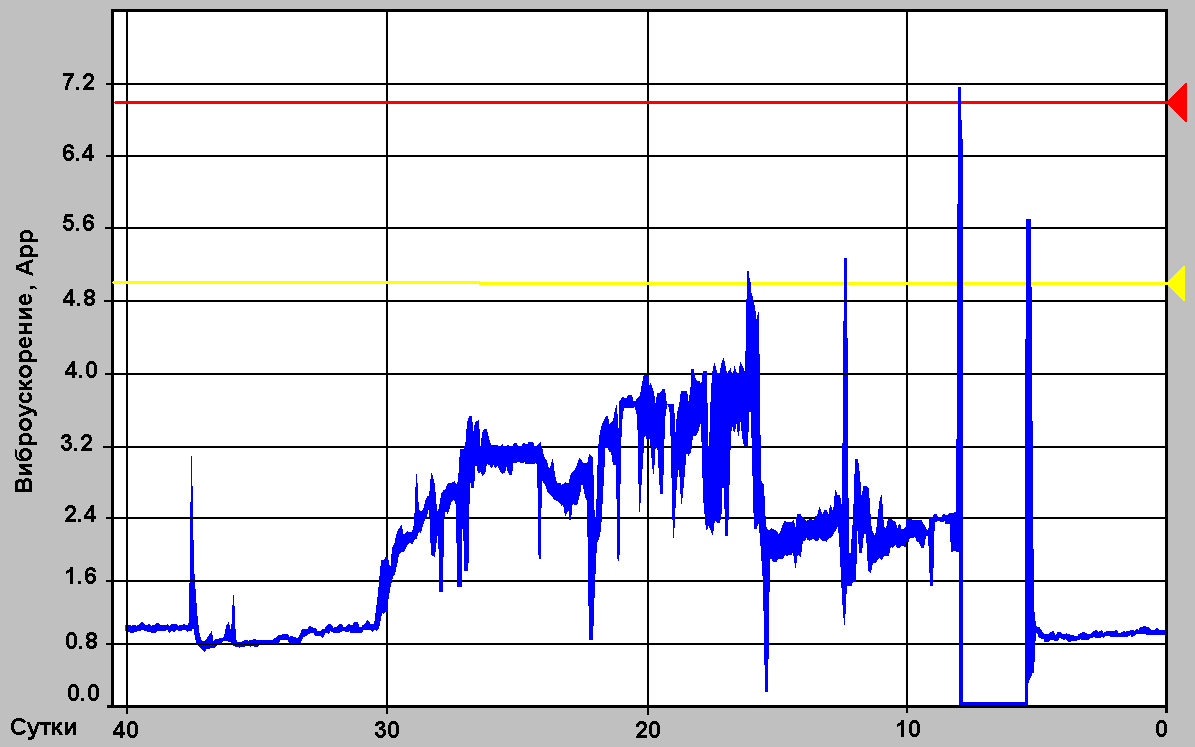
Рис. 2.18 – Тренд вибропараметра
|
|||||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.7.179 (0.01 с.) |

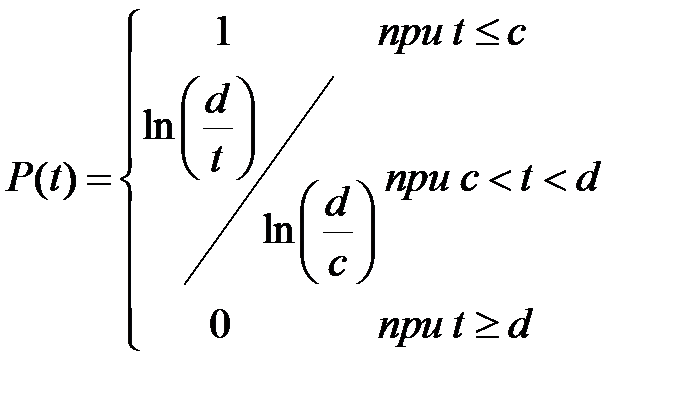 ,
,
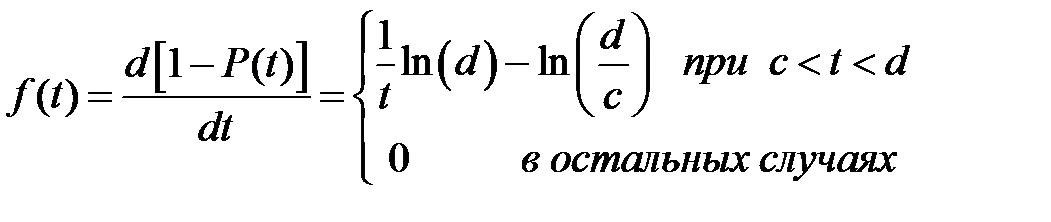 ,
,
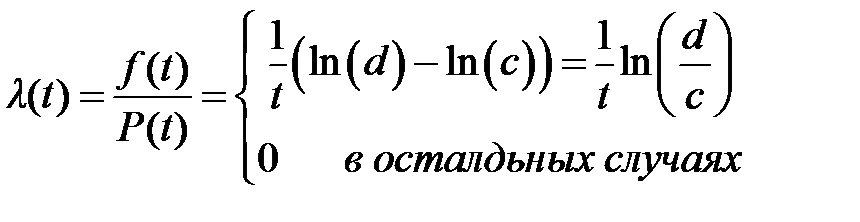 ,
,
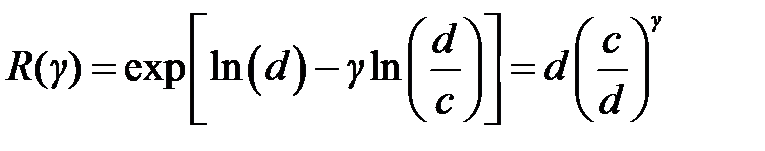 ,
,