
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика выполнения работы и ее обоснованиеСодержание книги
Поиск на нашем сайте
В соответствии с теорией Нернста растворение малорастворимых твердых тел протекает в диффузионной области, то есть лимитируется процессами диффузии. Если наблюдаемая скорость лимитируется процессами диффузии, то скорость такого процесса описывается уравнением диффузии.
Допустим, что кусок твёрдого тела с поверхностью S растворяется в насыщенном растворе этого вещества при перемешивании. Перемешивание жидкости не захватывает полностью всего его объема. При любой скорости перемешивания всегда имеется некоторый слой, прилегающий к поверхности твердого тела, который остаётся в некоторой степени неподвижным. Перенос вещества в этом случае осуществляется молекулярной диффузией. В этом, так называемом ламинарном слое концентрация растворенного вещества переменная и изменяется от насыщенной у самой поверхности твердого тела до некоторой величины на внешней границе ламинарного слоя. При этом, вследствие перемешивания, концентрация растворенного вещества на внешней границе ламинарного слоя равна концентрации вещества во всём объёма раствора. Толщина диффузионного слоя δ определяется природой твердого вещества, природой жидкости и зависит от температуры и скорости перемешивания: δ = А (ω)–0,5, (5.2) где А – постоянная величина; ω– скорость перемешивания. Градиент концентрации вещества в этом ламинарном слое:
Тогда, согласно закону Фика, в установившемся режиме диффузии количество вещества dm, поступившее за время dt в реактор через этот слой, можно выразить уравнением:
Массу вещества, содержащуюся в растворе, можно выразить как произведение концентрации c на объем раствора V, то есть m = Vc. Считая, что в процессе растворения объем раствора практически остается постоянным, можно записать: dm = Vdc (5.5) Тогда, подставив значение dm из уравнения (5.5) в уравнение (5.4), можно выразить изменение концентрации раствора во времени, т.е. скорость растворения:
или
Представив
Таким образом, константа скорости растворения k в уравнении будет определятся величинами D, S, δ, V. При постоянных D, S, δ, V величина k остается постоянной. Особенно хорошо это постоянство соблюдается в случае растворения мало или труднорастворимых веществ, так как концентрация раствора изменяется незначительно, то и коэффициент диффузии зависит практически только от температуры. Величина поверхности твердого тела S также остается постоянной, пока размеры твердого тела заметно не изменяются. Толщина диффузионного слоя d, как было отмечено, зависит от условий перемешивания при растворении и сохраняется при неизменной скорости перемешивания постоянной. Величина V может быть приравнена к объему раствора. Учитывая постоянство k, разделим переменные в уравнении (5.8) и получим:
Интегрируя уравнение (5.9), находим: –ln(c нас – c) = kt + const. (5.10) Время отсчитывают от момента погружения растворяемого тела в чистый растворитель. Тогда при t = 0, c = 0. Из этих граничных условий следует, что const = –ln c нас и, таким образом,
или
Если уравнение (5.11) записать следующим образом:
то видим, что экспериментальные даные должны укладываться на прямую в координатах: ln(c нас – c) = ƒ(t), tg α = – k = Принимаем, что для труднорастворимых солей электропроводность в первом приближении пропорциональна концентрации соли в растворе, то есть L = В × c, то подставив значение c = ƒ(L) в уравнение (5.12), можно записать:
где L нас – удельная электропроводность насыщенного раствора данной соли; L – удельная электропроводность раствора к моменту времени t. Представим уравнение (5.14) в виде
Полагая, y = – kt + в. (5.15) Видим, что уравнение (5.15) является уравнением прямой. Тогда, построив график в координатах
Порядок выполнения работы
1. Подключают модуль «Электрохимия» к центральному контроллеру с помощью соединительного кабеля. Подключают центральный контроллер к сети (напряжение 220 В, частота 50 Гц). Электроды электрохимической ячейки подключают к разъёмам I вх и I вых без учёта полярности. По заданию преподавателя настраивают скорость вращения мешалки. 2. В стакан ёмкостью 100 см3 наливают дистиллированную воду и измеряют её электропроводность в миллисименсах (мСм). 3. Вносят в стакан 1 г твёрдого вещества по заданию преподавателя, включают секундомер. 4. Первые 5 мин делают измерения электропроводности раствора каждые 30 с, затем через каждые 5 мин в течение 35 – 40 мин. Последующие измерения можно проводить через 10 – 20 мин. Измерения продолжают до тех пор, пока электропроводность не достигнет постоянной величины. 5. Измеряют электропроводность насыщенного раствора данного вещества L нас. 6. Строят графики L = ƒ(t), что эквивалентно c = ƒ(t) и 7. Изменяют скорость перемешивания и вновь повторяют опыт. 8. По результатам двух опытов формулируют заключение о влиянии скорости перемешивания на скорость растворения и об области протекания гетерогенного процесса.
Рекомендуемый вид таблицы
Растворяемое вещество – L нас. = мСм Скорость перемешивания =
Работа № 6 Изучение кинетики реакции
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.163.26 (0.007 с.) |

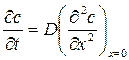 (5.1)
(5.1)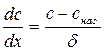 . (5.3)
. (5.3)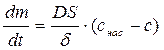 . (5.4)
. (5.4)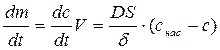 (5.6)
(5.6)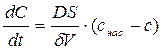 . (5.7)
. (5.7)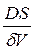 = k, можно записать
= k, можно записать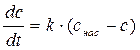 . (5.8)
. (5.8)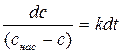 . (5.9)
. (5.9)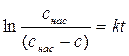 (5.11)
(5.11)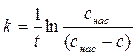 . (5.12)
. (5.12)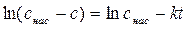 , (5.13)
, (5.13)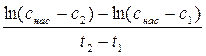 .
.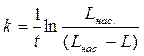 , (5.14)
, (5.14) 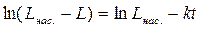 .
. 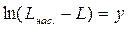 , а
, а 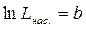 , получим:
, получим: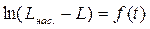 , найдём константу скорости растворения k как tg a этой прямой:
, найдём константу скорости растворения k как tg a этой прямой: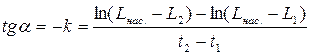 . (5.16)
. (5.16)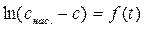 . Используя экспериментальные точки, более удовлетворительно лежащие на прямой графика, рассчитывают константу растворения k по уравнению (5.16).
. Используя экспериментальные точки, более удовлетворительно лежащие на прямой графика, рассчитывают константу растворения k по уравнению (5.16).


