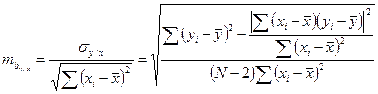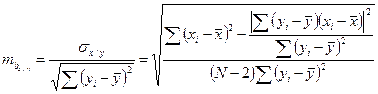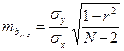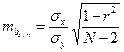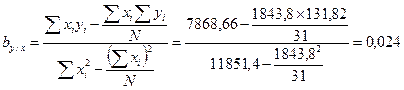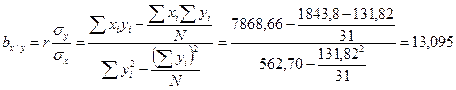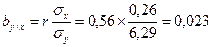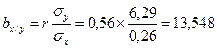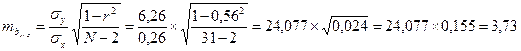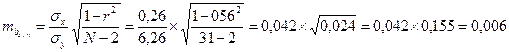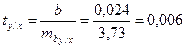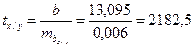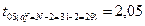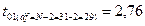Достоверность линий регрессии и коэффициентов регрессии

Для оценки достоверности, необходимо вычислить ошибки коэффициентов регрессии (m_{by / x} и m_{bx / y}) и критическое значение коэффициента «t».

Стандартное значение критерия Стьюдента (t ₀₅ или t ₀₁) определяется при df = N - 2. Если t > t ₀₅  нулевая гипотеза о недостоверности регрессии отклоняется, то есть, регрессия достоверна. Если t < t ₀₅  нулевая гипотеза о недостоверности регрессии принимается, то есть, регрессия недостоверна.

Пример 8. На основе данных о варьировании 31 сеянца алычи по сочетанию признаков «средняя длина листовой пластинки» («х», мм) и «диаметр штамба» («у», см) вычислить значения b_{y / x}b_{x / y} и оценить их достоверность.

Длина листовой пластинки «х», мм и диаметр штамба «у», см у 31 сеянца алычи

х	76,6	72,2	67,0	66,5	63,3	65,4	63,9	63,1	63,0	62,5	62,2
у	4,56	4,79	4,49	4,32	4,59	4,32	4,67	4,29	4,57	4,20	4,12
х	61,0	60,2	60,0	59,6	59,5	58,9	58,0	57,8	57,6	57,0
у	4,13	4,70	3,80	4,23	3,76	4,08	4,61	4,37	4,30	4,00
х	56,8	55,4	55,0	53,8	53,7	52,0	51,4	51,0	50,9	48,5
у	3,82	4,12	4,19	4,16	4,09	4,12	4,02	4,31	4,06	4,03

Решение:

1. Вычислим коэффициенты регрессии напрямую из исходных данных. Определим компоненты формул:

Σ x_i =1843,80

Σ y_i =131.82

Σ x_i ²=11851,40

Σ y_i ²=562,70

Σ x_iy_i = 7868,66

N = 31

Подставим эти компоненты в формулы:

Сравним вычисленные коэффициенты регрессии с теми, которые были получены при составлении уравнений регрессии:

1) при составлении уравнений на основе корреляционной решетки: b_{y / x} =0,022, b_{х / у} = 11,57;

2) при составлении уравнений на основе исходных данных: b_{y / x} =0,024, b_{х / у} = 13,09;

3) при вычислении коэффициентов регрессии напрямую из исходных данных: b_{y / x} =0,024, b_{х / у} = 13,095;

Сравнение показывает, что при составлении уравнений линейной регрессии на основе исходных данных величины коэффициентов регрессии почти точно совпадают со значениями коэффициентов регрессии, вычисленных по формулам.

2. Вычислим коэффициенты регрессии на основе значения коэффициента корреляции и средних квадратических отклонений:

r =0,56

σ_x =6,29

σ_y =0,26

Незначительные различия в значениях коэффициентов корреляции, вычисленных разными способами, объясняются округлениями в процессе вычисления r, σ_x и σ_y.

3. Оценим достоверность коэффициентов регрессии. Для этого необходимо вычислить ошибки репрезентативности каждого коэффициента регрессии: m_{by / x} и m_{bx / y}. Удобней использовать следующие формулы:

Так как t_{y / x} =0,006< t ₀₅ =2,05, нулевая гипотеза принимается, то есть, регрессия у / х недостоверна. Так как t _х/у =2182,5> t ₀₁ =2,76, нулевая гипотеза отклоняется, то есть, регрессия х / у достоверна.

Вывод: у сеянцев абрикоса – 1) диаметр штамба у сеянцев абрикоса не зависит от длины листовой пластинки; 2) длина листовой пластинки зависит от диаметра штамба.