Начальная школа выпуск 5 2006 год страница 88

Александрова Софья НОЛк-219

Статьи

Статья

Начальная школа выпуск 5 2006 год страница 88

https://n-shkola.ru/storage/archive/1407237212-1332344965.pdf

М.В. Амелина. Математическое лото

В одном из номеров журнала «Начальная школа» я познакомилась с разработкой к урокам русского языка, которая называется «Грамматическое домино». Эта идея меня увлекла, и по тому же принципу я составила «Математическое лото». Перед уроком я раздаю ученикам кар" точки с ответами. В ходе урока учащимся задаются теоретические вопросы. Тот ученик, у которого находится карточка с ответом, поднимает руку и зачитывает его. Так в течение 3–5 минут учащиеся ежедневно повторяют теоретический материал по математике. Ниже приведены примеры заданий, вопросов и ответы к ним.

ЗАДАНИЯ И ВОПРОСЫ

1. Назовите компоненты сложения.

 2. Назовите компоненты вычитания.

3. Как найти неизвестное слагаемое?

4. Как найти неизвестное уменьшаемое?

5. Как найти неизвестное вычитаемое?

13. Что значит прибавить к числу 1?

14. Что значит вычесть из числа 1?

ОТВЕТЫ

 1. Первое слагаемое, второе слагаемое, сумма.

 2. Уменьшаемое, вычитаемое, разность. 3.

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

4. Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

5. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

13. Прибавить к числу 1 — это значит назвать следующее число.

Например: 6 + 1 = 7

 14. Вычесть 1 — это значит назвать предыдущее число.

 Например: 8 – 1 = 7

 

Статья

Начальная школа выпуск 6 2006 год страница 58

https://n-shkola.ru/storage/archive/1407237288-999777803.pdf

Статья

Начальная школа выпуск 7 2006 год страница 72

https://n-shkola.ru/storage/archive/1407237598-608984697.pdf

С.Н. Числова. Интегрированный урок математики в условиях коррекционно - развивающего обучения

Анализ школьной программы позволил нам систематизировать имеющиеся и составить собственные арифметические задачи, использование которых должно помочь учителю в организации интегрированных уроков по математике и ознакомлению с окружающим миром (по естествознанию).

Приведем примеры таких задач.

 I класс

1. Купальный сезон в летнее время открывается при температуре воды +20 °С, а заканчивается, когда температура воды снижается на 6 °С относительно первоначальной. При какой температуре воды завершается купальный сезон? Почему в конце лета можно купаться при более низкой температуре? Какие способы закаливания вы знаете?

2. Бабушка сказала внуку: «Древние греки называли бабочек ожившими цветами», а затем спросила: «В вазе 5 пионов, а над вазой порхает на 2 оживших цветка больше. Сколько бабочек порхает над вазой с пионами?»

3. Коля поймал в реке 3 карася, а окуней на 2 больше. Сколько окуней поймал Коля? Какая рыба водится в вашей реке?

4. На околоземной орбите вращалось 13 метеорологических спутников. Два столкнулись с метеоритами и сгорели. Сколько спутников осталось?

5. Катя собирала грибы. На поляне она увидела 3 мухомора, 2 сыроежки и 5 рыжиков. Катя собрала только съедобные грибы. Сколько грибов собрала Катя? Какие из перечисленных грибов не являются съедобными?

6. Толя и Сережа должны записать названия деревьев, растущих в парке. Толя написал 4 названия: дуб, ясень, береза, липа. Сережа кроме перечисленных написал еще 2 названия: ольха и жасмин. Все ли из перечисленных мальчиками растений относятся к деревьям? На сколько больше названий деревьев написал Сережа, чем Толя? А какие деревья растут в парке около вашего дома?

 

Статья

Начальная школа выпуск 9 2006 год страница 90

https://n-shkola.ru/storage/archive/1407237323-1378597226.pdf

Статья

Начальная школа выпуск 9 2006 год страница 91

https://n-shkola.ru/storage/archive/1407237323-1378597226.pdf

Статья

Начальная школа выпуск 1 2007 год страница 66

https://n-shkola.ru/storage/archive/1407235628-1251422558.pdf

Статья

Начальная школа выпуск 1 2007 год страница 111

https://n-shkola.ru/storage/archive/1407235628-1251422558.pdf

Статья

Статья

Статья

Статья

Статья

Статья

Статья

Статья

Статья

Статья

Статья

Статья

Статья

Статья

Pdf (n-shkola.ru)

Г.Г. Шмырёва «Работа со схемой в ходе подготовки к решению задач»

В обучении младших школьников математике большая роль отводится текстовым задачам, которые составляют примерно 40 % материала соответствующих учебников. Это связано с тем, что через решение задач реализуются не только образовательные, но и развивающие и воспитательные цели учебного процесса.

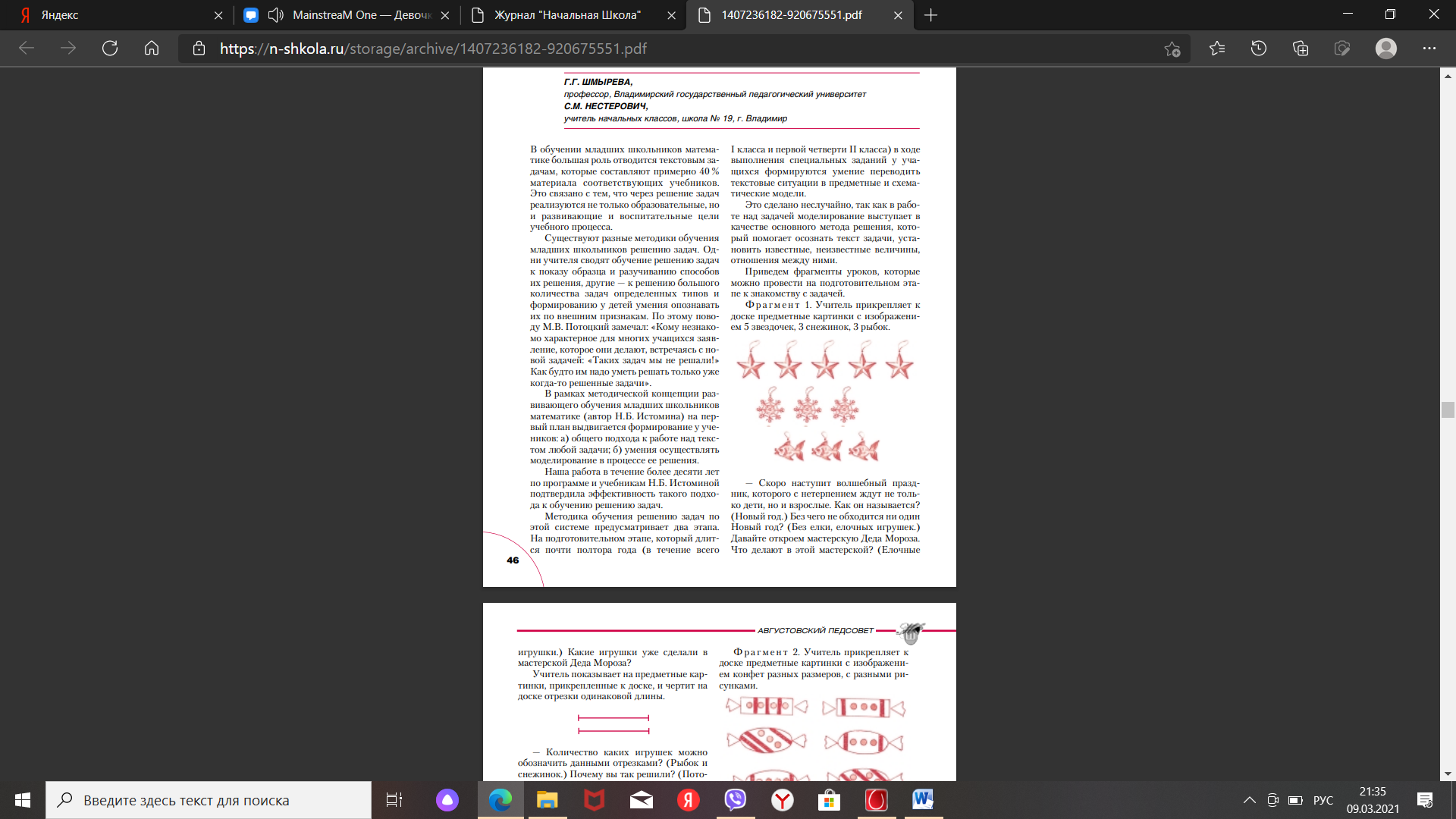
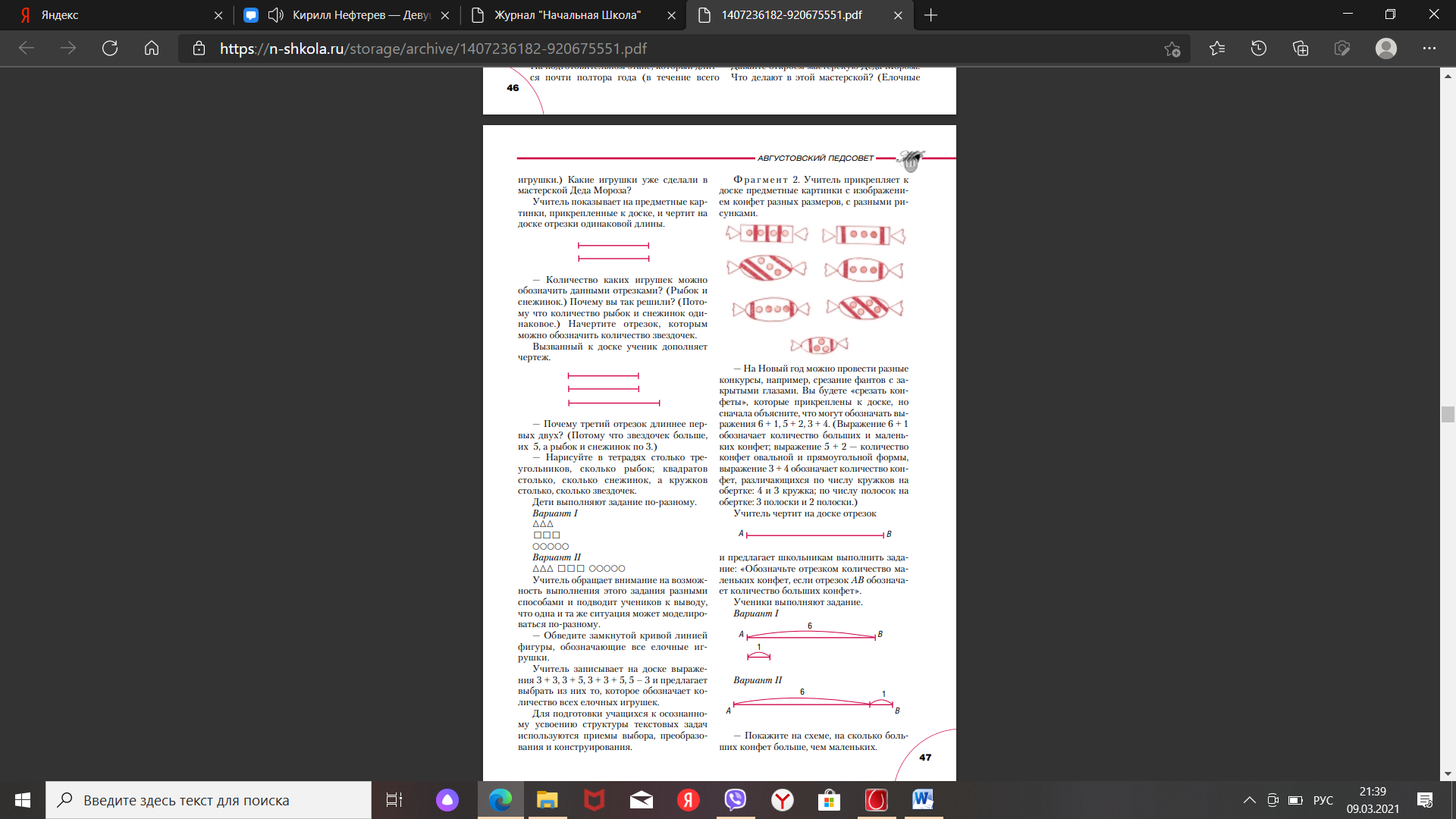
Приведем фрагменты уроков, которые можно провести на подготовительном этапе к знакомству с задачей.

Ф р а г м е н т 1. Учитель прикрепляет к доске предметные картинки с изображением 5 звездочек, 3 снежинок, 3 рыбок.

— Скоро наступит волшебный праздник, которого с нетерпением ждут не только дети, но и взрослые. Как он называется? (Новый год.) Без чего не обходится ни один Новый год? (Без елки, елочных игрушек.) Давайте откроем мастерскую Деда Мороза. Что делают в этой мастерской? (Елочные игрушки.)

Какие игрушки уже сделали в мастерской Деда Мороза? Учитель показывает на предметные картинки, прикрепленные к доске, и чертит на доске отрезки одинаковой длины.

— Количество каких игрушек можно обозначить данными отрезками? (Рыбок и снежинок.) Почему вы так решили? (Потому что количество рыбок и снежинок одинаковое.) Начертите отрезок, которым можно обозначить количество звездочек. Вызванный к доске ученик дополняет чертеж.

— Почему третий отрезок длиннее первых двух? (Потому что звездочек больше, их 5, а рыбок и снежинок по 3.) — Нарисуйте в тетрадях столько треугольников, сколько рыбок; квадратов столько, сколько снежинок, а кружков столько, сколько звездочек. Дети выполняют задание по-разному.

 

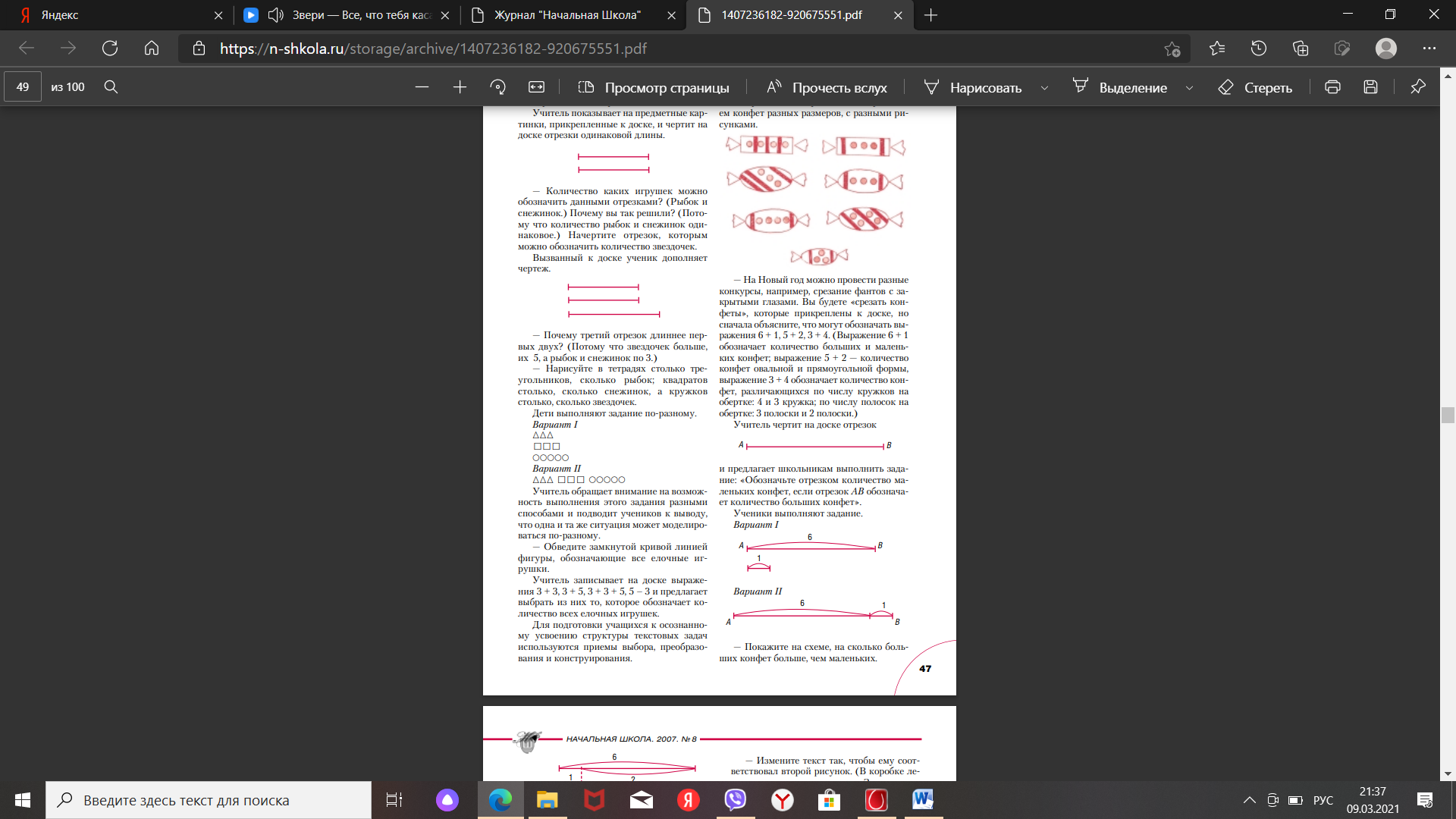
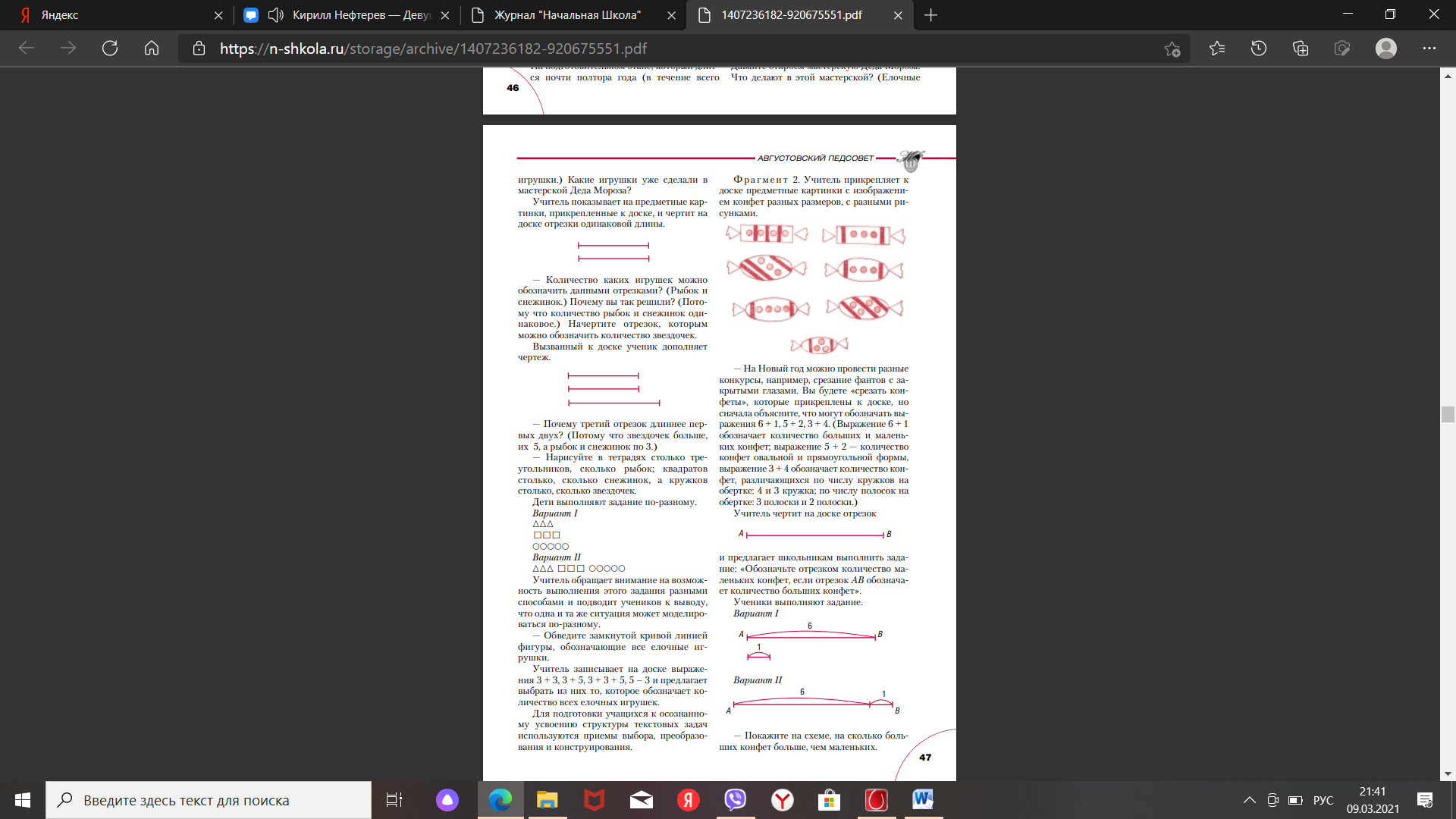
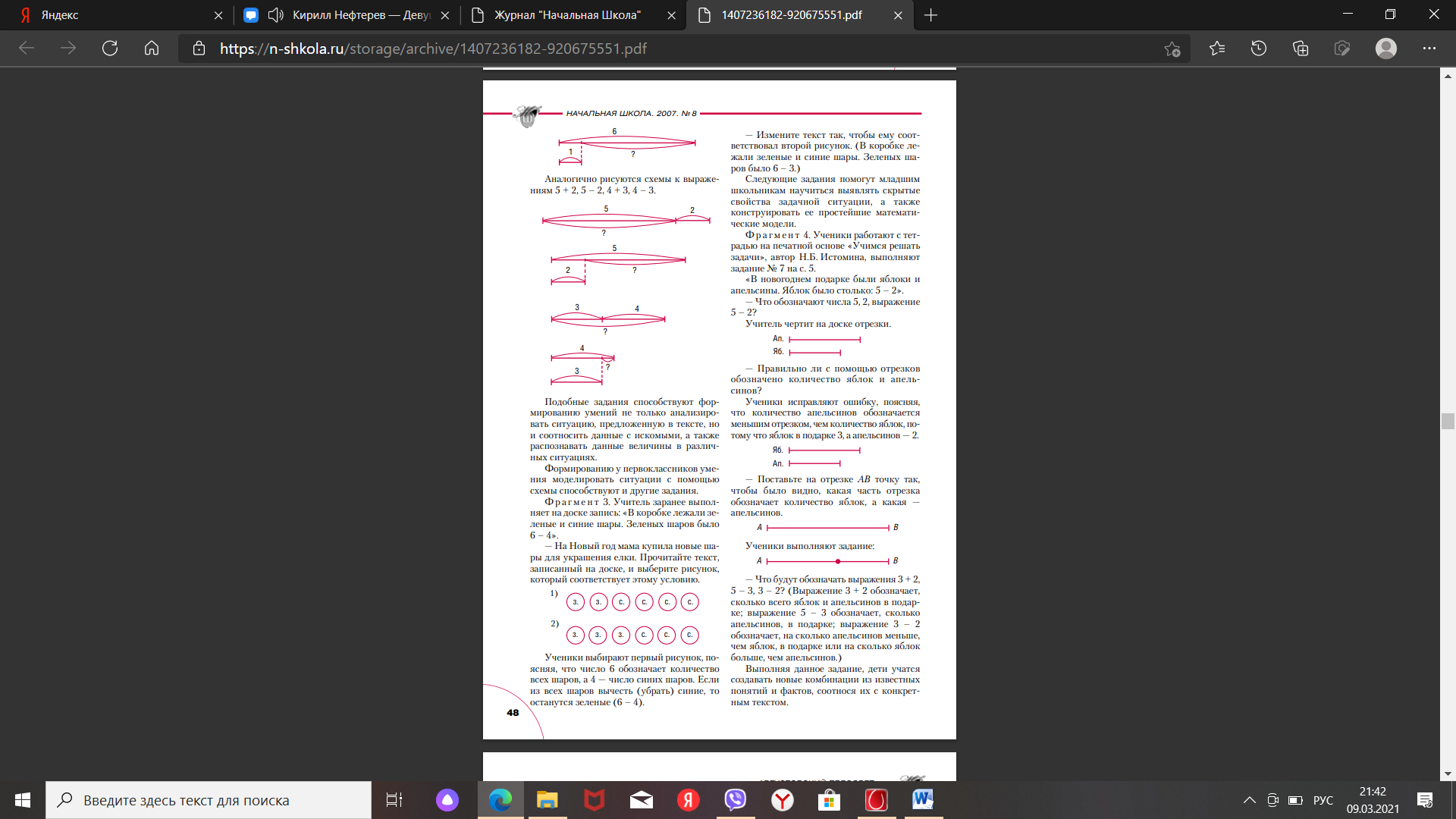
Учитель обращает внимание на возможность выполнения этого задания разными способами и подводит учеников к выводу, что одна и та же ситуация может моделироваться по-разному. — Обведите замкнутой кривой линией фигуры, обозначающие все елочные игрушки. Учитель записывает на доске выражения 3 + 3, 3 + 5, 3 + 3 + 5, 5 – 3 и предлагает выбрать из них то, которое обозначает количество всех елочных игрушек. Для подготовки учащихся к осознанному усвоению структуры текстовых задач используются приемы выбора, преобразования и конструирования.

Ф р а г м е н т 2. Учитель прикрепляет к доске предметные картинки с изображением конфет разных размеров, с разными рисунками.

— На Новый год можно провести разные конкурсы, например, срезание фантов с закрытыми глазами. Вы будете «срезать конфеты», которые прикреплены к доске, но сначала объясните, что могут обозначать выражения 6 + 1, 5 + 2, 3 + 4. (Выражение 6 + 1 обозначает количество больших и маленьких конфет; выражение 5 + 2 — количество конфет овальной и прямоугольной формы, выражение 3 + 4 обозначает количество конфет, различающихся по числу кружков на обертке: 4 и 3 кружка; по числу полосок на обертке: 3 полоски и 2 полоски.) Учитель чертит на доске отрезок

и предлагает школьникам выполнить задание: «Обозначьте отрезком количество маленьких конфет, если отрезок АВ обозначает количество больших конфет». Ученики выполняют задание. В

 

Статья

Pdf (n-shkola.ru)

Статья

И.Г. БОРИСОВА «Математика»

 

 

 

Статья

Статья

Александрова Софья НОЛк-219

Статьи

Статья

Начальная школа выпуск 5 2006 год страница 88

https://n-shkola.ru/storage/archive/1407237212-1332344965.pdf