
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равноускоренный подъем грузаСодержание книги
Поиск на нашем сайте
Рассмотрим вариант подъема груза с помощью троса длиной На данной схеме Рассмотрим действие динамической силы: Статическое напряжение (при равномерном подъеме груза) определяется зависимостью:
Рис. 8.1
Динамическое напряжение:
где Таким образом, эффект динамического воздействия больше статического, а т.к. допускаемые напряжения не связаны с характером динамически сил, то:
РАСЧЕТ ОБОДА МАХОВИКА Обод с радиусом Выделим бесконечно малый элемент обода длиной
Рис. 8.2 Рис. 8.3.
где Однако:
После подстановки в формулу (8.3) получим:
Как известно из курса теоретической механики нормальное ускорение может быть найдено по формуле
Запишем условие равновесия для половины обода маховика (рис. 8.4).
Рис. 8.4
Интенсивность действия распределенной нагрузки может быть найдена по формуле:
Подставим в выражение (8.6) выражения (8.4) и (8.5):
Усилия
Откуда:
Динамическое напряжение может быть определено по формуле:
НАПРЯЖЕНИЯ ПРИ УДАРЕ
Если груз, двигаясь с некоторой скоростью, приходит в соприкосновение с неподвижной системой, то это явление называется ударом. При этом предполагается, что удар неупругий, т.е. груз после соприкосновения с системой движется совместно с ней. В тот момент, когда скорость перемещения груза становится равной 0, деформации конструкции и напряжения в ней достигают своих наибольших значений. Целью расчета на удар является определение наибольших деформаций и напряжений. В основе приближенной теории удара, рассматриваемой в курсе сопротивления материалов, лежит гипотеза о том, что эпюра перемещений системы от воздействия груза Рассмотрим падение груза
Рис. 8.5
Эпюра от действия статической нагрузки изображена на рисунке 8.6.
Рис. 8.6
Из рисунков видно, что эпюра перемещений системы от груза
где Тогда работа, совершаемая грузом при падении с высоты
В момент, когда деформации системы достигают максимального значения, скорости движения груза и системы, а, следовательно, и их кинетическая энергия, равны 0. Потенциальная энергия упругой системы равна:
Динамическое усилие можно получить путем перемножения статического действия силы
Тогда потенциальная энергия деформированной системы определяется зависимостью:
Приравняем правые части выражений (8.9) и (8.10):
или Согласно формуле (8.8)
Тогда: Разделим левую и правую часть полученной зависимости на
Напряжения при ударе связаны со статическими напряжениями величиной:
откуда: Таким образом, динамические напряжения всегда больше статических на величину Для определения наибольших напряжений и перемещений при ударе, напряжения и перемещения, найденные при расчете системы от силы Вопросы для самопроверки К разделу 8 1. Какие нагрузки называются статическими, и какие – динамическими? 2. В чем заключается принцип Даламбера? 3. Какова величина динамического коэффициента при равноускоренном подъеме груза? 4. Как выглядит формула для расчета динамических напряжений при расчете обода маховика? 5. Какое явление называется ударом? 6. Какая гипотеза лежит в основе приближенной теории удара, рассматриваемой в курсе сопротивления материалов? 7. Как связаны наибольшие напряжения и перемещения при ударе с напряжениями и перемещениями, найденными при расчете системы от той же силы, действующей статически? 8. Что называется динамическим коэффициентом при ударе? ГИДРАВЛИКА Гидравлика – прикладная техническая дисциплина, в которой рассматриваются законы равновесия и движения жидкости в инженерных объектах, а также применение этих законов для решения технических задач. В гидравлике рассматривают только капельные жидкости, т.е. вещества, находящиеся в данный момент в жидком состоянии. Гидравлика делится на: гидростатику – учение о равновесии жидкости; и гидродинамику – учение о движении жидкости. Основные свойства жидкостей: Жидкость представляет собой физическое тело, в котором силы межмолекулярного сцепления меньше, чем у твердого тела, чем обусловлена большая проводимость молекул жидкости. Малые силы, воздействующие на жидкость способны вызвать изменение ее формы. В отличие от твердых тел, жидкость не имеет собственной формы и принимает форму сосудов, в которых она находится, т.е. обладает свойством текучести. Основные параметры жидкости: объемный вес, сжимаемость, температурное расширение, вязкость. Объемный вес Все жидкости обладают свойствам сжимаемости, т.е. способностью уменьшаться в объеме под действием сжимающих сил. Коэффициент объемного сжатия Коэффициент
Вязкость – свойство жидкости, заключающееся в наличии сил трения между движущимися соседними слоями. Проявляется только в процессе движения жидкости, вдоль твердой поверхности. Может быть измерено величиной касательного межслоевого напряжения. Данное напряжение тем больше, чем больше относительная скорость движения соседних слоев.
Рис. 9.1
Поле скоростей в потоке вязкой жидкости показано на рисунке 9.1. Экспериментально установлено, что для основной массы жидкостей наблюдается прямая пропорциональность касательного напряжения сдвига и относительной скорости слоев. Вводя экспериментальный коэффициент Средним гидростатическим давлением называется сила сжатия жидкости, приходящаяся на единицу площади
Такое среднее давление будет существенно отличатся от давления в пределах площадки
Т.о. гидростатическим давлением называется напряжение, возникающее в жидкости в результате действия сжимающих сил. Сжимающаяся сила, приходящаяся на элемент площади dP= pdF, а вся сила, действующая на длинную площадь, может быть найдена интегрированием по площади.
Свойства гидростатического давления: Оно всегда направлено по нормали к поверхности; Гидростатическое давление в данной точке во всех направлениях одинаково; В различных точках, гидростатическое давление жидкости различно и является функцией координат точки. В зависимости от выбора начала отсчета численное значение давления различно. Абсолютное давление отсчитывается от абсолютного нуля, за который принимают давление в пустоте. Если давление отсчитывается от нуля, за который принято атмосферное давление
|
|||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.253.199 (0.011 с.) |

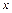 (рис. 8.1).
(рис. 8.1).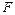 – площадь поперечного сечения троса;
– площадь поперечного сечения троса; 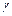 – удельный вес материала троса;
– удельный вес материала троса; 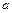 – ускорение при подъеме (груз поднимается равноускоренно).
– ускорение при подъеме (груз поднимается равноускоренно). . (8.1)
. (8.1)
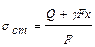 .
.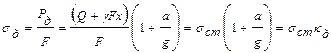 , (8.2)
, (8.2)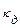 – динамический коэффициент (не может быть меньше 1).
– динамический коэффициент (не может быть меньше 1).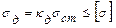 .
.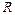 (средний радиус) и площадью поперечного сечения обода
(средний радиус) и площадью поперечного сечения обода 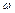 . Влиянием спиц пренебрегаем (рис. 8.2).
. Влиянием спиц пренебрегаем (рис. 8.2).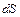 (рис. 8.3). При движении сила инерции направлена от центра. Масса выделенного элемента может быть найдена по формуле:
(рис. 8.3). При движении сила инерции направлена от центра. Масса выделенного элемента может быть найдена по формуле: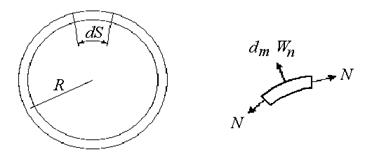
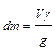 , (8.3)
, (8.3)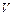 – объем элемента,
– объем элемента, 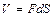 .
.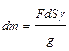 . (8.4)
. (8.4)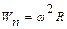 . (8.5)
. (8.5)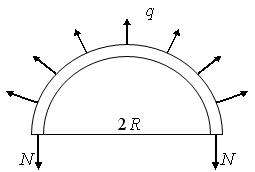
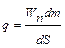 . (8.6)
. (8.6)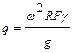 .
.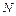 противодействуют распределенной нагрузке, следовательно:
противодействуют распределенной нагрузке, следовательно: .
.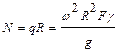 .
. . (8.7)
. (8.7) при ударе подобна эпюре перемещений, возникающих от этого же груза, но действующего статически.
при ударе подобна эпюре перемещений, возникающих от этого же груза, но действующего статически.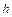 на двухопорную балку. Эпюра наибольших динамических прогибов изображена на рисунке 8.5.
на двухопорную балку. Эпюра наибольших динамических прогибов изображена на рисунке 8.5.

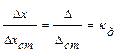 , (8.8)
, (8.8) – наибольшая деформация по направлению груза
– наибольшая деформация по направлению груза 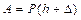 .
.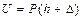 . (8.9)
. (8.9)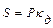 .
.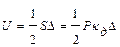 . (8.10)
. (8.10)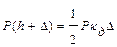 ,
,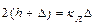 . (8.11)
. (8.11)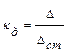 . После подстановки в (8.11) получаем:
. После подстановки в (8.11) получаем: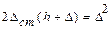 .
.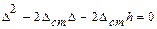 .
.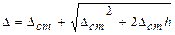 .
.  , тогда:
, тогда: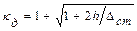 . (8.12)
. (8.12)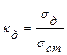 ,
, . (8.13)
. (8.13) .
.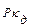 .
.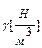 плотность
плотность 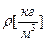
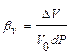 , где
, где  - начальный объем жидкости,
- начальный объем жидкости,  - его изменение под влиянием изменения давления dP.
- его изменение под влиянием изменения давления dP.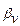 имеет очень малые значения. Для изменения объема газа в 2 раза нужно приложить давление 2200 атмосфер. Температурное расширение – аналогичное понятие.
имеет очень малые значения. Для изменения объема газа в 2 раза нужно приложить давление 2200 атмосфер. Температурное расширение – аналогичное понятие. . Величина
. Величина 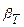 значительно больше
значительно больше 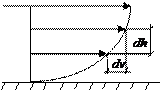
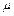 (динамический коэффициент вязкости) можно получить зависимость
(динамический коэффициент вязкости) можно получить зависимость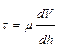 .
.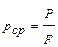 .
.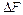 и тем больше, чем больше площадка
и тем больше, чем больше площадка 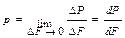 .
.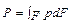 .
.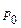 , оно называется избыточным
, оно называется избыточным  . Отрицательное избыточное давление будет тогда, когда абсолютное давление меньше атмосферного. Такое давление называется отрицательным избытком под атмосферой или вакуумом
. Отрицательное избыточное давление будет тогда, когда абсолютное давление меньше атмосферного. Такое давление называется отрицательным избытком под атмосферой или вакуумом 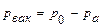 .
.


