
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Касательные напряжения при изгибеСодержание книги
Поиск на нашем сайте
При чистом изгибе в поперечном сечении бруса действует только изгибающий момент и, следовательно, возникают только нормальные напряжения. В случае поперечного изгиба в сечении бруса действуют наряду с изгибающими моментами перерезывающие силы Касательные напряжения распределены по сечению неравномерно, поэтому угловые смещения также распределяются по сечению неравномерно. В связи с этим при поперечном изгибе, в отличие от чистого изгиба, поперечные сечения не остаются плоскими. Однако на величине нормальных напряжений искажение плоскости поперечных сечений сказывается незначительно, поэтому гипотезу плоских сечений можно считать применимой и при поперечном изгибе.
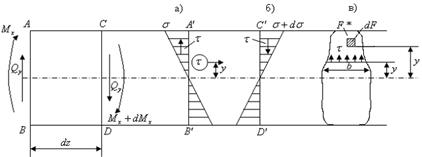
Рис. 5.12
Определим приблизительно касательные напряжения На левую часть элемента действует изгибающий момент Повернутое на Равнодействующая нормальных сил в левом сечении в пределах отсеченной части
Однако, зная что
то после подстановки в уравнение (4.9), получим
где Полученный интеграл – статический момент относительно горизонтальной оси части площади, расположенной выше продольного сечения (выше уровня
В правом сечении продольная сила определяется зависимостью
Разность этих двух усилий
Она должна уравновешиваться касательными силами, возникающими в продольном сечении элемента
или формула Журавского
Данное выражение позволяет вычислять касательное напряжение, возникающее в продольном сечении стержня, а также в его поперечном сечении (с учетом закона парности касательных напряжений). Закон парности касательных напряжений: по двум взаимно перпендикулярным площадкам действуют равные по величине и противоположные по направлению касательные напряжения. Зависимость от расстояния до нейтральной оси, представленная в формуле Журавского, не носит линейного характера, так как она представлена в неявном виде в величине По формуле (5.10) определяется лишь абсолютное значение касательного напряжения; знак этого напряжения совпадает со знаком перерезывающей силы, действующей в рассматриваемом сечении.
|
||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 79; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.53.7 (0.009 с.) |

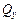 . В связи с этим в поперечных сечениях возникают не только нормальные напряжения, но и касательные напряжения
. В связи с этим в поперечных сечениях возникают не только нормальные напряжения, но и касательные напряжения 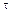 . Их возникновение сопровождается появлением угловых деформаций, поэтому каждая элементарная площадка получает угловые смещения, обусловленные сдвигом.
. Их возникновение сопровождается появлением угловых деформаций, поэтому каждая элементарная площадка получает угловые смещения, обусловленные сдвигом.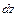 .
.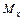 , на правую – изгибающий момент
, на правую – изгибающий момент 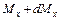 , а также перерезывающая сила
, а также перерезывающая сила 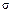 и касательное
и касательное 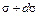 и касательное
и касательное 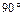 левое сечение ("лицом" к нам) показано на
левое сечение ("лицом" к нам) показано на 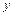 от нейтральной оси, и рассмотрим условие равновесия верхней отсеченной части.
от нейтральной оси, и рассмотрим условие равновесия верхней отсеченной части.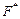 определяется как сумма проекций на ось
определяется как сумма проекций на ось 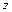 (см. вывод формулы нормальных напряжений):
(см. вывод формулы нормальных напряжений):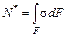 . (5.9)
. (5.9)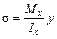 ,
,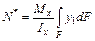 ,
,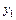 – текущая ордината площадки
– текущая ордината площадки 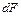 .
.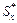 . Тогда,
. Тогда,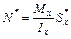 .
.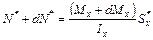 .
.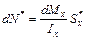 .
.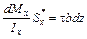 ,
,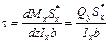 . (5.10)
. (5.10)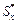 , поэтому характер изменения касательных напряжений по высоте балки криволинеен. В каждом конкретном случае для вычисления величины
, поэтому характер изменения касательных напряжений по высоте балки криволинеен. В каждом конкретном случае для вычисления величины 


