
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система сходящихся сил. Условие равновесия сходящихся силСодержание книги
Поиск на нашем сайте
УДК 531(0758) Ж12я72 ББК С-291
Р е ц е н з е н т ы
Зав. кафедрой «Прикладная геометрия и компьютерная графика», д.т.н., профессор С.И. Лазарев ООО «ОТИХ» Генеральный директор Тишкин П. Г.
УДК 531(0758) Ж12я72 ББК С-291
ГОУ ВПО "Тамбовский государственный технический университет"
Ю.Т. Селиванов ПРИКЛАДНАЯ МЕХАНИКА
Учебное пособие для студентов дневного и заочного отделений специальностей 15.03.02, 15.03.05, 18.03.02, 19.03.01, 19.03.02, 20.03.01, 22.03.01, 28.03.02, 29.03.03
Тамбов Издательство Тгту 2017
УДК 531(0758) Ж12я72 ББК С-291 ПРИКЛАДНАЯ МЕХАНИКА Селиванов Ю.Т. ВВЕДЕНИЕ Прикладная механика для специальностей 15.03.02, 15.03.05, 18.03.02, 19.03.01, 19.03.02, 20.03.01, 22.03.01, 28.03.02 и 29.03.03 включает в себя разделы из следующих дисциплин: Теоретическая механика, Сопротивление материалов и Гидравлика. Изучение указанных разделов необходимо для формирования следующих компетенций:ПК-5 (способность принимать участие в работах по расчету и проектированию деталей и узлов машиностроительных конструкций в соответствии с техническими заданиями и использованием стандартных средств автоматизации проектирования); ПК-5 (способность использовать методы расчетов элементов технологического оборудования по критериям работоспособности и надежности); ОПК-1 (готовность к изменению вида и характера профессиональной деятельности, работе над комплексными проектами); ОПК-1, ОПК-2 (способность и готовность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования); ОПК-2 (готовность использовать знания о современной физической картине мира, пространственно-временных закономерностях, строении вещества для понимания окружающего мира и явлений природы); ОПК-3 (способность использовать основные естественнонаучные законы для понимания окружающего мира и явлений природы); ОПК-3 (готовность применять фундаментальные математические, естественнонаучные и общеинженерные знания в профессиональной деятельности); ОПК-4 (способность обосновывать принятие технического решения при разработке проекта, выбирать технические средства и технологии, в том числе с учетом экологических последствий их применения); ПКВ-13 (способность использовать методы расчета на основе прикладной механики). Основные понятия теоретической механики следующие: Механическим движением называется перемещение материальных тел в пространстве и времени относительно друг друга. Состояние равновесия – частный случай механического движения. Материальной точкой называется тело конечной массы, обладающее размерами, гораздо меньшими, чем другие тела или расстояния между ними. Системой материальных точек называется совокупность материальных точек, связанных между собой определенной зависимостью в перемещении и времени. Абсолютно твердым телом называется материальное тело, расстояние между любыми двумя точками которого остается неизменным при любых воздействиях на это тело. Статика – раздел механики, в котором изучаются методы преобразования системы сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу. СТАТИКА ОСНОВНЫЕ ПОНЯТИЯ СТАТИКИ Сила – мера механического взаимодействия тел друг на друга, определяющая интенсивность и направление этого взаимодействия. Это векторная величина, определяемая тремя элементами: 1) Числовым значением (модулем) 2) Направлением 3) Точкой приложения Прямая, по которой действует сила, называется линией действия силы. Сила измеряется в Ньютонах [Н], килограммах [кг], тоннах [т]. 1[кг]=10[Н] Совокупность нескольких сил, действующих на данное тело, называется системой сил. Тело может находиться в состоянии покоя или движении определенного характера (по определенному закону) – это кинематическое состояние точки или тела. Если на тело действуют различные системы сил, и кинематическое состояние тела не изменяется при действии каждой из них, такие системы называются эквивалентными. Сила, эквивалентная некоторой системе, называется равнодействующей. Сила, равная по модулю равнодействующей и противоположно направленная, называется уравновешивающей. Силы, действующие на механическую систему, делятся на внешние и внутренние: Внешние – результаты взаимодействия различных тел. Внутренние – результат взаимодействия между материальными точками рассматриваемой системы. Силы разделяют на сосредоточенные (когда размеры площадки воздействия гораздо меньше размеров элемента); и распределенные (на протяжении длинны или площадки). Различают равномерно и неравномерно распределенные. По длительности воздействия: постоянные силы (все время существование конструкции) и временные. По характеру воздействия: статические (т.е. неизменные во времени) и динамические. Основная задача статики: Исследование условий равновесия внешних сил, приложенных к абсолютно твердому телу.
СВЯЗИ. РЕАКЦИИ СВЯЗЕЙ Тело, ограничивающее свободу движения твердого тела, является по отношению к нему связью. Реакция связи – сила, воздействующая на рассматриваемое тело со стороны связи. Принцип освобождения от связи: несвободное тело можно рассматривать как свободное, на которое кроме заданных сил действуют реакции связей. 1) Гладкие поверхности (рис. 1.1).
Рис. 1.1 2)
Рис. 1.2 3) Гибкие связи (нить, трос, канат). Реакция действует вдоль оси нити (связи) (рис. 1.3).
Рис. 1.3 4) Стержни. Реакция действует вдоль оси стержня (рис. 1.4).
5) Шарнирно – неподвижная опора (подшипник) (рис. 1.5). Реакция проходит через центр шарнира, но ее модуль и направление не известны.
Рис. 1.5 В общем случае рассчитываются две составляющие реакции
Рис. 1.6 6) Шарнирно – подвижная опора (подшипник на катках) (рис. 1.7). Реакция действует в вертикальном направлении.
Рис. 1.7
7) Жесткая заделка (рис. 1.8). Возникают три реакции: две силы
ПАРА СИЛ. МОМЕНТ ПАРЫ СИЛ Система двух, равных по модулю, параллельных и противоположно направленных, называется парой сил (рис. 1.9). Плоскость, в которой находятся линии действия этих двух сил, называется плоскостью действия пары сил. Пара сил не имеет равнодействующей, но силы пары не уравновешиваются, т.к. они не направлены по одной прямой. Пара сил стремится произвести вращение твердого тела, к которому оно приложено. Т.к. пара сил не имеет равнодействующей, она не может быть уравновешенна силой.
Рис. 1.9 Кратчайшее расстояние d между линиями действия сил, составляющих пару, называющейся плечом пары сил. Действие пары сил на твердое тело характеризуется ее моментом. Момент пары сил определяется произведением модуля одной из них на плечо d:
Если сила измеряется в Ньютонах, а плечо в метрах, то момент пары сил выражается в Н Теорема о парах:Пару сил, не изменяя действия на твердое тело можно переносить в любое место в плоскости ее действия, поворачивать ее плечо на любой угол, а также изменять это плечо и модули сил, не изменяя числового значения величины ее момента и направления вращения. АКСИОМЫ СТАТИКИ Они сформулированы на основе законов механики Галилея – Ньютона: 1. Аксиома инерции. Под действием взаимно уравновешивающихся сил, материальная точка находится в состоянии покоя или движется равномерно. 2. Аксиома равновесия двух сил. Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны, и они направлены по одной прямой в противоположные стороны. 3. Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твердое тело не изменится, если к нему присоединить или из него исключить систему взаимно уравновешивающихся сил. Следствие: не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии её действия, сохраняя неизменными её модуль и направление. 4. Аксиома параллелограмма сил. Равнодействующая двух взаимно пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах (рис. 1.10).
Рис. 1.10 Модуль равнодействующей силы:
5. Аксиома равенства действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие. Рис. 1.11
Перенесем эти силы в точку А в соответствии со следствием третьей аксиомы. Получим вариант, соответствующий четвертой аксиоме. 2) Случай многоугольника сил (рис. 1.12). Пусть к твердому телу в точках
Рис. 1.12 Все эти силы можно перенести в точку О пересечения их линий действия и, строя параллелограммы сил последовательно, сложить их, получая силы Если сил больше трех, удобно применить аналитический метод. При решении графическим методом, рассмотренном выше.
. При аналитическом решении задается система координат и складываются проекции сил
.
Например,
Рис. 1.13
Условие равновесия системы сходящихся сил: Для того, чтобы тело было в равновесии необходимо и достаточно, чтобы равнодействующая была равна 0, т.е. геометрическая сумма всех сил, приложенных к телу = 0. Для случая многоугольника: сходящиеся силы уравновешиваются в случае, если их равнодействующая = 0, т.е. многоугольник замкнут (рис. 1.14).
Рис. 1.14 В замкнутом многоугольнике сил все силы направлены по контуру многоугольника в одну сторону по обходу многоугольника. Для трех сил: три сходящиеся силы уравновешиваются, если треугольник сил замкнут (рис. 1.15).
Рис. 1.15
Рис. 1.16 Способ заключается в том, что мысленно вырезают узлы фермы, прикладывают к ним внешние силы и реакции в стержнях и составляют уравнения равновесия сил, приложенных к каждому узлу, Т.к. в начале неизвестно какие стержни растянуты, а какие сжаты, то условно предполагают, что все стержни растянуты (реакции направлены от узлов), если в результате вычислений получают результат с минусом, то стержень сжат. Последовательность рассмотрения узлов определяется условием, что число неизвестных сил, приложенных к узлу не должно превышать числа уравнений равновесия сил (для плоских 2). Неизвестные определяются из уравнений статики. Правильность вычислений можно проверить построив многоугольники сил, приложенных к узлам. Эти многоугольники должны быть замкнутыми. ТРЕНИЕ Если к твердому телу, покоящемуся на шероховатой горизонтальной поверхности приложить горизонтальную силу S, то действие этой силы вызовет силу трения (рис. 1.17).
Рис. 1.17 . (1.4) Он зависит от материала тела и физического состояния соприкасающихся поверхностей и определяется экспериментально. Его величина обычно меньше единицы. Угол, тангенс которого равен коэффициенту трения скольжения называется углом трения. Это максимальный угол между силами
Вопросы для самопроверки К разделу 1 1. Что такое материальная точка? 2. Что такое абсолютно твердое тело? 3. Что называется моментом силы относительно данной точки и какова его размерность? 4. Что называется реакциями связей? 5. Что такое статически эквивалентная система сил? 6. Что такое аксиомы статики твердого тела? Как они формулируются? 7. Какими единицами измеряется сила в Международной системе (СИ)? 8. Перечислите признаки, характеризующие силу. 9. Что называется системой сил? 10. Приведите примеры сосредоточенных и распределенных сил. 11. Что называется равнодействующей системы сил? 12. Какая сила называется уравновешивающей? 13. Дайте определение внешней и внутренней силы. 14. Сформулируйте аксиому о равновесии двух сил. 15. Что такое система сил? 16. Какие системы сил называются эквивалентными? 17. Что такое равнодействующая и уравновешивающая сила? 18. Какие системы сил называются статически эквивалентными? 2. Основные понятия и определения сопротивления материалов Перемещения и деформации
В сопромате расчеты конструкций производят с использованием расчетных схем. На расчетной схеме вместо бруса изображают его ось. Нагрузку, приложенную к небольшим участкам поверхности бруса, заменяют сосредоточенными силами. Нагрузку, приложенную к участкам больших размеров, составляющих существенную часть его длины, изображают распределенной силой (рис. 2.1).
Рис. 2.1 Перемещения возникают за счет деформации тела. В теории предполагается, что у нас действуют только упругие деформации. Известны два вида деформаций: изменение длины и сдвиг (рис. 2.2). В первом случае происходит уменьшение или увеличение длины отрезка. Во втором искажение первоначально прямого угла.
Рис. 2.2
Элемент ABCD расположен в поперечном сечении бруса. Точка А, начало отсчета, считается неподвижной. Внутренние силы в сечении можно разложить на две составляющие: касательную (включает силы расположенные в плоскости сечения) и нормальную (перпендикулярна плоскости сечения). Метод сечений
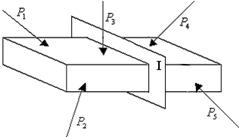
Рассмотрим элемент конструкции, на который действует система внешних сил, находящихся в равновесии (рис. 2.3). Причем в число внешних сил входят как заданные активные силы, так и реакции связи.
Рис. 2.3
Мысленно рассечем элемент плоскостью I. Силы воздействия отсеченной левой части на правую для всего элемента считаются внутренними. На основании известного закона механики (действие равно противодействию), эти силы равны по величине и противоположны по направлению. Каждому из усилий соответствует определенный вид деформации бруса: продольной силе N – растяжение-сжатие, моменту

Рис. 2.4
Все эти усилия являются внутренними. Прием определения этих усилий называется методом сечений. Так как внешние силы уравновешиваются внутренними, то проекция на какую-либо ось внутреннего усилия, действующего со стороны левой части на правую, равна проекции на эту ось всех внешних сил, приложенных к левой части. Момент относительно какой-либо оси внутренних усилий в сечении, действующий со стороны левой части на правую, равен моменту всех внешних сил, действующих со стороны левой части, относительно этой оси.
2.5. Напряжения Внутренние силы в сечении можно разложить на две составляющие: нормальную и касательную. Первая составляющая перпендикулярна плоскости сечения, а вторая расположена в этой плоскости. Напряжение – интенсивность касательных сил в рассматриваемой точке сечения называется касательным напряжением:
где T – касательная сила; F – площадь сечения. Интенсивность нормальных сил называется нормальным напряжением:
Нормальные и касательные напряжения являются составляющими полного напряжения (эквивалентного):
Величины напряжений s и t в каждой точке элемента зависят от направления сечения, проведенного через эту точку, т.е. если сечение расположено по отношению к горизонтальной оси под углом не равным 90°, то величины s и t изменятся. Вопросы для самопроверки К разделу 2 1. В чем заключаются задачи курса «Сопротивление материалов»? 2. Какие гипотезы используются при изучении курса «Сопротивление материалов»? 3. Что называют прочностью, жесткостью, устойчивостью детали? 3. Какие силы в сопротивлении материалов считают внешними? Какие силы являются внутренними? 4. Какими методами определяют внешние силы? Как называют метод для определения внутренних сил? 5. Как классифицируются нагрузки, действующие на части машин и сооружений? 6. Что такое сосредоточенная сила, распределенная нагрузка и момент? 7. Поясните суть метода сечений. 7. Дайте определение понятия «напряжения» и какие виды напряжения вы знаете? 8. В каких единицах измеряются напряжения? 9. Чем отличаются нормальные напряжения от касательных? 10. Что оценивается величиной напряжений?
Рис. 3.1
Из уравнения проекций на вертикальную ось имеем:
где Р – внешняя сила; N – внутреннее усилие. Метод сечений:для нахождения внутренних усилий тело мысленно разрезают на две части и рассматривают равновесие той части, которая не соприкасается с заделкой. При растяжении-сжатии гипотеза плоских сечений дополняется еще одним пунктом: в поперечных сечениях достаточно далеко удаленных от точки приложения сил нормальные силы распределяются по сечению равномерно, а касательные отсутствуют. Нормальное напряжение характеризует величину внутренних усилий приходящихся на единицу площади сечения:
Правило знаков: нормальные усилия и напряжения положительны при растяжении и отрицательны при сжатии. Условие прочности при растяжении и сжатии
где Решая совместно уравнения (3.2) и (3.3), имеем
Это уравнение прочности при растяжении-сжатии. С его помощью возможно решение трех типов задач, но наиболее часто решается задача подбора площади сечения F при известных значениях N и
Например, для круга
Для прямоугольного сечения должно быть задано соотношение сторон:
где h – высота; b – основание. Значение продольной силы в каждом частном случае можно легко определить с помощью метода сечений. Для нахождения напряжения
Рис. 3.5
Линейную деформацию
Происходит также изменение поперечных размеров бруса. Относительная поперечная деформация может быть рассчитана по формуле
Экспериментально установлено, что при напряжениях, не превышающих предела упругости, выполняется уравнение:
где Установлено, что когда напряжение в брусе не превышает предела пропорциональности, выполняется условие
где Е – коэффициент, зависящий от физических свойств материала (модуль упругости). Параметр Е, наряду с m, характеризует упругие свойства материала. Для стали Произведение EF называется жесткостью поперечного сечения бруса а, учитывая что
или
Абсолютное удлинение бруса выражается зависимостью, полученной из (3.6) и (3.7):
Формулы (3.8) – (3.10) являются математическим выражением закона Гука, который звучит так: абсолютная продольная деформация прямо пропорциональна продольной силе (при постоянной жесткости сечения EF); или относительная продольная деформация прямо пропорциональна нормальному напряжению.
Рис. 3.6
Уравнение равновесия в виде суммы проекций на вертикальную ось будет иметь вид
В этом уравнении два неизвестных, следовательно, степень статической неопределимости системы равна единице. Так как стержень жестко заделан по концам, то изменение длины стержня отсутствует:
или
При решении задачи используем метод сечений. По закону Гука:
Решая совместно уравнения (3.13) – (3.16), получим:
Реакцию
Направление неизвестных реакций (3.11) – уравнение равновесия; (3.12), (3.13) – геометрические уравнения совместности деформаций; (3.14), (3.15) – физические уравнения данной задачи (закон Гука); (3.17) – физическое уравнение совместности деформаций. Рис. 3.7
Степень статической неопределимости равна единице:
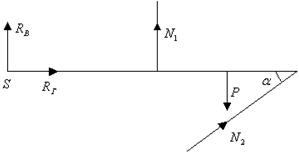
Рис. 3.8
Из уравнения (3.18) необходимо определить правильность направления реакций Для симметричных схем: направления проекций на вертикальную ось реакций Для остальных схем: знаки моментов, создаваемых усилиями 2. Составление схемы деформации (рис. 3.9). 1) Показываем положение схемы в исходном положении:
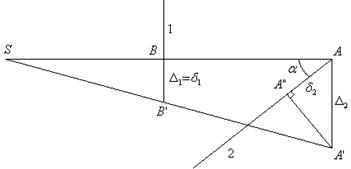
Рис. 3.9
2) Определяем, куда сместится жесткая балка от воздействия внешней силы, и показываем новое положение системы. При этом необходимо сделать два допущения: а) жесткая балка не деформируется; б) перемещение точек приложения стержней A и B происходит не по дугам окружностей, а строго вертикально. Вертикальные перемещения точек приложения стержней обозначим через 3) Из вновь полученных точек 4) Находим соответствие между вертикальными перемещениями
5) Выражаем вертикальные перемещения
Подставим полученные выражения в уравнение (3.19):
3. Выражаем деформации стержней через внутренние усилия в них (закон Гука):
4. Составляем физическое уравнение совместности деформаций, подставив уравнение (3.21) в уравнение (3.20):
Длины стержней Получено недостающее уравнение. Решая его совместно с уравнением (2.21), можно определить усилия 5. После определения 6. Производим проверку правильности решения. 1) В определенном масштабе откладываем длину бруса SBA (рис. 3.10). 2) В точках приложения стержней проводим их линии действия. 3) Откладываем вертикальные перемещения стержней в направлении, соответствующем схеме деформаций (в другом масштабе).
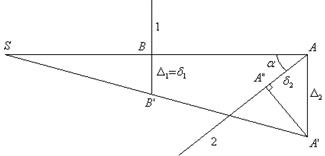
Рис. 3.10 Первая проверка:соединяем точки S, Вторая проверка: из полученных точек 3.5. Напряжения, возникающие в стержневых системах от
Если хотя бы один из стержней шарнирно-стержневой системы вы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.201.240 (0.011 с.) |



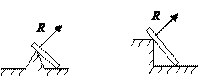 Клин или ребро (рис. 1.2).
Клин или ребро (рис. 1.2).
 Рис. 1.4
Рис. 1.4
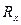 и
и 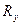 (рис. 1.6).
(рис. 1.6).

 Обозначается:
Обозначается: 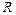
 Рис. 1.8
Рис. 1.8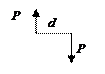
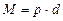 . (1.1)
. (1.1) м.
м.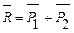 .
.
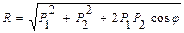 . (1.2)
. (1.2)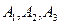 приложены сходящиеся силы
приложены сходящиеся силы 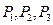

 и т.д. для любого количества сил.
и т.д. для любого количества сил.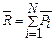
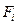 на соответствующие оси (рис. 1.13).
на соответствующие оси (рис. 1.13).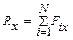 , где
, где 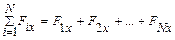
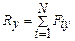
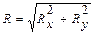 .
.
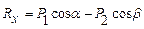
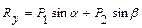 .
.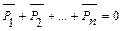 . (1.3)
. (1.3)

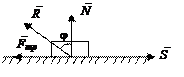
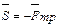
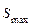 в момент начала движения. Модуль максимальнойсилы трения пропорционален нормальному давлению
в момент начала движения. Модуль максимальнойсилы трения пропорционален нормальному давлению 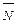 тела на плоскость
тела на плоскость 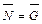 , тогда коэффициент трения определяется зависимостью:
, тогда коэффициент трения определяется зависимостью: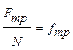 .
.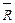 .
.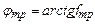 .
.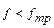 тело находится в покое.
тело находится в покое.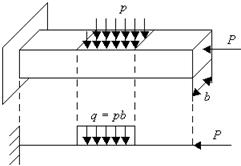

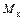 – кручение, моментам
– кручение, моментам 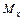 и
и 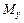 – изгиб (рис. 2.4).
– изгиб (рис. 2.4).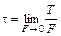 ,
, .
.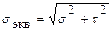 .
. , (3.1)
, (3.1) . (3.2)
. (3.2) , (3.3)
, (3.3)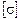 – допускаемое нормальное напряжение (справочная величина, физико-механическая характеристика материала). Это наибольшее напряжение, при котором материал конструкции может надежно и долго работать.
– допускаемое нормальное напряжение (справочная величина, физико-механическая характеристика материала). Это наибольшее напряжение, при котором материал конструкции может надежно и долго работать.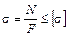 . (3.4)
. (3.4)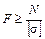 . (3.5)
. (3.5) ;
; 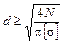 .
.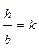 ;
;  ;
;  ,
,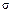 в каждой точке поперечного сечения, необходимо знать закон распределения по сечению, который обычно изображается графиком, показывающим их изменение по высоте балки (эпюра нормальных напряжений).
в каждой точке поперечного сечения, необходимо знать закон распределения по сечению, который обычно изображается графиком, показывающим их изменение по высоте балки (эпюра нормальных напряжений).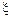 называют относительным продольным удлинением:
называют относительным продольным удлинением: . (3.6)
. (3.6)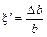 .
.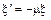 ;
;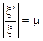 ,
,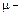 коэффициент поперечной деформации (коэффициент Пуассона), который определяется экспериментально и изменяется в пределах от 0 – для пробки, до 0,5 – для резины; для стали
коэффициент поперечной деформации (коэффициент Пуассона), который определяется экспериментально и изменяется в пределах от 0 – для пробки, до 0,5 – для резины; для стали  .
.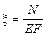 , (3.7)
, (3.7)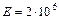 кг/см2; для меди
кг/см2; для меди  кг/см2; для условного дерева
кг/см2; для условного дерева 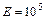 кг/см2.
кг/см2. , (3.8)
, (3.8)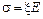 . (3.9)
. (3.9)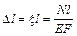 . (3.10)
. (3.10)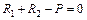 . (3.11)
. (3.11) , (3.12)
, (3.12)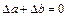 . (3.13)
. (3.13)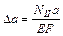 ; (3.14)
; (3.14)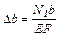 ; (3.15)
; (3.15)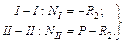 (3.16)
(3.16)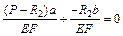 ; (3.17)
; (3.17) ;
; .
.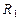 можно определить, подставив полученную величину в уравнение (3.11):
можно определить, подставив полученную величину в уравнение (3.11):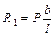 .
.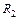 можно принимать произвольно. Если в результате расчета они получились положительными, то направление выбрано верно. Если они получились отрицательными, то необходимо изменить направление указанных реакций:
можно принимать произвольно. Если в результате расчета они получились положительными, то направление выбрано верно. Если они получились отрицательными, то необходимо изменить направление указанных реакций: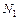 и
и 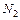 .
.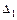 и
и 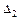 .
.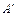 и
и 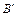 опускаем перпендикуляры на линии действия стержней в исходном состоянии. Обозначим деформации стержней через
опускаем перпендикуляры на линии действия стержней в исходном состоянии. Обозначим деформации стержней через 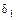 и
и 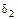 .
.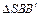 ~
~ 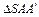 :
: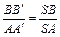 ;
;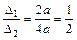 . (3.19)
. (3.19) ;
; ;
;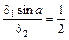 ;
;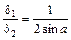 . (3.20)
. (3.20)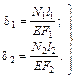 (3.21)
(3.21)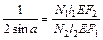 . (3.22)
. (3.22)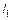 и
и 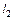 известны. Если дано соотношение площадей
известны. Если дано соотношение площадей 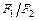 , используя его, сокращаем площади.
, используя его, сокращаем площади.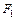 и
и  в соответствии с соотношением, через
в соответствии с соотношением, через  и
и 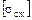 .
.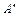 и
и  . Измеренные величины
. Измеренные величины 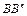 и
и 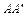 должны быть равны рассчитанным величинам
должны быть равны рассчитанным величинам 


