
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если система сил имеет равнодействующую, то ее момент относительно любой точки или оси равен сумме моментов всех сил системы относительно той же точки или оси.Содержание книги
Поиск на нашем сайте Доказательство Пусть некоторая система сил Рассмотрим любую точку пространства — точку А. I. приведем исходную систему сил Система приводится к одной силе, равной главному вектору, и паре с моментом, равным главному моменту системы сил относительно точки А: II. приведем силу Система приводится к одной силе, равной главному вектору, и паре с моментом равным моменту равнодействующей относительно центра приведения:
Рис. 7.4 Сравнивая результаты приведения систем I и II, мы видим, что силы в них одинаковы и приложены в одной и той же точке A. Поскольку после приведения к центру А эти системы сил останутся эквивалентными, моменты пар также должны быть одинаковы, то есть Это и есть математическая запись теоремы Вариньона. Проецируя равенство (7.5) на оси координат, проходящие через точку А, мы получим выражение теоремы Вариньона для моментов сил относительно осей: Эта теорема часто используется на практике для вычисления момента некоторой силы в том случае, когда сложно найти плечо самой силы, но легко определить плечи ее составляющих.
7.5 ИНВАРИАНТЫ СИСТЕМЫ СИЛ Первым (векторным) инвариантом системы сил является главный вектор, поскольку он не зависит от точки приведения. В отличие от главного вектора главный момент не является инвариантом. При переносе центра приведения из точки О в точку А его величина меняется по закону
где Можно доказать, что при перемене центра не изменяется скалярное произведение главного момента и главного вектора. Действительно, умножив скалярно все слагаемые на главный вектор, получим: Второе слагаемое в правой части равно нулю, поскольку является скалярным произведением взаимно перпендикулярных векторов. Следовательно Таким образом, скалярное произведение главного момента на главный вектор является вторым (скалярным) инвариантом системы сил. Итак, каждая система сил имеет две не зависящие от центра приведения характеристики: 1. векторный инвариант, которым является главный вектор 2. скалярный инвариант, которым является скалярное произведение главного момента на главный вектор. Первый и второй инварианты независимы, то есть из одного из них не следует другой. Иногда в качестве скалярного инварианта системы сил принимают проекцию главного момента на направление главного вектора. Модуль главного вектора не зависит от точки приведения. Поделив на него левую и правую части равенства получим: или где Выражения в левой и правой частях представляют собой проекции главного момента на направление главного вектора. На рис. 7.5 показано, что для различных точек пространства эта величина одинакова, то есть не зависит от выбора центра приведения. Рис. 7.5 7.6. ДИНАМИЧЕСКИЙ ВИНТ, ГЛАВНАЯ ОСЬ СИСТЕМЫ СИЛ По основной теореме статики (§7.2) система сил при приведении к произвольной точке пространства заменяется силой, равной главному вектору, и парой сил с моментом, равным главному вектору системы относительно точки приведения. Для некоторых точек пространства полученные в результате приведения главный вектор и главный момент окажутся коллинеарными, как это показано на рис. 7.5,в. Можно показать, что такие точки будут лежать на одной прямой. Дадим определение:
|
||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

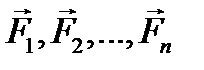 (система I) имеет равнодействующую
(система I) имеет равнодействующую 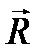 (рис. 7.4), приложенную в точке О (система II). Очевидно, что системы I и II эквивалентны:
(рис. 7.4), приложенную в точке О (система II). Очевидно, что системы I и II эквивалентны: 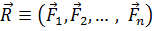 .
.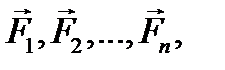 к точке А.
к точке А.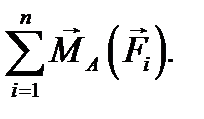
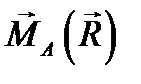 .
.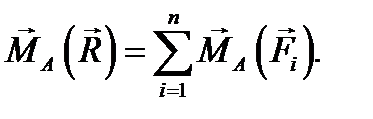 (7.5)
(7.5) (7.6)
(7.6)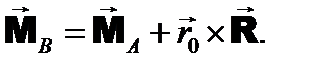 ,
,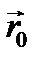 − радиус-вектор, проведенный от нового центра В к точке А.
− радиус-вектор, проведенный от нового центра В к точке А.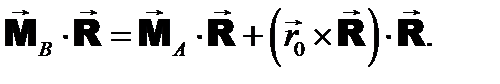
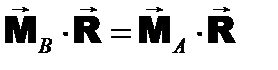 , что и требовалось доказать.
, что и требовалось доказать. ;
;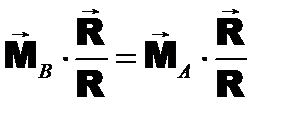
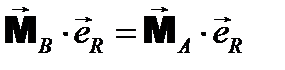 или
или 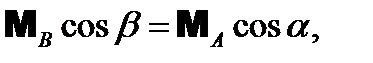
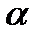 и
и 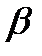 углы между направлениями главного момента и главного вектора соответственно в точках
углы между направлениями главного момента и главного вектора соответственно в точках 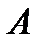 и
и 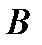 , а вектор
, а вектор 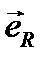 представляет собой единичный направляющий вектор главного вектора.
представляет собой единичный направляющий вектор главного вектора.


