
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет и разделы теоретической механикиСтр 1 из 11Следующая ⇒
Литература, рекомендуемая для изучения статики
Введение Тема 1. ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ 1.1 СИЛЫ И СИСТЕМЫ СИЛ В общем случае твердое тело может находиться или в состоянии покоя, или в состоянии движения. Изменение характера движения происходит под действием сил. Сила − является мерой механического взаимодействия и определяется следующими элементами: · точкой приложения, · направлением, · численным значением (модулем). Важным атрибутом силы является линия действия. Единицей модуля силы является ньютон, хотя на практике используется иногда и другая единица — килограмм силы: 1 кгс = 9,81 Н. Рис. 1.1 Сила является векторной величиной (рис. 1.1). Такие величины мы будем обозначать с чертой или стрелочкой сверху: Условимся, что если черта или стрелка сверху отсутствует, то это означает модуль данного вектора: Совокупность нескольких сил называется системой сил и обозначается следующим образом: Системы сил, оказывающие на свободное твердое тело одинаковое механическое воздействие, называют эквивалентными друг другу. Для обозначения эквивалентности систем сил используются символ
Одна сила, эквивалентная некоторой системе сил, называется ее равнодействующей. Будем обозначать ее символом Заметим, что не всякая система сил имеет равнодействующую. Рассмотрим тело, находящееся в состоянии покоя. Приложим к этому телу некоторую систему сил. Если при этом состояние покоя не нарушилось, будем называть эту систему сил уравновешенной. Про уравновешенную систему сил говорят, что она эквивалентна нулю. Основная задача статики состоит в установлении условий, при которых системы сил являются уравновешенными. Все силы, действующие на точки механической системы (и твердого тела), можно разделить на внешние силы и внутренние силы.
Внешними силами называются силы, с которыми на точки механической системы действуют тела, не входящие в данную систему. Внутренними силами называются силы взаимодействия между объектами механической системы. Деление сил на внешние и внутренние условно, оно зависит от того, какие именно тела мы включаем в данную механическую систему, а какие нет. Например, если рассмотреть подъемный кран и висящий на его тросе груз как одну механическую систему, то сила натяжения троса будет силой внутренней. Если же рассматривать механическую систему, состоящую только из груза, то сила натяжения троса будет является силой внешней.
1.2. АКСИОМЫ СТАТИКИ Перейдем теперь к изложению аксиом статики (положений принимаемых без доказательства), справедливость которых подтверждается всем опытом деятельности человека. Аксиома 1. Аксиома равновесия Система двух сил является уравновешенной только в том случае, когда эти силы: 1) имеют общую линию действия, 2) направлены по ней в противоположные стороны, 3) равны по модулю. Возможных вариантов этого расположения сил всего два, они показаны на рис. 1.2. В обоих случаях имеем: Рис. 1.2 Следствие: · Из данной аксиомы следует, что система из одной силы никогда не может быть уравновешенной. · Если для некоторой системы сил существует эквивалентная ей равнодействующая Аксиома 2. Аксиома эквивалентности Имеют общую линию действия, Равны по модулю. Приведенная формулировка говорит о том, что силы никогда не возникают поодиночке. Действие всегда порождает противодействие. При этом (рис. 1.6): Рис. 1.6 Сравнивая аксиому 4 с аксиомой 1, можно увидеть, что формально силы действия и противодействия образуют уравновешенную систему сил. Однако надо учитывать, что эти силы приложены к разным телам. На основании данной аксиомы можно сделать важное заключение. Свойство внутренних сил Векторная сумма внутренних сил любой механической системы всегда равна нулю.
Действительно, для каждой внутренней силы Приведенное свойство имеет большое значение, поскольку позволяет при составлении уравнений равновесия исключать из рассмотрения неизвестные внутренние силы. Аксиома 5. Принцип отвердевания (замораживания) Тема 2. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
2.1. ПОНЯТИЕ О СВЯЗЯХ Материальные тела взаимодействуя, мешают друг другу перемещаться свободно. Например, если на столе лежит книга, то поверхность стола ограничивает перемещения книги, делая невозможным ее опускание ниже этой поверхности. Также имеются ограничения у положений груза, висящего на тросе: он не может удалиться от точки подвеса на расстояние большее, чем длина троса. Ограничения, наложенные на положения (скорости) точек механической системы, называются связями. Связи всегда осуществляются какими-либо материальными телами. Так, для лежащей на столе книги связь осуществляет поверхность стола; для груза, висящего на тросе, — сам трос. Реакцией связи называется сила, с которой тело, которое осуществляет связь, действует на рассматриваемое тело. Так, для книги, лежащей на столе, реакцией связи будет сила, с которой поверхность стола действует на книгу. Для груза, висящего на тросе, реакцией связи является сила, с которой трос действует на груз (сила натяжения троса). Силы, не являющиеся реакциями связей, принято называть активными. Они, как правило, известны. В технических дисциплинах их часто назавают нагрузками. Реакции связей чаще всего неизвестны. Таким образом, мы имеем теперь два способа классификации сил. Все силы, действующие на механическую систему, делятся на: · внешние и внутренние, · активные силы (нагрузки) и реакции связей. Определение реакций связей, является целью большинства решаемых в статике задач. Большое практическое значение имеет определение сил, действующих на фундаменты, опоры, подвески, расчеты сил натяжения тросов, канатов и прочее. Изучение равновесия несвободных тел основано на следующем принципе: Принцип освобождаемости от связей Тема 3. Заметим, что · Проекции вектора на параллельные оси равны. · Проекции вектора на параллельные плоскости геометрически равны.
3.2. СПОСОБЫ ЗАДАНИЯ СИЛЫ Рассмотрим силу Для указания точки приложения силы используем радиус-вектор
соединяющий начало системы координат и точку приложения силы. Проекции вектора Информация о величине и направлении силы Рис. 3.4 Первый способ Представим вектор силы в виде произведения (рис. 3.4) где
где
Чтобы таким способом задать вектор, необходимо знать углы Второй способ (аналитический) Аналитическое выражение вектора силы дается следующим образом:
где То есть, для аналитического задания вектора силы необходимо указать три его проекции: Тема 4. СХОДЯЩИЕСЯ СИСТЕМЫ СИЛ 4.1. ПРИВЕДЕНИЕ СХОДЯЩЕЙСЯ СИСТЕМЫ СИЛ К РАВНОДЕЙСТВУЮЩЕЙ Сходящейся системой сил называются совокупность сил, линии действия которых пересекаются в одной точке, которую будем называть точкой схода системы. Простейшая система сходящихся сил (две силы) была рассмотрена в аксиоме параллелограмма сил (см. рис. 4.1), где говорилось, что их равнодействующая изображается диагональю параллелограмма, построенного на этих силах, и что она проходит через точку пересечения линий действия исходных сил. Рис. 4.1 Применение аксиомы параллелограмма можно обобщить на случай действия нескольких сходящихся сил. Так, на рисунке 4.2 показано, что при наличии трех сил мы можем сначала определить равнодействующую первых двух сил:
а затем, снова применяя аксиому параллелограмма, найти равнодействующую сил
По мере добавления новых сил можно каждый раз вновь использовать аксиому параллелограмма, предварительно перенося силы в точку схода системы. Каждый раз мы будем получать силу эквивалентную всей системе и, следовательно, являющуюся ее равнодействующей. Рис. 4.2. Линия действия полученной таким образом равнодействующей будет проходить через точку схода системы, а сама она будет равна геометрической сумме сил системы, то есть главному вектору:
Главный вектор, как известно, можно найти либо аналитически, либо путем построения силового многоугольника (рис. 4.2, б) Итак, как показано на рис. 4.3, система сходящихся сил всегда имеет равнодействующую, которая геометрически равна главному вектору этой системы и приложена в точке схода системы. Рис. 4.3 Это справедливо только для сходящихся систем сил. Для других систем сил равнодействующая может определяться иначе. Существуют системы сил, которые вообще не имеют равнодействующей, что означает, что такие системы сил невозможно заменить одной силой. Но нужно помнить, что Тема 5. МОМЕНТЫ СИЛЫ
5.1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ Величина и направление силы характеризуют действие силы в том случае, если она придает какому-либо телу поступательное движение.
Вращательный эффект силы по отношению к некоторой точке или оси учитывает другая характеристика — момент силы. Моментом силы
Рис. 5.1 Направление и модуль момента силы определяются по обычному правилу векторного произведения. Направление момента силы Вектор-момент силы Модуль момента силы Модуль векторного произведения:
или Модуль момента силы относительно точки равен произведению модуля силы на ее плечо. Плечом силы называется кратчайшее (длина перпендикуляра) расстояние от точки до линии действия силы. Единица измерения модуля момента силы [M] = Нм. Из формулы (5.2) следует, что 1. момент силы относительно точки равен нулю только в том случае, когда ее плечо равно нулю, т. е. когда линия действия силы проходит через эту точку; 2. момент силы не зависит от того, где взята точка приложения силы на линии ее действия; 3. модуль момента силы равен удвоенной площади треугольника, для которого сила является основанием, а плечо высотой (рис. 5.1). Аналитическое выражение момента силы относительно точки Пусть задана сила
приложенная в точке
где
Запишем векторное произведение (5.1) с помощью определителя:
или Это есть аналитическое выражение момента силы относительно точки О.
5.2. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ Моментом силы
Рис. 5.2 Покажем на рис. 5.2 произвольно расположенную силу и ее вектор-момент относительно некоторой точки О. Если поместить в точку О декартову систему координат Oxyz, и спроецировать вектор-момент на оси этой системы, то полученные проекции по определению будут являться моментами силы относительно координатных осей. Если аналитически представить вектор-момент силы через его проекции на оси то сравнивая (5.5) с (5.3), получим аналитические выражения для моментов силы относительно координатных осей, проходящих через центр О:
5.2. ВЫЧИСЛЕНИЕ МОМЕНТА СИЛЫ ОТНОСИТЕЛЬНО ОСИ Выберем точку О, принадлежащую некоторой оси z.
Спроецируем вектора То есть для того, чтобы вычислить момент силы относительно оси z, необходимо выполнить следующие действия: 1. Спроецировать силу 2. Найти модуль момента, для чего следует умножить модуль проекции A. сила параллельна оси, B. сила пересекает ось, Главный момент системы сил относительно некоторого центра О будет равен нулю в том случае, когда все три суммы моментов исходных сил системы относительно осей, проходящих через центр О, будут равны нулю. 5.5. ЗАВИСИМОСТЬ ГЛАВНОГО МОМЕНТА ОТ ВЫБОРА ТОЧКИ ПРИВЕДЕНИЯ
Пусть задана произвольная система сил (рис. 5.5), главный момент которой относительно центра А равен
Выберем новый центр приведения − точку B, относительно которой положение старого центра A определяется радиус-вектором Определим главный момент системы сил относительно нового центра B.
Первое слагаемое представляет собой векторное произведение радиус-вектора
а второе слагаемое равно главному моменту системы относительно старого центра приведения A:
В результате получаем, что при перемене центра приведения главный момент меняется по закону
Рис.5.5 Выводы: 1. Если для некоторого центра A главный вектор системы равен нулю ( 2. Если для некоторого центра A главный момент и главный вектор системы равны нулю ( 5.6. МОМЕНТЫ СИЛ, РАСПОЛОЖЕННЫХ В ОДНОЙ ПЛОСКОСТИ Плоской системой называется система сил, линии действия которых лежат в одной плоскости. При расположении всех сил системы на одной плоскости вектора моментов сил системы относительно точек плоскости расположены к этой плоскости перпендикулярно. Для указания их направления достаточно одного знака − знака проекции вектора на ось z, перепендикулярную к плоскости.
Рис. 5.6 По этой причине при рассмотрении плоских систем под моментом силы относительно точки на самом деле понимают скалярную величину: момент силы относительно оси z, проходящей через моментную точку перпендикулярно к плоскости действия сил. То есть Величина момента равна произведению силы на плечо: Знак момента принимается соответствующим знаку проекции вектора на ось z на ось. Из рисунка видно, что проекция имеет знак «плюс», когда при взгляде на плоскость с конца оси z действие момента происходит против хода часовой стрелки (правило правого винта). Сложив моменты всех сил системы относительно точки О, получим скалярную величину – главный алгебраический момент плоской системы сил относительно точки О:
Тема 6. ТЕОРИЯ ПАР
6.1. СЛОЖЕНИЕ ДВУХ ПАРАЛЛЕЛЬНЫХ СИЛ До сих пор мы изучили лишь вопрос о сложении сходящихся сил. Перейдем теперь к определению равнодействующей системы параллельных сил, остановившись сначала на случае двух параллельных сил, приложенных в точках А и В. Здесь возможны два варианта: 1) силы направлены в одну сторону (рис. 6.1). Рис. 6.1 2) силы направлены в противоположные стороны и не равны по модулю (рис. 6.2). Для определенности пусть Рис. 6.2 В обоих случаях величину равнодействующей и положение линии ее действия можно найти с помощью следующей теоремы, которую мы приводим без доказательства: ТЕОРЕМА Равнодействующая двух параллельных сил геометрически равна их главному вектору. Линия ее действия расположена в плоскости сил, и проходит параллельно линиям действия сил. Линия действия равнодействующей делит расстояние между точками приложения сил на отрезки, которые обратно пропорциональны модулям сил. То есть: В первом случае модуль равнодействующей равен а во втором случае Линия действия равнодействующей проходит через точку С, которая в первом случае расположена в пределах отрезка АВ, а во втором случае, − за его пределами со стороны большей силы. Отрезки, определяющие положение точки С, в обоих случаях определяются с помощью пропорций:
где Следствия из теоремы: 1. Любую силу можно разложить на две параллельные силы, направленные в одну или в разные стороны. Это можно сделать бесконечным количеством способов. 2. Легко заметить, что модули моментов сил 3. Если система параллельных сил состоит более чем из двух сил, то, последовательно суммируя эти силы, можно найти ее равнодействующую (при условии, что эта равнодействующая существует).
6.2. ПАРА СИЛ, МОМЕНТ ПАРЫ В предыдущем параграфе, суммируя параллельные противоположно направленные силы, мы вводили существенное условие: При Главный вектор такой системы по модулю равен нулю. Если бы ее равнодействующая по модулю тоже была равна нулю, то система находилась бы в равновесии. Однако, эта система в равновесии не находится, что следует из аксиомы 1. Вывод: Тема 7. Любая система сил при приведении к произвольному центру заменяется одной силой и одной парой. При этом сила равна главному вектору системы сил и приложена в центре приведения, а пара имеет момент, равный главному моменту системы сил относительно центра приведения. Доказательство Рассмотрим произвольную систему сил Следуя методу Пуансо, каждую силу системы Образовавшуюся в точке О систему сходящихся сил (рис. 7.3) заменим одной силой, которая равна главному вектору системы:
Рис. 7.3 Систему присоединенных пар заменим одной парой (рис. 7.3), момент которой равен сумме моментов присоединенных пар Теорема доказана. СЛЕДСТВИЕ: Тема 8. ЧАСТНЫЕ СЛУЧАИ СИСТЕМ СИЛ В частных случаях, когда на систему сил наложены какие-либо ограничения, число необходимых уравнений равновесия может быть меньше шести, поскольку часть из них будут являться тождествами. Рассмотрим примеры. Наиболее важной с точки зрения практического применения является случай, когда все силы расположены в одной плоскости. Такие системы называют плоскими системами сил. 8.1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ Рассмотрим случай приведения к заданному центру Пусть к твердому телу приложены силы Примем за центр приведения некоторую точку Сложив сходящиеся силы, получим главный вектор системы сил Рис. 8.1
Моменты присоединенных пар равны моментам сил системы относительно центра приведения, то есть
Сложив алгебраические моменты всех сил относительно точки О, получим алгебраический главный момент системы сил относительно точки О.
Таким образом (рис. 8.1,в), Силы, произвольно расположенные на плоскости, можно привести к одной силе, приложенной в центре приведения, равной главному вектору данной системы сил, и к лежащей в той же плоскости паре сил с алгебраическим моментом, равным главному алгебраическому моменту системы сил относительно центра приведения. То есть
Выбор центра приведения не отражается на модуле и направлении главного вектора, но влияет на величину и знак главного момента.
8.2. УПРОЩЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ Итак, любая плоская система сил может быть заменена · одной силой (равной главному вектору системы сил · одной парой (с алгебраическим моментом, равным главному алгебраическому моменту системы сил относительно центра приведения Однако в ряде случаев и эту систему сил можно упростить. Рассмотрим эти случаи. 1. Если 2. Если 3. Если 4. Если
Рассмотрим последний случай подробнее (рис. 8.2). Так как элементы пары можно изменять, сохраняя при этом ее момент, расположим пару 1. пусть одна из сил пары ( 2. пусть модули сил, составляющих пару, равны модулю главного вектора: 3. Уравновешенную систему сил Исходная система сил оказывается эквивалентной одной силе 8.3. УСЛОВИЯ РАВНОВЕСИЯ ПЛОСКОЙ СИСТЕМЫ СИЛ Поскольку плоская система сил является частным случаем произвольной пространственной системы сил, для нее справедливы те же условия уравновешенности, что и для пространственной системы.
Пусть плоскость (рис. 8.1, а), в которой лежат линии действия сил системы — это плоскость Рассматривая шесть уравнений равновесия произвольной пространственной системы сил (7.4), легко видеть, что в данном случае уравнения
превращаются в тождества, так как все силы перпендикулярны оси z и лежат в одной плоскости с осями Таким образом, условия уравновешенности плоской системы сил в аналитической форме будут представлены только тремя уравнениями:
Последнее уравнение для плоской системы сил принято записывать иначе. Вместо того чтобы говорить о «моментах сил относительно оси
Тогда уравнения равновесия для плоской системы сил принимают вид:
Это есть первая (основная) форма уравнений равновесия произвольной плоской системы сил. Она состоит из двух уравнений проекций сил на две проведенные произвольным образом перпендикулярные оси х и у и одного уравнения моментов сил относительно произвольной точки О плоскости ху. Можно показать, что системе уравнений (8.1) равносильны еще две формы записей уравнений равновесия для плоской системы сил.
Это вторая форма уравнений равновесия плоской системы сил. Она содержит одно уравнение проекций сил на какую-либо ось
Это третья форма уравнений равновесия плоской системы сил. Она содержит три уравнения моментов сил относительно трех произвольных точек А, В и С. При этом точки А, В и С не должны лежать на одной прямой. Из трех возможных вариантов следует выбирать ту форму записи уравнений равновесия, с помощью которой данная конкретная задача будет решаться наиболее рациональным образом.
8.4. ДРУГИЕ ЧАСТНЫЕ СЛУЧАИ УСЛОВИЙ РАВНОВЕСИЯ Сходящиеся системы сил Если линии действия всех сил системы проходят через одну точку, то моменты сил относительно этой точки (или любой проходящей через нее оси) будут равны нулю. В этом случае уравнен
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.81.206 (0.29 с.) |
 Диевский В.А. Теоретическая механика: Учебное пособие.—СПб.: «Лань», 2005.
Диевский В.А. Теоретическая механика: Учебное пособие.—СПб.: «Лань», 2005. .
.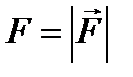 .
.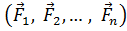 .
. .
. .
. .
.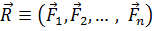 .
. , но при этом
, но при этом 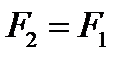 .
.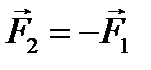 и
и  .
. в системе имеется и сила противодействия
в системе имеется и сила противодействия 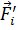 , а их векторная сумма равна нулю:
, а их векторная сумма равна нулю: 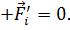
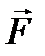 , которая представлена вектором с началом в точке
, которая представлена вектором с началом в точке 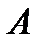 и с концом в точке
и с концом в точке 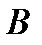 (рис. 3.4).
(рис. 3.4).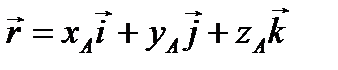 ,
,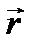 на координатные оси равны координатам точки
на координатные оси равны координатам точки  , в которой приложена сила
, в которой приложена сила 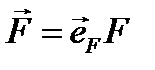 ,
,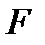 − модуль силы, а
− модуль силы, а 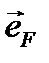 − единичный вектор, указывающий направление силы (направляющий вектор):
− единичный вектор, указывающий направление силы (направляющий вектор): 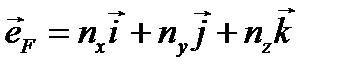 ,
,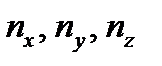 − направляющие косинусы вектора (рис. 3.4):
− направляющие косинусы вектора (рис. 3.4):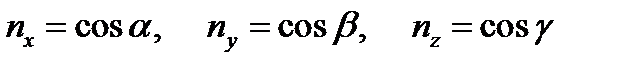 .
.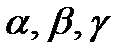 и значение его модуля −
и значение его модуля − 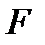 .
.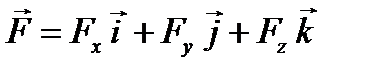 .
.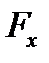 ,
, 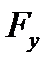 ,
, 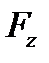 − проекции вектора
− проекции вектора 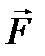 на координатные оси (рис. 3.4).
на координатные оси (рис. 3.4).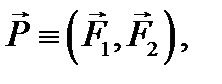
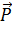 и
и 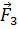 , линия действия которой также пройдет через точку О:
, линия действия которой также пройдет через точку О: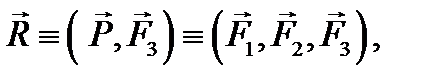
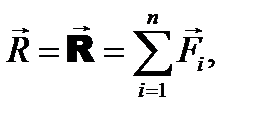 (4.1)
(4.1)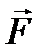 относительно некоторой точки О называется величина
относительно некоторой точки О называется величина 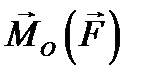 , равная векторному произведению радиус-вектора, проведенного из данной точки в точку приложения силы, на саму эту силу:
, равная векторному произведению радиус-вектора, проведенного из данной точки в точку приложения силы, на саму эту силу: . (5.1)
. (5.1)
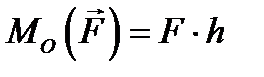 . (5.2)
. (5.2) 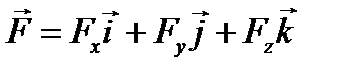 ,
, , положение которой указано радиус-вектором
, положение которой указано радиус-вектором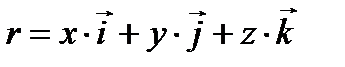 ,
, − орты декартовых координатных осей,
− орты декартовых координатных осей, − проекции радиус-вектора,
− проекции радиус-вектора,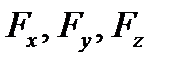 − проекции силы на координатные оси.
− проекции силы на координатные оси. ,
,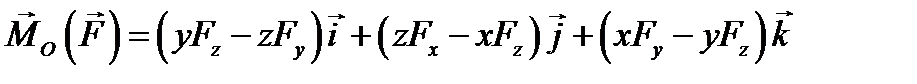 (5.3)
(5.3) относительно некоторой оси
относительно некоторой оси 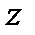 называется скалярная величина
называется скалярная величина  , равная проекции (рис. 5.2) на эту ось момента силы, вычисленного относительно какой-либо точки О этой оси:
, равная проекции (рис. 5.2) на эту ось момента силы, вычисленного относительно какой-либо точки О этой оси: (5.4)
(5.4)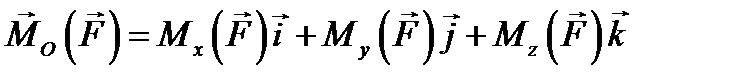 , (5.5)
, (5.5) (5.6)
(5.6)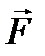 и
и 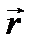 на плоскость П, которая перпендикулярна оси z. Проекции обозначим
на плоскость П, которая перпендикулярна оси z. Проекции обозначим 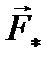 и
и 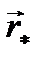 . Проекции этих векторов на ось z равны нулю. С помощью приведенных выше формул (5.5) и (5.6) можно убедиться в том, что величина момента силы
. Проекции этих векторов на ось z равны нулю. С помощью приведенных выше формул (5.5) и (5.6) можно убедиться в том, что величина момента силы  на плоскость, перпендикулярную оси.
на плоскость, перпендикулярную оси.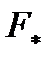 на ее плечо
на ее плечо 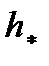 .
.
 , а положение некоторой
, а положение некоторой 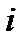 -й силы системы − радиус-вектором
-й силы системы − радиус-вектором  , который равен
, который равен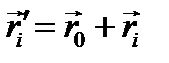

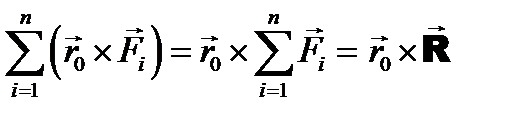 ,
,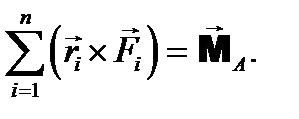
 (5.14)
(5.14)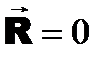 ), то главный момент для всех точек пространства будет одинаков, поскольку
), то главный момент для всех точек пространства будет одинаков, поскольку  в соответствии с формулой (5.14).
в соответствии с формулой (5.14).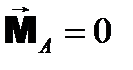 и
и 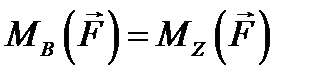
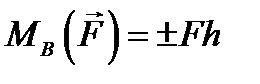 .
.
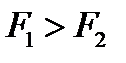
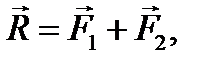
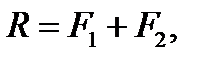
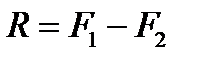 , причем равнодействующая направлена в сторону большей силы.
, причем равнодействующая направлена в сторону большей силы.
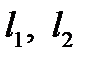 − расстояния от линии действия равнодействующей
− расстояния от линии действия равнодействующей 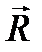 до линий действия сил
до линий действия сил  и
и 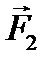 соответственно, а
соответственно, а 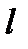 − расстояние между линиями действия сил
− расстояние между линиями действия сил 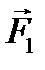 и
и  относительно точки С одинаковы, а сумма моментов будет равна нулю:
относительно точки С одинаковы, а сумма моментов будет равна нулю: 
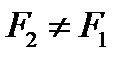 .
.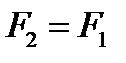 ,
, 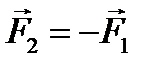 имеет место особый случай.
имеет место особый случай.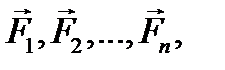 (рис. 7.2., а).
(рис. 7.2., а).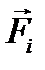 приведем к центру О, добавляя (рис. 7.2, б) при каждом переносе присоединенную пару с моментом
приведем к центру О, добавляя (рис. 7.2, б) при каждом переносе присоединенную пару с моментом 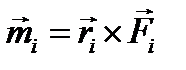 , который равен моменту данной силы относительно точки О:
, который равен моменту данной силы относительно точки О:
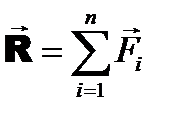 (7.1)
(7.1)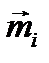 и следовательно, равен главному моменту системы сил:
и следовательно, равен главному моменту системы сил: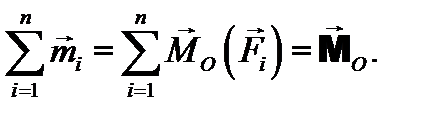 (7.2)
(7.2) сил, произвольно расположенных на плоскости.
сил, произвольно расположенных на плоскости.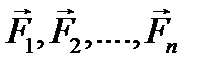 , лежащие в одной плоскости и приложенные соответственно в точках
, лежащие в одной плоскости и приложенные соответственно в точках  (рис. 8.1,а).
(рис. 8.1,а). , лежащую в этой плоскости и приведем все силы к этому центру. В результате приведения получим систему сходящихся сил
, лежащую в этой плоскости и приведем все силы к этому центру. В результате приведения получим систему сходящихся сил 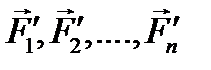 , приложенных в центре
, приложенных в центре  и лежащих в одной плоскости, а также систему присоединенных пар, алгебраические моменты которых равны
и лежащих в одной плоскости, а также систему присоединенных пар, алгебраические моменты которых равны  (рис. 8.1,б).
(рис. 8.1,б).  , который будет лежать в той же плоскости, что и вся система.
, который будет лежать в той же плоскости, что и вся система.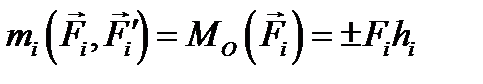
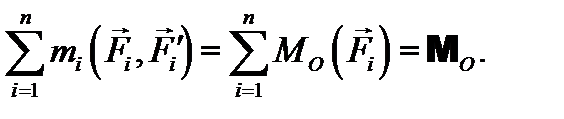
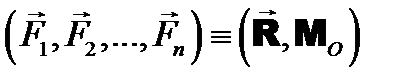 .
. и приложенной в центре приведения О) и/или
и приложенной в центре приведения О) и/или ).
). и
и 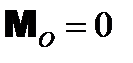 , то система сил уравновешена (эквивалентна нулю), дальнейшее упрощение ее невозможно.
, то система сил уравновешена (эквивалентна нулю), дальнейшее упрощение ее невозможно. , то система сил эквивалентна одной паре сил, дальнейшее упрощение ее невозможно.
, то система сил эквивалентна одной паре сил, дальнейшее упрощение ее невозможно. и
и  , то система сил эквивалентна одной силе, то есть имеет равнодействующую, которая проходит через центр приведения О, Дальнейшее упрощение системы невозможно.
, то система сил эквивалентна одной силе, то есть имеет равнодействующую, которая проходит через центр приведения О, Дальнейшее упрощение системы невозможно. и
и 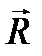 , т. е. имеет равнодействующую равную главному вектору, которая не проходит через центр приведения О.
, т. е. имеет равнодействующую равную главному вектору, которая не проходит через центр приведения О.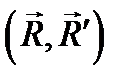 , момент которой равен главному моменту системы сил
, момент которой равен главному моменту системы сил 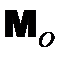 следующим образом:
следующим образом: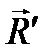 ) будет приложена в точке О и направлена против силы
) будет приложена в точке О и направлена против силы  (рис. 8.2, б);
(рис. 8.2, б); 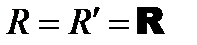 , и тогда плечо пары будет равно
, и тогда плечо пары будет равно 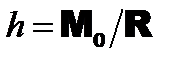 .
.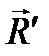 и
и  можно исключить.
можно исключить.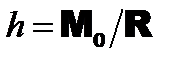 от центра О.
от центра О. (7.4)
(7.4)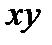 . Ось
. Ось 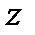 перпендикулярна этой плоскости.
перпендикулярна этой плоскости.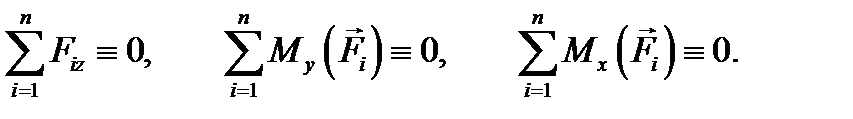
 и
и 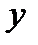 .
.
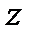 , проходящей через некоторую точку О, говорят о «моментах сил относительно точки О» (см. § 5.6) и записывают последнее уравнение в виде:
, проходящей через некоторую точку О, говорят о «моментах сил относительно точки О» (см. § 5.6) и записывают последнее уравнение в виде: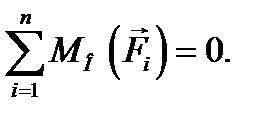
 (8.1)
(8.1)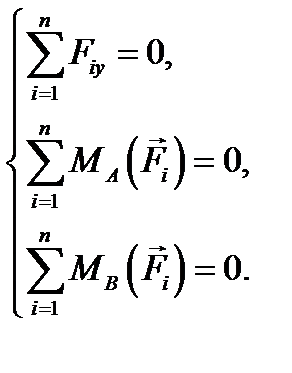 (8.2)
(8.2) и два уравнения моментов сил относительно точек А и В (ось
и два уравнения моментов сил относительно точек А и В (ось 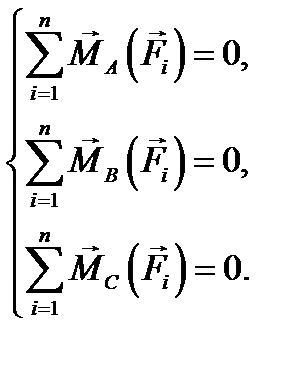 (8.3)
(8.3)


