
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекции силы, операции с силамиСодержание книги
Поиск на нашем сайте
3.1. ПРОЕКЦИИ СИЛЫ Проекцией вектора на ось называется скалярная величина, равная произведению модуля вектора на косинус угла между направлением силы и положительным направлением оси. То есть проекция Дадим этому определению геометрическое пояснение. Пусть в трехмерном пространстве задана ось L, направление которой указано вектором единичной длины Через точки А и В проведем перпендикулярно оси L две плоскости: П1 и П2. Параллельно оси L через точку А проведем направление n. Численно величина проекции вектора на ось равна отрезку АС или отрезку А1С1, а знак проекции зависит от величины угла: · при · при · при
Можно дать и другое определение проекции вектора на ось. Проекцией вектора на ось называется скалярное произведение вектора на направляющий вектор оси. Действительно, где
Рис. 3.1 Рассмотрим некоторые частные случаи проецирования вектора на ось: Рис. 3.2 Проекцией вектора на плоскость называется вектор, заключенный между проекциями начала и конца вектора на эту плоскость. Так на рис. 3.3 вектор Если вектор задан выражением
то аналитическое выражение проекции этого вектора на плоскость Oxy можно получить, приравняв к нулю проекцию вектора на ось z:
Рис. 3.3 Модуль этого вектора равен: Для определения проекции силы на ось удобно сначала спроецировать силу на плоскость, в которой эта ось лежит, а затем найденную проекцию спроецировать на ось. Этот прием называют методом двойного проецирования. Аналогично проецируется сила и на две другие плоскости. Заметим, что · Проекции вектора на параллельные оси равны. · Проекции вектора на параллельные плоскости геометрически равны.
3.2. СПОСОБЫ ЗАДАНИЯ СИЛЫ Рассмотрим силу
Для указания точки приложения силы используем радиус-вектор
соединяющий начало системы координат и точку приложения силы. Проекции вектора Информация о величине и направлении силы Рис. 3.4 Первый способ Представим вектор силы в виде произведения (рис. 3.4) где
где
Чтобы таким способом задать вектор, необходимо знать углы Второй способ (аналитический) Аналитическое выражение вектора силы дается следующим образом: где То есть, для аналитического задания вектора силы необходимо указать три его проекции:
|
|||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.177.252 (0.009 с.) |

 вектора
вектора 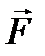 на ось
на ось 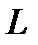 равна
равна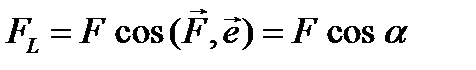 .
.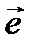 (направляющим вектором), и вектор
(направляющим вектором), и вектор 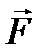 , начало которого находится в т. А, а конец, ─ в т. В (рис. 3.1).
, начало которого находится в т. А, а конец, ─ в т. В (рис. 3.1).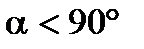 проекция силы положительна,
проекция силы положительна,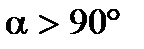 ─ отрицательна,
─ отрицательна,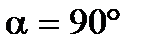 ─ равна нулю.
─ равна нулю.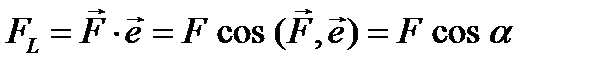 ,
,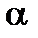 ─ угол между направлением вектора
─ угол между направлением вектора 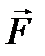 и единичного вектора
и единичного вектора 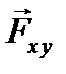 является проекцией вектора
является проекцией вектора 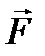 на плокость Oxy.
на плокость Oxy.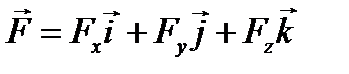 ,
,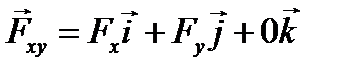 .
.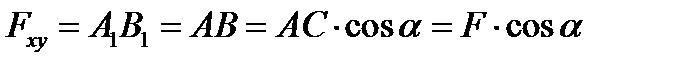
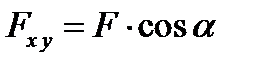
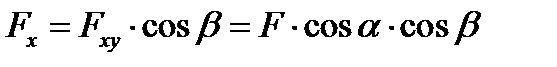
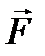 , которая представлена вектором с началом в точке
, которая представлена вектором с началом в точке 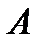 и с концом в точке
и с концом в точке 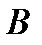 (рис. 3.4).
(рис. 3.4).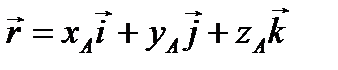 ,
,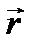 на координатные оси равны координатам точки
на координатные оси равны координатам точки  , в которой приложена сила
, в которой приложена сила 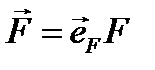 ,
,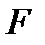 − модуль силы, а
− модуль силы, а 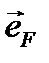 − единичный вектор, указывающий направление силы (направляющий вектор):
− единичный вектор, указывающий направление силы (направляющий вектор): 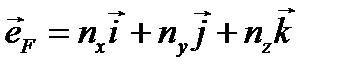 ,
,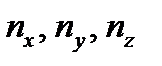 − направляющие косинусы вектора (рис. 3.4):
− направляющие косинусы вектора (рис. 3.4):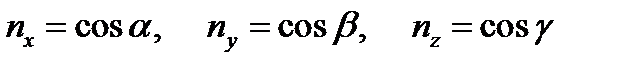 .
.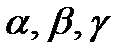 и значение его модуля −
и значение его модуля − 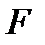 .
.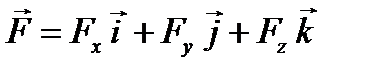 .
.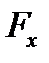 ,
, 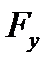 ,
, 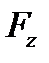 − проекции вектора
− проекции вектора 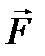 на координатные оси (рис. 3.4).
на координатные оси (рис. 3.4).


