
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
геометрическое место точек, для которых главный вектор и главный момент системы сил коллинеарны, называется главной осью системы сил.⇐ ПредыдущаяСтр 11 из 11
Рассмотрим случай, когда к материальному телу приложена сила и пара сил таким образом, что линия действия силы расположена перпендикулярно плоскости действия сил пары. Рис. 7.6
Эта система сил не может быть более упрощена. Такая система сил называется динамическим винтом, силовым винтом или динамой.
Тема 8. ЧАСТНЫЕ СЛУЧАИ СИСТЕМ СИЛ В частных случаях, когда на систему сил наложены какие-либо ограничения, число необходимых уравнений равновесия может быть меньше шести, поскольку часть из них будут являться тождествами. Рассмотрим примеры. Наиболее важной с точки зрения практического применения является случай, когда все силы расположены в одной плоскости. Такие системы называют плоскими системами сил. 8.1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ Рассмотрим случай приведения к заданному центру Пусть к твердому телу приложены силы Примем за центр приведения некоторую точку Сложив сходящиеся силы, получим главный вектор системы сил Рис. 8.1
Моменты присоединенных пар равны моментам сил системы относительно центра приведения, то есть
Сложив алгебраические моменты всех сил относительно точки О, получим алгебраический главный момент системы сил относительно точки О.
Таким образом (рис. 8.1,в), Силы, произвольно расположенные на плоскости, можно привести к одной силе, приложенной в центре приведения, равной главному вектору данной системы сил, и к лежащей в той же плоскости паре сил с алгебраическим моментом, равным главному алгебраическому моменту системы сил относительно центра приведения. То есть
Выбор центра приведения не отражается на модуле и направлении главного вектора, но влияет на величину и знак главного момента.
8.2. УПРОЩЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
Итак, любая плоская система сил может быть заменена · одной силой (равной главному вектору системы сил · одной парой (с алгебраическим моментом, равным главному алгебраическому моменту системы сил относительно центра приведения Однако в ряде случаев и эту систему сил можно упростить. Рассмотрим эти случаи. 1. Если 2. Если 3. Если 4. Если
Рассмотрим последний случай подробнее (рис. 8.2). Так как элементы пары можно изменять, сохраняя при этом ее момент, расположим пару 1. пусть одна из сил пары ( 2. пусть модули сил, составляющих пару, равны модулю главного вектора: 3. Уравновешенную систему сил Исходная система сил оказывается эквивалентной одной силе 8.3. УСЛОВИЯ РАВНОВЕСИЯ ПЛОСКОЙ СИСТЕМЫ СИЛ Поскольку плоская система сил является частным случаем произвольной пространственной системы сил, для нее справедливы те же условия уравновешенности, что и для пространственной системы.
Пусть плоскость (рис. 8.1, а), в которой лежат линии действия сил системы — это плоскость Рассматривая шесть уравнений равновесия произвольной пространственной системы сил (7.4), легко видеть, что в данном случае уравнения
превращаются в тождества, так как все силы перпендикулярны оси z и лежат в одной плоскости с осями Таким образом, условия уравновешенности плоской системы сил в аналитической форме будут представлены только тремя уравнениями:
Последнее уравнение для плоской системы сил принято записывать иначе. Вместо того чтобы говорить о «моментах сил относительно оси
Тогда уравнения равновесия для плоской системы сил принимают вид:
Это есть первая (основная) форма уравнений равновесия произвольной плоской системы сил. Она состоит из двух уравнений проекций сил на две проведенные произвольным образом перпендикулярные оси х и у и одного уравнения моментов сил относительно произвольной точки О плоскости ху. Можно показать, что системе уравнений (8.1) равносильны еще две формы записей уравнений равновесия для плоской системы сил.
Это вторая форма уравнений равновесия плоской системы сил. Она содержит одно уравнение проекций сил на какую-либо ось
Это третья форма уравнений равновесия плоской системы сил. Она содержит три уравнения моментов сил относительно трех произвольных точек А, В и С. При этом точки А, В и С не должны лежать на одной прямой. Из трех возможных вариантов следует выбирать ту форму записи уравнений равновесия, с помощью которой данная конкретная задача будет решаться наиболее рациональным образом.
8.4. ДРУГИЕ ЧАСТНЫЕ СЛУЧАИ УСЛОВИЙ РАВНОВЕСИЯ Сходящиеся системы сил Если линии действия всех сил системы проходят через одну точку, то моменты сил относительно этой точки (или любой проходящей через нее оси) будут равны нулю. В этом случае уравнения моментов (7.4, г,д,е) оказываются тождествами (т. е. выполняются автоматически); тогда для системы сходящихся сил остаются только уравнения проекций сил:
Если при этом все силы системы лежат в одной плоскости Oxy, то и уравнение (в) также обратится в тождество и в системе останется два уравнения: Системы пар сил Если система сил состоит только из пар, для каждой из которых, как известно, сумма векторов сил равна нулю, то уравнения проекций сил (а,б,в) в (7.4) оказываются тождествами. Тогда для системы пар остаются только уравнения сумм проекций моментов пар, которые были записаны нами как уравнения (6.7): Если при этом все силы системы лежат в одной плоскости, то равновесие системы описывается одним уравнением:
Системы параллельных сил Пусть линии действия всех сил параллельны друг другу (рис. 8.3). Направим ось z параллельно этим силам. В этом случае являются тождествами уравнения проекций сил на оси х и у, а также уравнения моментов сил относительно оси z, то есть уравнения (а,б,е) из (7.4).
Тогда остаются три уравнения: Рис. 8.3 которые называются уравнениями равновесия пространственной системы параллельных сил. Тема 9. ЦЕНТР ТЯЖЕСТИ
9.1. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ Рассмотрим систему (рис. 9.1) параллельных и одинаково направленных сил Очевидно, что эта система сил имеет равнодействующую которая имеет то же направление, что и силы системы:
По модулю она равна Пусть единичный вектор
Изменим направление сил системы. Для этого с помощью единичного вектора Тогда все силы системы повернутся на один и тот же угол α и образуется новая система параллельных сил
которая отличается направлением, но имеет тот же модуль. Такая операция называется поворотом системы параллельных сил. Покажем, что имеется такая точка Согласно теореме Вариньона, момент равнодействующей системы сил относительно любой точки равен сумме моментов всех сил системы относительно этой точки. В рассматриваемом случае, например,
где Выразим в последнем равенстве все векторы сил через единичный вектор, после чго оно примет вид:
Чтобы это равенство выполнялось при любом по направлению единичном векторе
откуда получаем: Точка С, через которую линия действия равнодействующей пройдет при любом повороте системы параллельных сил, называется центром параллельных сил. Формула (9.1) определяет положение центра параллельных сил через его радиус-вектор. Координаты центра параллельных сил можно получить, если спроектировать равенство (9.1) на координатные оси:
Рис. 9.1
Заметим, что формулы (9.1) и (9.2) справедливы и для случая параллельных сил, направленных в разные стороны, если в них полагать величины
9.2. ЦЕНТР ТЯЖЕСТИ Силы притяжения отдельных частиц тела к Земле направлены к центру Земли. Поскольку размеры рассматриваемых тел малы по сравнению с радиусом Земли, эти силы можно считать параллельными. Равнодействующая этих параллельных сил — это сила тяжести (ее модуль — это вес тела), а центр этой системы параллельных сил (в котором всегда приложена сила тяжести) называется центром тяжести тела. Поворот тела относительно Земли приводит к повороту системы сил относительно самого тела. При этом положение центра тяжести тела не зависит от расположения тела в пространстве. Если обозначить модули сил тяжести отдельных частей тела
из которой следует, что
Если тело однородное, т. е. все его части имеют один и тот же удельный вес После подстановки этих выражений в формулы (9.4) и сокращения мы получаем соотношения для координат центра тяжести объема:
Центр тяжести однородной тонкой пластины постоянной толщины (оболочки) — может быть вычислен аналогично через площади отдельных ее частей
Если при этом вся пластина лежит в одной плоскости, например в плоскости Oxy), то третье уравнение в (9.6) обращается в тождество и центр тяжести определяется по формулам
Центр тяжести однородного пространственного ломаного стержня, состоящего из ряда прямолинейных участков, определяется через длины его участков
|
||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.121.131 (0.05 с.) |
 сил, произвольно расположенных на плоскости.
сил, произвольно расположенных на плоскости.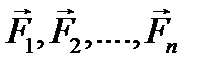 , лежащие в одной плоскости и приложенные соответственно в точках
, лежащие в одной плоскости и приложенные соответственно в точках  (рис. 8.1,а).
(рис. 8.1,а). , лежащую в этой плоскости и приведем все силы к этому центру. В результате приведения получим систему сходящихся сил
, лежащую в этой плоскости и приведем все силы к этому центру. В результате приведения получим систему сходящихся сил 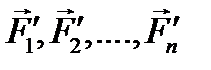 , приложенных в центре
, приложенных в центре  и лежащих в одной плоскости, а также систему присоединенных пар, алгебраические моменты которых равны
и лежащих в одной плоскости, а также систему присоединенных пар, алгебраические моменты которых равны  (рис. 8.1,б).
(рис. 8.1,б).  , который будет лежать в той же плоскости, что и вся система.
, который будет лежать в той же плоскости, что и вся система.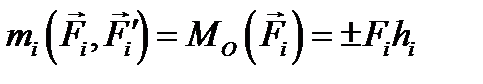
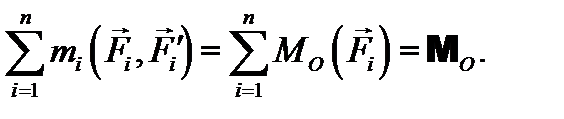
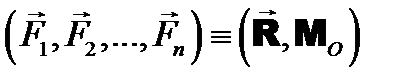 .
. и приложенной в центре приведения О) и/или
и приложенной в центре приведения О) и/или ).
). и
и 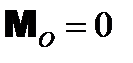 , то система сил уравновешена (эквивалентна нулю), дальнейшее упрощение ее невозможно.
, то система сил уравновешена (эквивалентна нулю), дальнейшее упрощение ее невозможно. , то система сил эквивалентна одной паре сил, дальнейшее упрощение ее невозможно.
, то система сил эквивалентна одной паре сил, дальнейшее упрощение ее невозможно. и
и  , то система сил эквивалентна одной силе, то есть имеет равнодействующую, которая проходит через центр приведения О, Дальнейшее упрощение системы невозможно.
, то система сил эквивалентна одной силе, то есть имеет равнодействующую, которая проходит через центр приведения О, Дальнейшее упрощение системы невозможно. и
и 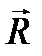 , т. е. имеет равнодействующую равную главному вектору, которая не проходит через центр приведения О.
, т. е. имеет равнодействующую равную главному вектору, которая не проходит через центр приведения О.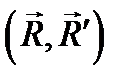 , момент которой равен главному моменту системы сил
, момент которой равен главному моменту системы сил 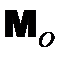 следующим образом:
следующим образом: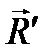 ) будет приложена в точке О и направлена против силы
) будет приложена в точке О и направлена против силы  (рис. 8.2, б);
(рис. 8.2, б); 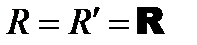 , и тогда плечо пары будет равно
, и тогда плечо пары будет равно 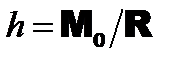 .
.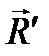 и
и  можно исключить.
можно исключить.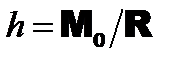 от центра О.
от центра О. (7.4)
(7.4) . Ось
. Ось  перпендикулярна этой плоскости.
перпендикулярна этой плоскости.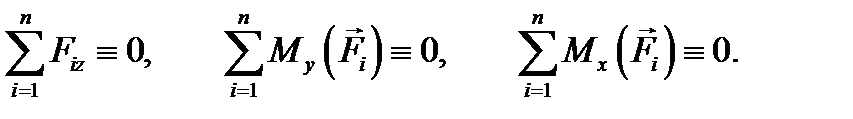
 и
и 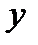 .
.
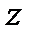 , проходящей через некоторую точку О, говорят о «моментах сил относительно точки О» (см. § 5.6) и записывают последнее уравнение в виде:
, проходящей через некоторую точку О, говорят о «моментах сил относительно точки О» (см. § 5.6) и записывают последнее уравнение в виде: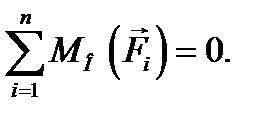
 (8.1)
(8.1)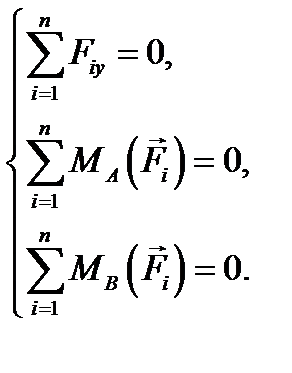 (8.2)
(8.2) и два уравнения моментов сил относительно точек А и В (ось
и два уравнения моментов сил относительно точек А и В (ось 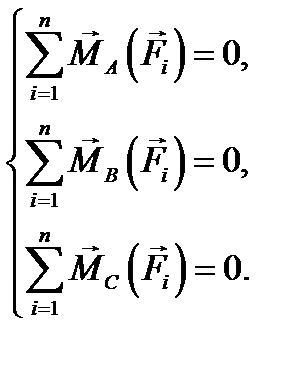 (8.3)
(8.3) (4.2)
(4.2)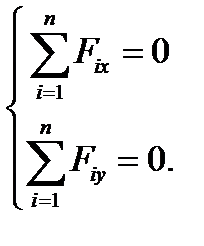 (4.3)
(4.3)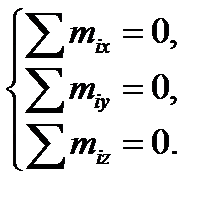 (6.5)
(6.5)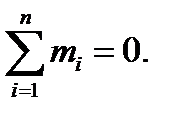 (6.7)
(6.7)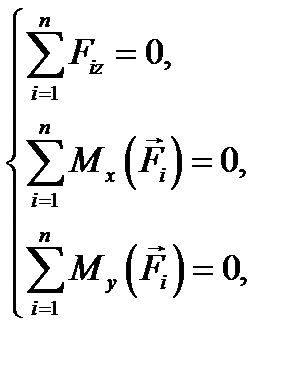 (8.4)
(8.4) приложенных к твердому телу в точках
приложенных к твердому телу в точках 


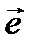 указывает направление сил системы. Тогда силы можно записать в виде
указывает направление сил системы. Тогда силы можно записать в виде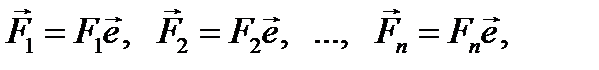
 .
.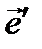 укажем новое направление (рис. 9.1).
укажем новое направление (рис. 9.1). с теми же модулями, которая имеет равнодействующую,
с теми же модулями, которая имеет равнодействующую, 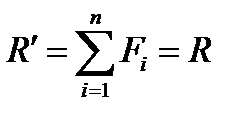 ,
, , через которую линия действия равнодействующей пройдет при любом направлении сил системы.
, через которую линия действия равнодействующей пройдет при любом направлении сил системы. или
или 
 — радиус-векторы точек
— радиус-векторы точек 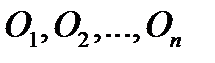 , проведенные из начала координат (точки
, проведенные из начала координат (точки  ),
), 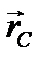 — радиус-вектор точки С.
— радиус-вектор точки С. или
или 
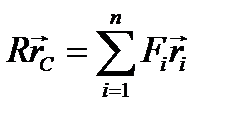
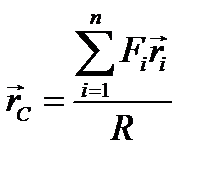 (9.1)
(9.1) (9.2)
(9.2)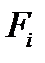 для сил одного направления со знаком «плюс», а для сил другого направления со знаком «минус».
для сил одного направления со знаком «плюс», а для сил другого направления со знаком «минус».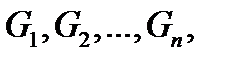 и вес тела
и вес тела  , то радиус-вектор и координаты центра тяжести могут быть вычислены по общей формуле
, то радиус-вектор и координаты центра тяжести могут быть вычислены по общей формуле , (9.3)
, (9.3)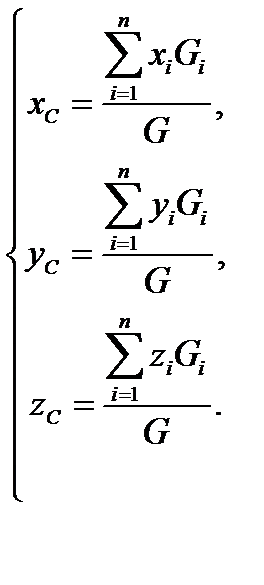 (9.4)
(9.4) , где
, где 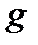 − ускорение свободного падения, а
− ускорение свободного падения, а 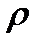 − плотность, то
− плотность, то 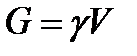 и
и 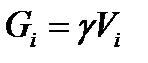 , где
, где  − объем всего тела, а
− объем всего тела, а 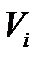 − объем
− объем 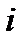 - ой его части.
- ой его части.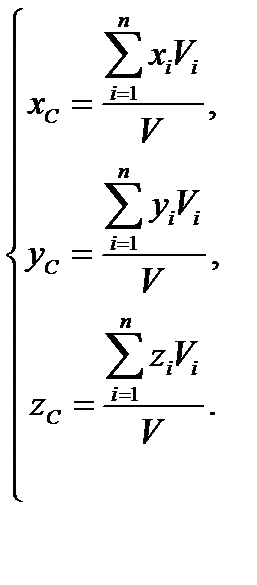 (9.5)
(9.5)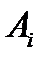 и общую площадь
и общую площадь 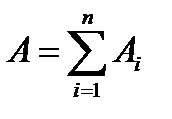 :
: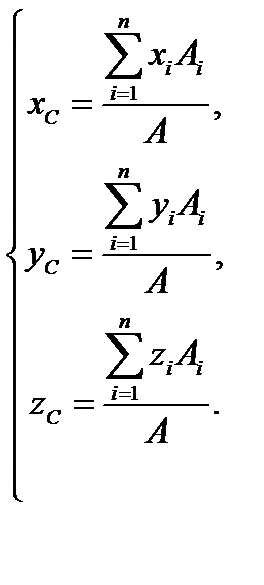 (9.6)
(9.6)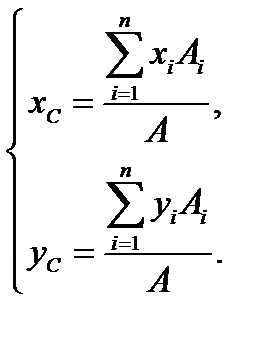 (9.7)
(9.7)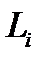 и общую длину
и общую длину 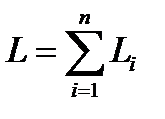 :
: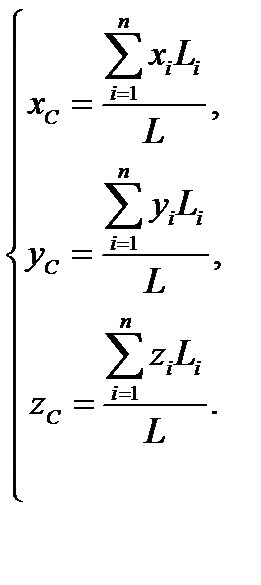 (9.8)
(9.8)


