
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если для какой-то системы сил равнодействующая существует, то она геометрически всегда равна главному вектору.
Отсюда следует, что проекции равнодействующей сходящейся системы сил определяются так же, как и проекции главного вектора::
Модуль равнодействующей равен:
а ее направляющие косинусы определяются по формулам:
4.2. УСЛОВИЯ УРАВНОВЕШЕННОСТИ СХОДЯЩЕЙСЯ СИСТЕМЫ СИЛ Система сходящихся сил эквивалентна одной силе, которая по определению является равнодействующей: В общем случае сходящаяся система не является уравновешенной. Исключение составляет случай, когда равнодействующая, а следовательно и главный вектор этой системы сил равны нулю. Равнодействующая сходящейся системы геометрически равна ее главному вектору Отсюда следует Вывод: Для равновесия системы сходящихся сил, необходимо и достаточно, чтобы выполнялись следующие условия: 1. В векторной форме: Главный вектор системы сил должен быть равен нулю,
2. В геометрической форме: Силовой многоугольник должен быть замкнут. 3. В аналитической форме: Сумма проекций сил на каждую из координатных осей должна быть равна нулю. Для системы сходящихся сил в пространстве получаем три уравнения равновесия:
где в формулах подразумевается суммирование по всем действующим силам, а для системы сходящихся сил, расположенных в одной плоскости (например, в плоскости ху), только два уравнения равновесия: поскольку третье уравнение будет выполняться автоматически.
4.3. ТЕОРЕМА О ТРЕХ СИЛАХ При решении задач иногда удобно пользоваться следующей теоремой: ТЕОРЕМА Для равновесия твердого тела, находящегося под действием трех непараллельных сил, необходимо, чтобы эти силы лежали в одной плоскости и линии их действия пересекались в одной точке. Доказательство · Пусть на тело действуют (рис. 4.4) три силы · Перенесем силы
Все три силы при этом будут лежать в одной плоскости. · Тогда на тело будут действовать только две силы: Под действием двух сил по I-й аксиоме тело может находиться в равновесии только тогда, когда силы Рис. 4.4 Примечание Теорема о трех силах дает только необходимое условие равновесия, без которого равновесие в принципе невозможно. Достаточным условием является замкнутость силового треугольника. Тема 5. МОМЕНТЫ СИЛЫ
5.1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ Величина и направление силы характеризуют действие силы в том случае, если она придает какому-либо телу поступательное движение. Вращательный эффект силы по отношению к некоторой точке или оси учитывает другая характеристика — момент силы. Моментом силы
Рис. 5.1 Направление и модуль момента силы определяются по обычному правилу векторного произведения. Направление момента силы Вектор-момент силы Модуль момента силы Модуль векторного произведения:
или Модуль момента силы относительно точки равен произведению модуля силы на ее плечо. Плечом силы называется кратчайшее (длина перпендикуляра) расстояние от точки до линии действия силы. Единица измерения модуля момента силы [M] = Нм. Из формулы (5.2) следует, что 1. момент силы относительно точки равен нулю только в том случае, когда ее плечо равно нулю, т. е. когда линия действия силы проходит через эту точку;
2. момент силы не зависит от того, где взята точка приложения силы на линии ее действия; 3. модуль момента силы равен удвоенной площади треугольника, для которого сила является основанием, а плечо высотой (рис. 5.1). Аналитическое выражение момента силы относительно точки Пусть задана сила
приложенная в точке
где
Запишем векторное произведение (5.1) с помощью определителя:
или Это есть аналитическое выражение момента силы относительно точки О.
5.2. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ Моментом силы
Рис. 5.2 Покажем на рис. 5.2 произвольно расположенную силу и ее вектор-момент относительно некоторой точки О. Если поместить в точку О декартову систему координат Oxyz, и спроецировать вектор-момент на оси этой системы, то полученные проекции по определению будут являться моментами силы относительно координатных осей. Если аналитически представить вектор-момент силы через его проекции на оси то сравнивая (5.5) с (5.3), получим аналитические выражения для моментов силы относительно координатных осей, проходящих через центр О:
5.2. ВЫЧИСЛЕНИЕ МОМЕНТА СИЛЫ ОТНОСИТЕЛЬНО ОСИ Выберем точку О, принадлежащую некоторой оси z. Спроецируем вектора То есть для того, чтобы вычислить момент силы относительно оси z, необходимо выполнить следующие действия: 1. Спроецировать силу 2. Найти модуль момента, для чего следует умножить модуль проекции
|
||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.199.243 (0.018 с.) |
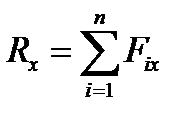
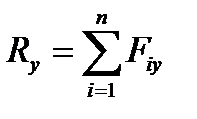
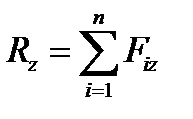 . (4.2)
. (4.2) , (4.3)
, (4.3)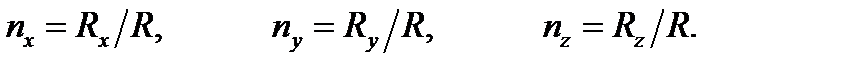 (4.4)
(4.4)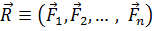 .
.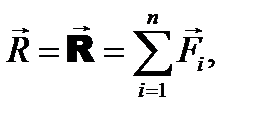 который приложен в точке схода системы.
который приложен в точке схода системы.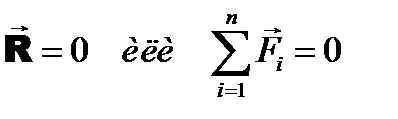 (4.5)
(4.5) , (4.6)
, (4.6)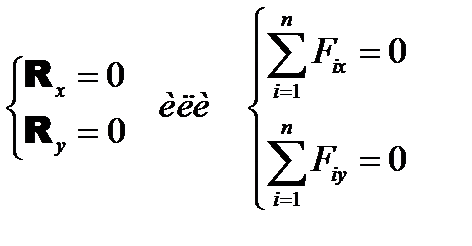 , (4.7)
, (4.7)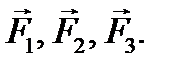
 в точку пересечения линий действия и заменим их равнодействующей, применяя аксиому параллелограмма:
в точку пересечения линий действия и заменим их равнодействующей, применяя аксиому параллелограмма: 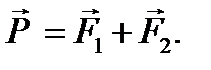
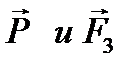 .
.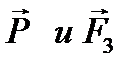 равны по величине, противоположно направлены и лежат на одной прямой. Это возможно только в том случае, когда три исходные силы лежат в одной плоскости и их линии действия пересекаются в одной точке.
равны по величине, противоположно направлены и лежат на одной прямой. Это возможно только в том случае, когда три исходные силы лежат в одной плоскости и их линии действия пересекаются в одной точке.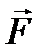 относительно некоторой точки О называется величина
относительно некоторой точки О называется величина 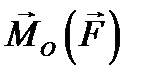 , равная векторному произведению радиус-вектора, проведенного из данной точки в точку приложения силы, на саму эту силу:
, равная векторному произведению радиус-вектора, проведенного из данной точки в точку приложения силы, на саму эту силу: . (5.1)
. (5.1)
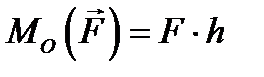 . (5.2)
. (5.2) 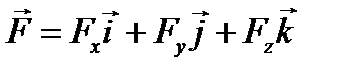 ,
, , положение которой указано радиус-вектором
, положение которой указано радиус-вектором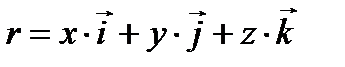 ,
, − орты декартовых координатных осей,
− орты декартовых координатных осей, − проекции радиус-вектора,
− проекции радиус-вектора,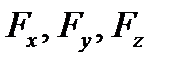 − проекции силы на координатные оси.
− проекции силы на координатные оси. ,
,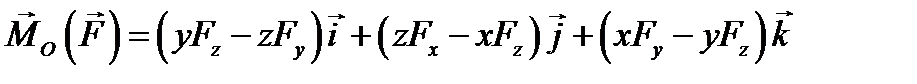 (5.3)
(5.3) относительно некоторой оси
относительно некоторой оси 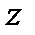 называется скалярная величина
называется скалярная величина  , равная проекции (рис. 5.2) на эту ось момента силы, вычисленного относительно какой-либо точки О этой оси:
, равная проекции (рис. 5.2) на эту ось момента силы, вычисленного относительно какой-либо точки О этой оси: (5.4)
(5.4)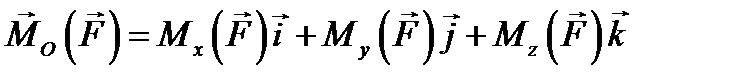 , (5.5)
, (5.5) (5.6)
(5.6)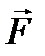 и
и 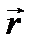 на плоскость П, которая перпендикулярна оси z. Проекции обозначим
на плоскость П, которая перпендикулярна оси z. Проекции обозначим 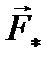 и
и 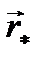 . Проекции этих векторов на ось z равны нулю. С помощью приведенных выше формул (5.5) и (5.6) можно убедиться в том, что величина момента силы
. Проекции этих векторов на ось z равны нулю. С помощью приведенных выше формул (5.5) и (5.6) можно убедиться в том, что величина момента силы  на плоскость, перпендикулярную оси.
на плоскость, перпендикулярную оси.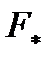 на ее плечо
на ее плечо 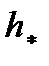 .
.


