
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Главный вектор системы сил будет равен нулю в том случае, когда все три суммы проекций исходных сил будут равны нулю.Содержание книги
Поиск на нашем сайте
3.6. РАСПРЕДЕЛЕННЫЕ СИЛЫ Понятие о силе, приложенной в точке, является идеализацией реальности. На самом деле взаимодействие тел всегда происходит по некоторой площадке или даже по объему (как у гравитационных сил). Говоря о сосредоточенной силе, которая приложена в точке, мы на самом деле имеем в виду равнодействующую некоторой распределенной силы. В механике рассматриваются три вида моделей распределенных сил: 1) силы, распределенные вдоль линии; 2) силы, распределенные по поверхности, и 3) силы, распределенные по объему. Рассмотрим первые два случая. Силы, распределенные вдоль линии Сила, распределенная вдоль линии, характеризуется ее интенсивностью Величина интенсивности может быть переменной Рис. 3.7 В общем случае, когда сила на участке (О, Рассмотрим частные случаи. Равномерно распределенная сила Если интенсивность постоянна q = const (см. рис. 3.7, б), то ее равнодействующая равна Сила, интенсивность которой меняется по линейному закону Рис. 3.8 В этом случае (рис. 3.8, а) соответствующий интеграл дает и равнодействующая будет проходить на расстоянии 2l/3 от вершины треугольника интенсивности и на расстоянии l/3 от его основания. Аналогично определяется равнодействующая, если с ростом координаты х интенсивность убывает от qmax до нуля. В случае, когда сила меняется по линейному закону от некторого значения Тогда исходная распределенная сила заменится двумя силами, линии действия которых делят участок (О, Силы, распределенные по поверхности Интенсивность такой силы называется давлением р и измеряется в паскалях: 1 Па = 1 Н/м2. В простейшем случае равномерно распределенной силы (рис. 3.9) на некотором участке поверхности ее равнодействующая будет равна, как известно, произведению давления на площадь этого участка А:
Рис. 3.9 В более сложном случае для определения равнодействующей требуется вычисление интеграла по площади.
Тема 4. СХОДЯЩИЕСЯ СИСТЕМЫ СИЛ 4.1. ПРИВЕДЕНИЕ СХОДЯЩЕЙСЯ СИСТЕМЫ СИЛ К РАВНОДЕЙСТВУЮЩЕЙ Сходящейся системой сил называются совокупность сил, линии действия которых пересекаются в одной точке, которую будем называть точкой схода системы. Простейшая система сходящихся сил (две силы) была рассмотрена в аксиоме параллелограмма сил (см. рис. 4.1), где говорилось, что их равнодействующая изображается диагональю параллелограмма, построенного на этих силах, и что она проходит через точку пересечения линий действия исходных сил. Рис. 4.1 Применение аксиомы параллелограмма можно обобщить на случай действия нескольких сходящихся сил. Так, на рисунке 4.2 показано, что при наличии трех сил мы можем сначала определить равнодействующую первых двух сил:
а затем, снова применяя аксиому параллелограмма, найти равнодействующую сил
По мере добавления новых сил можно каждый раз вновь использовать аксиому параллелограмма, предварительно перенося силы в точку схода системы. Каждый раз мы будем получать силу эквивалентную всей системе и, следовательно, являющуюся ее равнодействующей. Рис. 4.2. Линия действия полученной таким образом равнодействующей будет проходить через точку схода системы, а сама она будет равна геометрической сумме сил системы, то есть главному вектору:
Главный вектор, как известно, можно найти либо аналитически, либо путем построения силового многоугольника (рис. 4.2, б) Итак, как показано на рис. 4.3, система сходящихся сил всегда имеет равнодействующую, которая геометрически равна главному вектору этой системы и приложена в точке схода системы. Рис. 4.3 Это справедливо только для сходящихся систем сил. Для других систем сил равнодействующая может определяться иначе. Существуют системы сил, которые вообще не имеют равнодействующей, что означает, что такие системы сил невозможно заменить одной силой. Но нужно помнить, что
|
||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.132.107 (0.008 с.) |

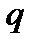 , которая определяется величиной силы, приходящейся на единицу длины (на 1м) и измеряется в Н/м.
, которая определяется величиной силы, приходящейся на единицу длины (на 1м) и измеряется в Н/м.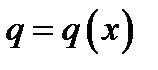 (рис. 3.7, а) или постоянной
(рис. 3.7, а) или постоянной 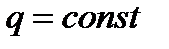 (рис. 3.7, б).
(рис. 3.7, б).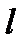 ) распределена по произвольному закону
) распределена по произвольному закону 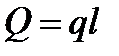 и приложена посередине участка распределения.
и приложена посередине участка распределения.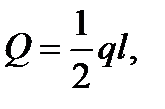
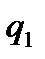 до значения
до значения 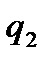 (рис. 3.8, б), силу удобно разбить на две распределенные силы, рассмотренные в пункте 2 (на рисунке разбиение показано штрихом).
(рис. 3.8, б), силу удобно разбить на две распределенные силы, рассмотренные в пункте 2 (на рисунке разбиение показано штрихом).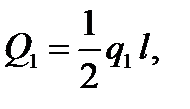 и
и 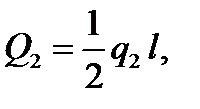
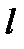 ) на три равные части.
) на три равные части.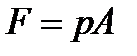 и будет проходить через центр тяжести этого участка поверхности.
и будет проходить через центр тяжести этого участка поверхности.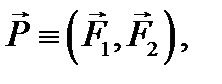
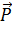 и
и 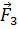 , линия действия которой также пройдет через точку О:
, линия действия которой также пройдет через точку О: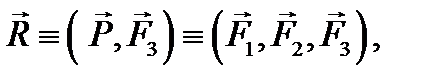
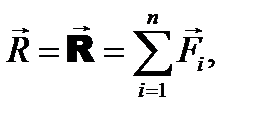 (4.1)
(4.1)


