Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая логика и теория множествСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ МНОЖЕСТВ · пересечение множеств соответствует логическому умножению, а объединение – логическому сложению ; ·
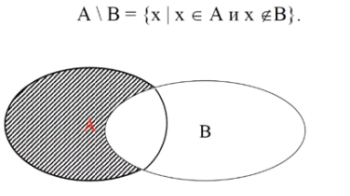
X ∨ U = U и X ∧ U = X · разностью двух множеств A и B называется новое множество, элементы которого принадлежат A, но не принадлежат B:
· дополнение множества X – это разность между универсальным множеством U и множеством X (например, для целых чисел X – все целые числа, не входящие в X)
· пусть требуется выбрать множество A так, чтобы выполнялось равенство A ∨ X = I; в этом случае множество A должно включать дополнение X, то есть A ≥ X (или A ⊇ X), то есть Amin = X пусть требуется выбрать множество A так, чтобы выполнялось равенство A ∨ X = I, в этом случае множество A должно включать дополнение X, то есть A ⊇ X; отсюда A ⊆ X, то есть Amax = X, Есть важнейшее свойство импликации- она показывает, что A это подмножество В (импликация является ложной тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно, т.е другими словами, если все элементы принадлежат В-, только тогда импликация истинна ) отсюда понятно что A min = B, а макс. совпадет с В A MAX = B
По закону исключенного третьего Если в задании формула тождественно истинна (равна 1), и Amin = B Где B — известная часть выражения. ,Если в задании формула тождественно истинна (равна 1), и Amax = B Где B — известная часть выражения. По закону противоречия Amax = B Где B — известная часть выражения. 2,Если в задании формула тождественно ложна (равна 0), и Amin = B Где B — известная часть выражения
(№ 365) На числовой прямой даны два отрезка: P=[35,55] и Q=[45,65]. Определите наименьшую возможную длину отрезка A, при котором формулы
(x ∈ P) → (x ∈ А) Аналогично для A + Q =1 А min =[45.65], как максимум вся числовая ось Или можно так По закону исключения третьего ИЛИ, Если в задании формула тождественно истинна (равна 1), и Amin = B Где B — известная часть выражения.
2 метод преобразования. При помощи импликации, импликация только тогда =1 когда оба его члена равны 1 (или утверждения истинны)или можно сказать что приP=[35,55] и Q=[45,65]. если x ∈ P то x ∈ A отсюда A=P если x ∉ A то и x∉Q отсюда A=Q Видим из первого А=[35,55] Из второго A=[45,65]. 6. Т.е как минимум A = P и A = Q, т.е Наименьшая длина будет при объединении P +Q === [35,65]=30, а как максимум вся числовая ось
Решение с помощью таблицы
Видим, что нужный отрезок это 35-65,там где А=1, длина 20.(там где ==1в обоих колонках) № 360) На числовой прямой даны три отрезка: P=[10,25], Q=[15,30] и R=[25,40]. Какова максимальная длина отрезка A, при котором формула МЕТОД 2 Или А →В=1 используя свойство импликации B включает в себя общие элементы (пересечние) с A В таких задачах, когда Здесь
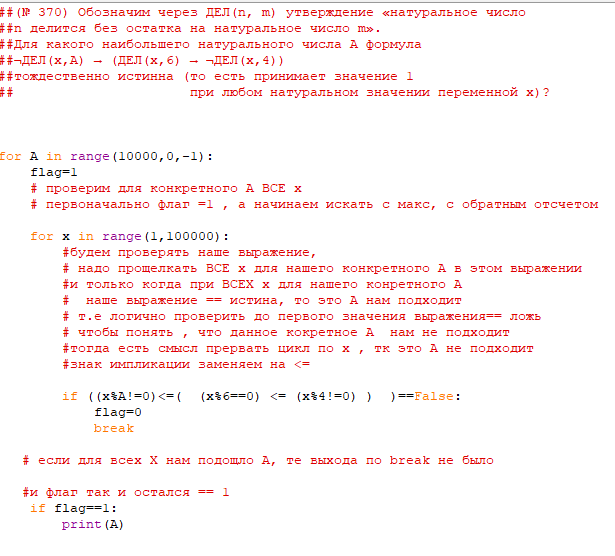
(№ 2242) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула (ДЕЛ(x, А) ∧ ДЕЛ(x, 6)) → ДЕЛ(x, 3) Ответ 12
(№ 384) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула Ответ 3. (№ 2259) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула
(ДЕЛ(x, 45) ∧ ДЕЛ(x, 15)) → ДЕЛ(x, A) Полезно знать А+А& B = A A &(A + B)= A A + ¬ A & B = A + B Утверждение 1. Логическое выражение ZK → ZM истинно для всех x тогда и только тогда, когда множество единичных битов двоичной записи числа M входит во множество единичных битов двоичной записи числа K.
(№ 22) Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула (x & 25 ≠ 0) → ((x & 17 = 0) → (x & А ≠ 0)) МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ МНОЖЕСТВ · пересечение множеств соответствует логическому умножению, а объединение – логическому сложению ; ·
X ∨ U = U и X ∧ U = X · разностью двух множеств A и B называется новое множество, элементы которого принадлежат A, но не принадлежат B:
· дополнение множества X – это разность между универсальным множеством U и множеством X (например, для целых чисел X – все целые числа, не входящие в X)
· пусть требуется выбрать множество A так, чтобы выполнялось равенство A ∨ X = I; в этом случае множество A должно включать дополнение X, то есть A ≥ X (или A ⊇ X), то есть Amin = X пусть требуется выбрать множество A так, чтобы выполнялось равенство A ∨ X = I, в этом случае множество A должно включать дополнение X, то есть A ⊇ X; отсюда A ⊆ X, то есть Amax = X, Есть важнейшее свойство импликации- она показывает, что A это подмножество В (импликация является ложной тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно, т.е другими словами, если все элементы принадлежат В-, только тогда импликация истинна ) отсюда понятно что A min = B, а макс. совпадет с В A MAX = B
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 745; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.213.119 (0.011 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

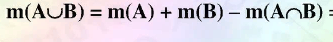












 это
это 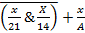 =
= 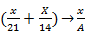
 стоит после импликации, значит оно включает в себя часть множеств, стоящие перед импликацией, -ищут НОК и плюс все делители НОК =42+ 21,14,7,6,3,2,1 понятно, что наиб. здесь НОК=42
стоит после импликации, значит оно включает в себя часть множеств, стоящие перед импликацией, -ищут НОК и плюс все делители НОК =42+ 21,14,7,6,3,2,1 понятно, что наиб. здесь НОК=42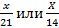 , а это НОК = 42
, а это НОК = 42