
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измеримые по Лебегу множества. Критерий измеримости.Содержание книги
Поиск на нашем сайте
Определение 1. Множество A Совокупность всех измеримых множеств обозначим через Заметим, что понятие измеримого множества зависит от исходноймеры m, заданной на алгебре K(S). Теорема 1. (Критерий измеримости). Пусть задано множество X и алгебра K(S) с σ -аддитивной конечной мерой m. Тогда для любого множества A Следствие1. Множество A Теорема 2. Совокупность Следствие 2. Счетное пересечение измеримых множеств измеримо. Теорема 3. Сужение внешней меры Таким образом, лебеговым продолжением меры m; заданной на алгебре K (K(S)) называется функция Определение 2. Мера m, заданная на алгебре K, называется полной, если из m(A) = 0 следует, что любое подмножество B Определение 3. Мера Определение 4. Множество A Следовательно, множество A Для измеримого множества A можно ввести определение меры множества по формуле
Можно показать, что значение
5. σ-аддитивность меры Лебега, σ -алгебра измеримых по Лебегу множеств. Пусть X – произвольное множество, K(S) ⊂ P(X) – алгебра его подмножеств, на которой задана σ-аддитивная конечная мера и для каждого множества A ⊂ X определена внешняя мера Определение Множество A ⊂ X называется измеримым по Лебегу относительно меры m, если для него выполнено равенство Теорема (Критерий измеримости). Пусть задано множество X и алгебра K(S) с σ-аддитивной конечной мерой m. Тогда для любого множества A ⊂ X следующие утверждения эквивалентны: 1) A измеримо по Лебегу относительно меры m; 2) для любого ε>0 существует элементарное множество B ∈ K(S) такое, что Следствие Множество A ⊂ X измеримо, если для любого ε > 0 существует измеримое множество B такое, что
Теорема Совокупность Σ измеримых по Лебегу множеств образует σ-алгебру множеств, содержащую исходную алгебру K(S). Следствие Счетное пересечение измеримых множеств измеримо. Теорема Сужение внешней меры Определение Мера m, заданная на алгебре K, называется полной, если из m(A) = 0 следует, что любое подмножество B ⊂ A принадлежит K и m(B) = 0. Определение Мера µ заданная на кольце K ⊂ P(X), называется σ-конечной, если существует последовательность множеств Определение Множество A ⊂ X называется измеримым относительно σ-конечной меры, если для любого n измеримо множество A ∩ An. Для измеримого множества A можно ввести определение меры множества по формуле
Можно показать, что значение
6. Непрерывность меры Лебега
14. Абсолютная непрерывность интеграла Лебега Теорема: Пусть f суммируемая функция на множестве А и пусть А = причем ряд справа сходится абсолютно. Следствие: Если f суммируема на измеримом множестве А, то f суммируема на любом подмножестве B
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1845; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.86.143 (0.005 с.) |

 X называется измеримым по Лебегу относительно меры m, если для него выполнено равенство
X называется измеримым по Лебегу относительно меры m, если для него выполнено равенство  (A) +
(A) +  . Если множество A измеримо, то назовем его мерой внешнюю меру, т. е.
. Если множество A измеримо, то назовем его мерой внешнюю меру, т. е.  (A) =
(A) = 
 > 0 существует элементарное множество B
> 0 существует элементарное множество B  B) <
B) < 
 .
. A2
A2  для всех n и X =
для всех n и X =  An.
An. An.
An. .
. (A) +
(A) +  ⊆
⊆  ⊆... ⊆
⊆... ⊆  ⊆... такая, что µ(
⊆... такая, что µ( .
.
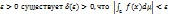 для всякого измеримого множества Е (А такого, что
для всякого измеримого множества Е (А такого, что  .
.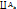 , где все
, где все  измеримые множества. Тогда f суммируема по каждому
измеримые множества. Тогда f суммируема по каждому 
 A;
A; функция f суммируема, причём ряд
функция f суммируема, причём ряд  сходится. Тогда функция f суммируема на А и
сходится. Тогда функция f суммируема на А и  -алгебре множества Х, называется знакопеременной мерой или зарядом.
-алгебре множества Х, называется знакопеременной мерой или зарядом.


