
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В результате решения уравнения теплопроводности была найдена такая функция, которая одновременно удовлетворяла уравнению и краевым условиям.Содержание книги
Поиск на нашем сайте
Полученная функция зависит от большого числа параметров, однако, анализ решения позволил сгруппировать эти величины в два безразмерных комплекса. Эти комплексы являются критериями подобия
В i = a × s / l; Fo = а × t / s 2 На основании второй теоремы подобия ( зависимость между переменными, характеризующими какой - либо процесс, может быть представлена в виде зависимости между критериями подобия ) искомая функция
может быть представлена в виде зависимости между критериями подобия q = ¦ (В i; Fo; Х).
32.Физический смысл критерия Фурье Критерий Фурье Fo = а × t / s 2 характеризует связь между временем прогрева системы, физическими свойствами и размерами тела, являясь мерой отношения теплового потока и скорости аккумуляции тепла, поступившего в систему. Эта связь ясна из следующей модификации критерия Фурье: если умножить числитель и знаменатель на S 2, то после перегруппировки критерий получает вид
Fo = =
 

 где - представляет количество тепла, поступившего за счёт теп- где - представляет количество тепла, поступившего за счёт теп-
- аккумулированное тепло. Иначе говоря, критерий Фурье оценивает скорость изменения температуры тела при нестационарном поле Из структуры Fo можно заключить, что при его неизменной величине время для нагрева или охлаждения зависит от линейных размеров тела t = Fo × s 2 / а и пропорционально s 2. 33.ФИЗИЧЕСКИЙ СМЫСЛ КРИТЕРИЯ БИО Критерий Био В i = a × s / l по своей структуре напоминает критерий Нуссельта, но является определяющим критерием, т.к. в него входят условия однозначности ( коэффициент теплоотдачи задается ). Критерий В i по физическому смыслу представляет меру отношения теп л ового сопротивления твёрдого тела s / l и теплового сопротивления 1 / a теплоотдачи в окружающую среду, что видно из его структуры
Или, критерий Био является мерой относительной интенсивности переноса тепла от омывающей среды на поверхности тела к переносу тепла в самом теле.
34.ГРАНИЧНЫЕ УСЛОВИЯ 1 ГО рода В этом случае задаётся распределение температуры по всей поверхности тела и изменение этого распределения во времени, т.е. задаётся функция Тпов = ¦ (t) или Тпов = ¦ (х, у, z, t). В частных случаях эта температура может быть постоянна во времени, t пов = const ( процессы нагрева или охлаждения с мгновенным изменением температуры поверхности тела, процессы выдержки ), или изменяться во времени, например, с постоянной скоростью t пов = t н + c × t, где С - скорость изменения температуры поверхности тела, 0С / час; t н - температура в начальный момент времени, 0С. На практике применяется в режимах термообработки. 36. РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ ПРИ ПОСТОЯННОЙ ТЕМПЕРАТУРЕ ПОВЕРХНОСТИ ТЕЛА Рассмотрим симметричный нагрев пластины неограниченной длины и ширины, но ограниченной толщины - 2 s и цилиндра бесконечной длины радиусом R. Граничные условия имеют следующий вид; t / x ± S = t п, или (15) t / r = R =t п, (16) где t п = const. Рассмотрим варианты начальных условий 1. На поверхности тела с одинаковой температурой по толщине, температура поверхности мгновенно изменяется до заданного значения и затем в процессе нагрева (охлаждения) поддерживается постоянной. Начальные условия имеют следующий вид: t / t = 0 = t н. (17) Графическое представление краевых условий.
Температура поверхности тела может мгновенно принять температуру окружающей среды при условии, что коэффициент теплоотдачи a будет очень большим, т.е. стремиться к ¥,следовательно, и интенсивность внешнего теплообмена будет настолько велика, что поверхность тела мгновенно примем температуру окружающей среды В результате заданной величиной оказывается температура поверхности тела, т.е. получаются граничные условия первого рода. Следовательно, критерий Био не является более параметром задачи. Лимитирующим звеном в процессе нагрева или охлаждения является внутренний теплообмен Подставляя (15) и (17) в общее решение уравнения теплопроводности (при граничных условиях первого рода) и произведя интегрирование и преобразование, получим решение для бесконечной пластины
t = t п + (t н - t п) ×

l = 1; 2; 3; ... - нормальный ряд чисел. В этом решении сумма бесконечного ряда может быть выражена как функция двух безразмерных параметров: величины критерия Фурье содержащего время t и симплекса х / s содержащего координату х
Значения F пл вычислены и представлены в виде графиков.

Решение для бесконечного цилиндра получим после подстановки граничных (16) и начальных (17) условий в общее решение уравнения теплопроводности t = t п + (t н - t п) ×
i 0 и I 1 - функции Бесселя нулевого и 1 го порядка.
q ц = F ц (Fo; X), где X = r / R. Значения функции F ц представлены в литературе в виде графиков. Если расчёт ведётся для установления температуры центра изделия, т.е. х / s = 0; r / R = 0, то расчётные уравнения примут вид:


Значения функций F пл с и F ц с также приведены в литературе. Есть в литературе и данные для различных значений х / s и r / R. Для бесконечной пластины температура в середине тела в момент времени t может быть найдена по формуле ( при а × t / S 2 ³ 0,06)

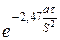
Для цилиндра бесконечной длины температура на оси может быть рассчитана по формуле ( при а × t / R 2 ³ 0,08)

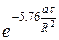
Рассмотренные граничные условия 1 го рода осуществляются на практике при очень большой интенсивности внешнего теплообмена. Например, при закалке в жидкостях, температура кипения которых ниже температуры нагрева под закалку. Или при нагреве в жидких металлах и соляных ваннах. Коэффициент теплоотдачи от изделия к жидкости имеет порядок a» 103 ¸ 104 Вт / м2 × К 2. Температура поверхности постоянна, но в начальный момент времени имеется распределение температур по сечению тела соответствующее параболе 2 го порядка. Граничные условия соответствуют граничным условиям, приведённым в 1 м варианте t / x ± S = t п; t / r = R =t п; t п = const
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.166.123 (0.012 с.) |






 (18)
(18)

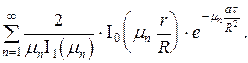 (19)
(19)



