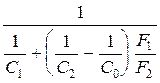Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Радиационный теплообмен в замкнутой системеСодержание книги
Поиск на нашем сайте Из двух серых поверхностей, разделенных Лучепрозрачной средой Как правило, основная задача теории радиационного теплообмена заключается в определении величины результирующего теплового потока на данной поверхности, если известны температуры и оптические константы всех поверхностей, составляющих данную систему. Рассмотрим теплообмен излучением между двумя серыми поверхностями произвольной формы, образующими замкнутую систему. Это означает, что излучение из данной системы не уходит и не поступает в неё из вне. Считаем, что обе поверхности имеют постоянную температуру Т1 и Т2 по всей площади F1 и F2. Теплообмен стационарный. С учетом замкнутой системы получаем QРЕЗ1 + QРЕЗ2 = 0, т. е. алгебраическая сумма результирующих потоков равна нулю. Это означает, что количество тепла, которое в единицу времени получает одна из поверхностей в результате теплообмена, равно тому количеству тепла, которое теряет другая поверхность. В связи с тем, что рассматриваемая система не обменивается излучением с окружающей средой, для неё справедливо выражение QРЕЗ2 = QПАД2 - QПАД1 или учитывая, что QПАД2 = Qэфф1 × j 1,2 QПАД1 = Qэфф2 × j 2,1 QРЕЗ2 = Qэфф1 × j 1,2 × - Qэфф2 × j 2,1 (27) Исключим из выражения (27) эффективные потоки, воспользовавшись формулой (6), в которой поглощательную способность А заменим на основании закона Кирхгофа степенью черноты e. В результате получим QРЕЗ2 = В этом выражении величина QС1 / e 1 равная отношению потока собственного излучения поверхности 1 к её степени черноты, представляет собой поток излучения абсолютно черного тела с поверхностью F1 и температурой T1, а величина QС2 / e 2 то же с поверхности F2 и температурой Т2. Используя закон Стефана - Больцмана QС1 / e 1 = С0 × (Т1 / 100)4 × F1; QС2 / e 2 = С0 × (Т2 / 100)4 × F2, (29) подставим выражения (29) в уравнение (28) и, учитывая, что QРЕЗ1 = - QРЕЗ2 находим результирующий тепловой поток на поверхности 2. QРЕЗ2 = Разделив числитель и знаменатель в правой части выражения (30) на коэффициент излучения абсолютно черного тела С0 и принимая во внимание, что в соответствии со свойством взаимности средних угловых коэффициентов излучения F1 × j 1,2 = F2 × j 2,1, получим QРЕЗ2 = где С1 = e 1 × С0 и С2 = e 2 × С0 - являются коэффициентами излучения серых поверхностей 1 и 2. Выражение (31) для результирующего теплового потока записывается обычно в виде QРЕЗ2 = Здесь СПР приведенный коэффициент излучения, который в общем случае для замкнутой системы, состоящей из двух изотермических поверхностей, имеет вид
СПР = Величина приведенного коэффициента излучения зависит от геометрической конфигурации системы, определяющей значение средних угловых коэффициентов излучения, и от оптических свойств поверхностей, определяющих значения коэффициентов излучения. Таким образом, в случае теплообмена излучением между двумя серыми поверхностями, образующими замкнутую систему, результирующий тепловой поток на любой из этих поверхностей пропорционален разности четвертых степеней их температур. Для замкнутых систем представленных на рисунках и характеризующихся тем, что j 1,2 = 1 формула для расчета результирующего потока принимает вид. QРЕЗ =
При этом для случая, показанного на рис. А (j 1,2 = j 2,1 = 1) приведённый коэффициент излучения принимает вид СПР = Для случаев Б и В (j 1,2 = 1; j 2,1 = F1 / F2) в виде СПР =
|
||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

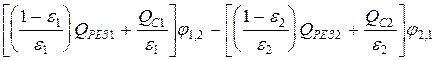 (28)
(28)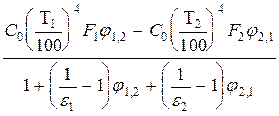 . (30)
. (30)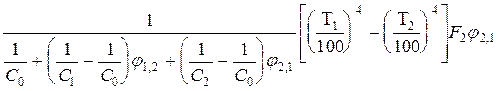 , (31)
, (31)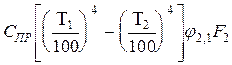 (32)
(32)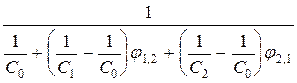 (33)
(33)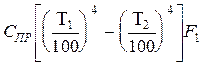 .
. 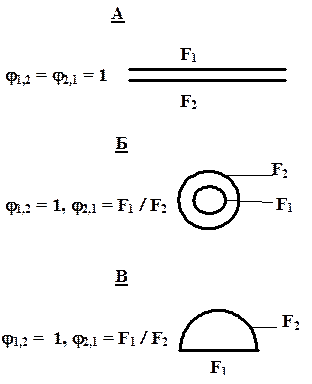
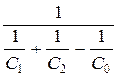 .
.