
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
А – горизонтальное положение; б – исходное положение.Содержание книги
Поиск на нашем сайте Рисунок 1 – Подъём портала Вес портала, приведенный к вершине,
где Go – вес дополнительного груза, полиспастов. Уравнение равновесия относительно точки O 1 во время подъёма портала:
Из геометрических преобразований изменяющаяся длина полиспаста АВ в зависимости от угла наклона портала
Усилие в полиспасте во время подъёма портала с учётом уравнений (2-3) будет иметь вид:
Тогда в начальный момент подъёма при φ = 0 усилие Sn будет максимальным:
Для определения угла подъёма портала φ = φ0, при котором начинается отрыв колонны от опоры, необходимо сделать следующие арифметические действия. Вес колонны, отнесённый к точке строповки:
Из условия равновесия при отрыве колонны от опоры относительно точки О следует:
Из уравнений (7-9) с учётом (4) получим угол наклона портала в момент отрыва колонны от опоры:
Усилие подъёма для произвольного положения аппарата найдём из условия: сумма элементарных работ всех приложенных к аппарату сил при любом его возможном перемещении должна быть равна нулю:
Из уравнения (11) получим зависимость для определения усилия подъёма:
где dh и d (AB) – соответствующие элементарные перемещения в направлении действия сил тяжести G к и силы подъёма Sn. Записывая уравнение (12) в дифференциальной форме и учитывая, что в процессе подъёма аппарата угол φ = const, и увеличивается только угол наклона колонны α, получим:
Для определения длины АВ воспользуемся уравнением в векторном виде для замкнутого контура системы AOO 1 BA (рис. 1, б):
Проектируя векторное уравнение (16) на оси координат ОХ и ОУ и возведя оба полученных уравнения в квадрат, а также, сложив их, получим:
Продифференцировав уравнение (17) по α, то есть d (AB)/ dα, и, подставляя в уравнение (13) значение dh / dα из уравнения (15) и d (AB)/ dα получим зависимость для определения усилия подъёма:
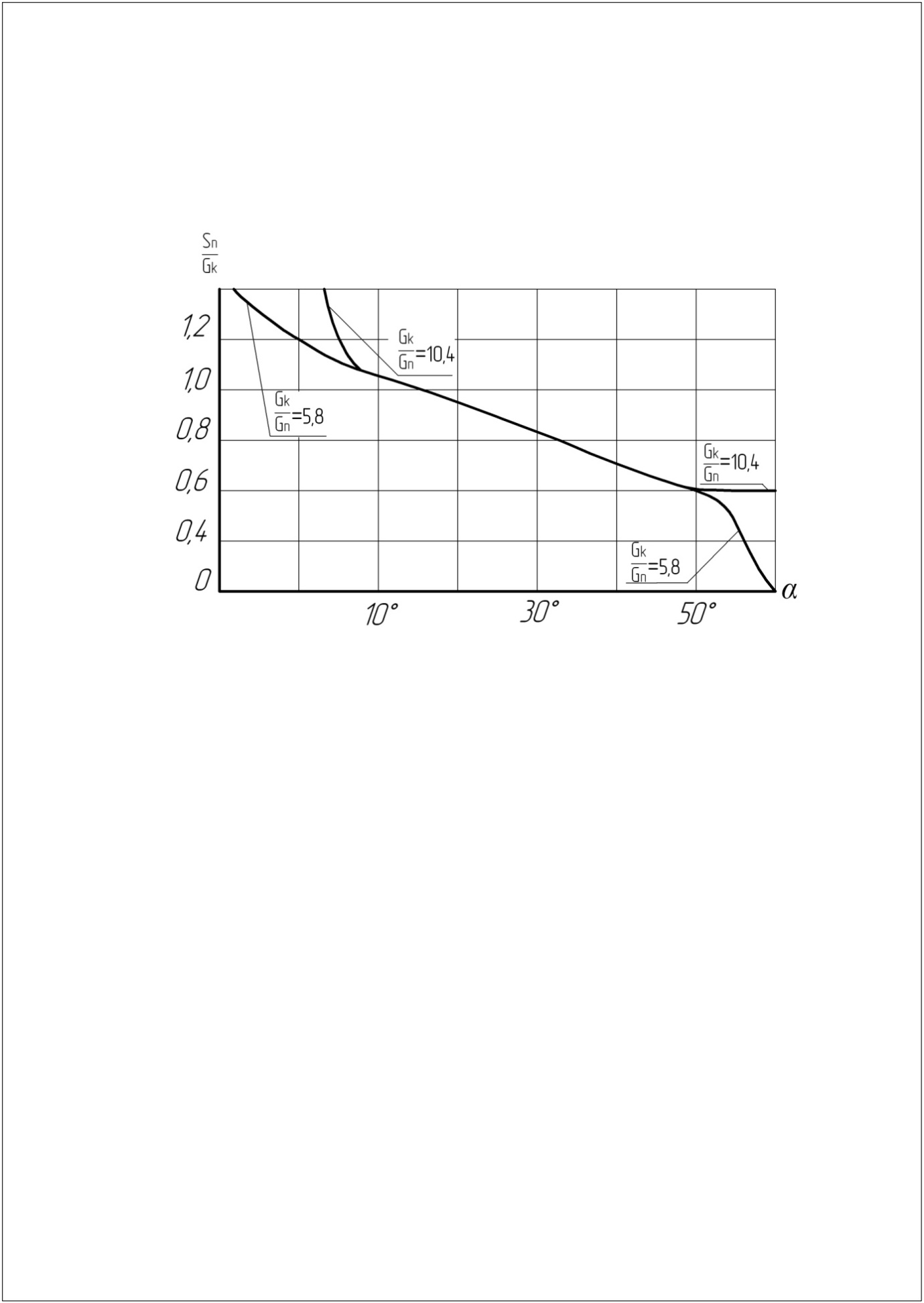
При соотношении Gk / Gn = 5,8÷10,4 – установка опор портала на одной вертикали с местом строповки аппарата – для упрощения расчётов усилия подъёма можно использовать график (рис. 2). При соотношений Gk / Gn > 10,4 расчёт проводить по формуле (18).
Рисунок 2 – График зависимости усилий от угла подъёма аппарата Усилие в шарнире определяется из зависимости:
где Для определения угла α0 неустойчивого равновесия системы колонна-портал рассмотрим равновесие этой системы. Система будет находиться в равновесии в том случае, когда потенциальная энергия её минимальна. Математически это адекватно соотношению:
где ln – расстояние от шарнира O 1 до точки приложения силы G 1 в положении неустойчивого равновесия. Неустойчивое равновесие системы колонна-портал наступит тогда, когда моменты от усилия в полиспастах относительно шарниров О и O 1 будут равны, то есть когда AB // OO 1:
Решая совместно уравнения (20) и (21), получим выражение для определения угла α0 неустойчивого равновесия:
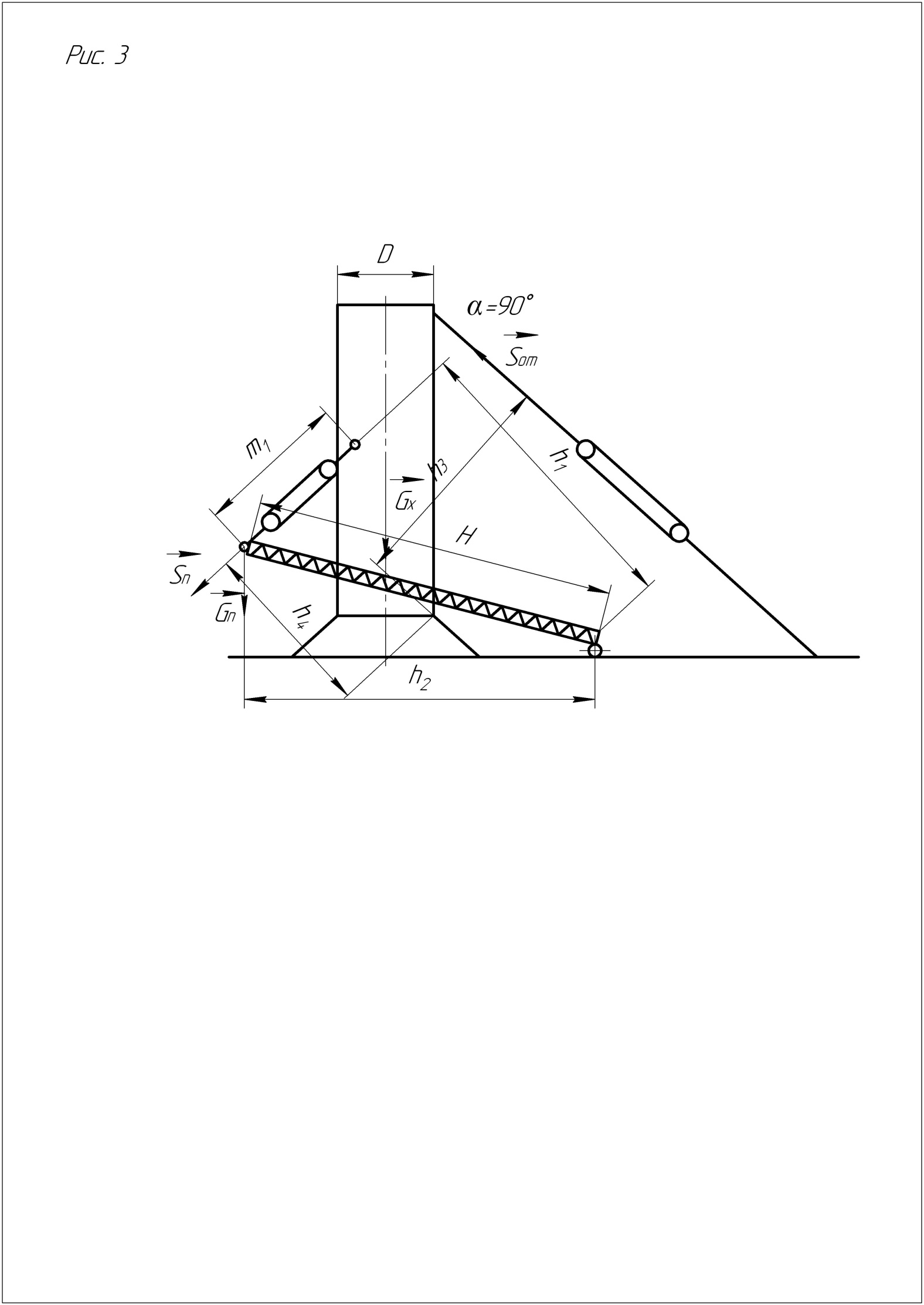
Зависимость (22) позволяет определить угол наклона аппарата в положении неустойчивого равновесия, в котором нагрузка на полиспасты стремится к нулю. Расчётную нагрузку в тормозной оттяжке при установке аппарата на фундамент можно определить как аналитическим, так и графоаналитическим методом (рис. 3). Для этого необходимо в масштабе изобразить положение аппарата, шевра и грузовых полиспастов и по выбранному масштабу определить размеры плеч. Размер m 1 определяется из условия Sn = 0 при положении неустойчивого равновесия.
Рисунок 3 – Расчётная схема усилия в тормозной оттяжке при установке аппарата на фундамент
Усилие в тормозной оттяжке определяется из уравнения:
|
||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

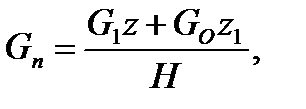 (1)
(1)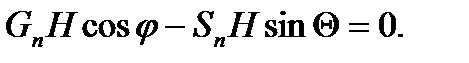 (2)
(2)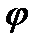 равна:
равна: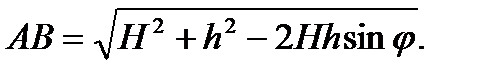 (3)
(3)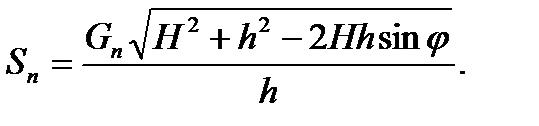 (4)
(4)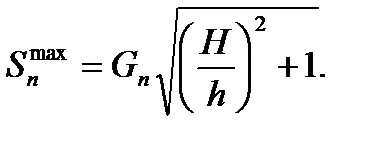 (5)
(5)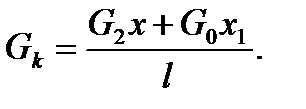 (6)
(6)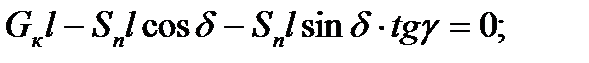 (7)
(7)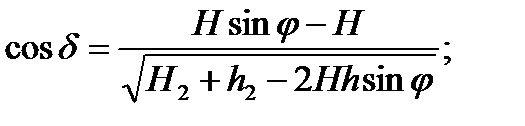 (8)
(8)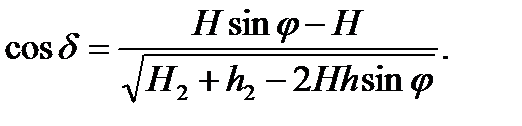 (9)
(9)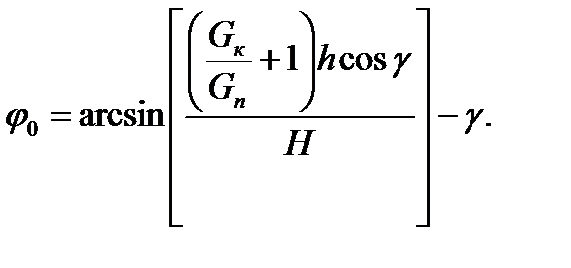 (10)
(10)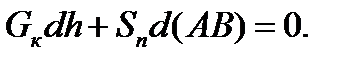 (11)
(11)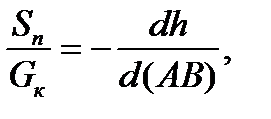 (12)
(12)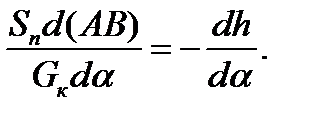 (13)
(13)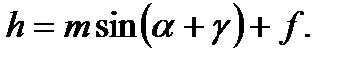 (14)
(14)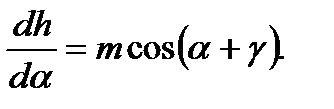 (15)
(15)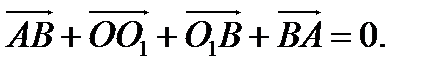 (16)
(16)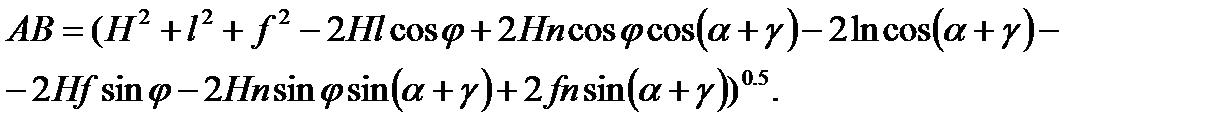 (17)
(17)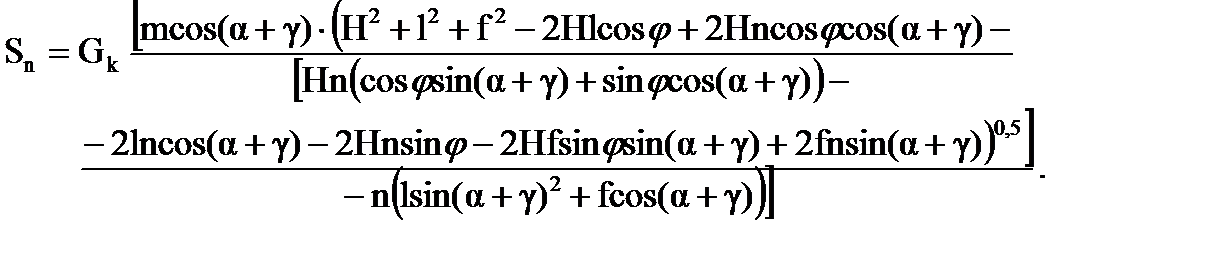 (18)
(18)
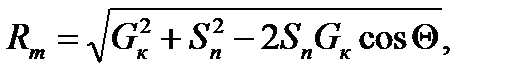 (19)
(19)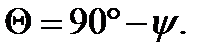
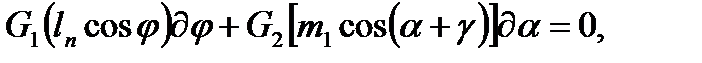 (20)
(20)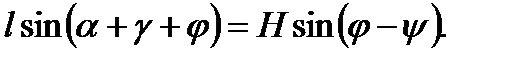 (21)
(21)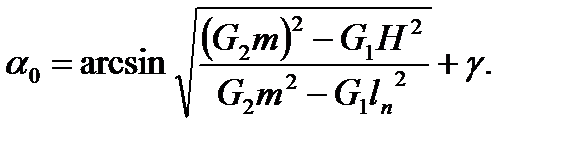 (22)
(22)
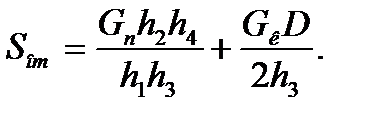 (23)
(23)


