
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные термодинамические параметрыСодержание книги
Поиск на нашем сайте
Состояние некоторой массы газа m определяется тремя термодинамическими параметрами: P, V, T. Здесь P -давление, V – объем, Т – температура. Закон, выражающий зависимость между этими параметрами, называется уравнением состояния газа: f (P, V, T) = 0. 2 Дополнительные термодинамические параметры:
Термодинамические процессы Изотермический процесс. Закон Бойля-Мариотта: При T = const; m = const; PV = const. Для 2-х состояний P 1 V 1 = P 2 V 2. Изобарический процесс. Закон Гей-Люссака: При P = const; m = const; V = V0 (1 + Для 2-х состояний Изохорический процесс. Закон Шарля: При V = const; m = const; P = P0 (1 + Для 2-х состояний Уравнение состояния идеального газа Для данной массы газа (закон Клапейрона)
Для 2-х состояний
Для любой массы газа (уравнение Клапейрона - Менделеева)
где N – число молекул; R = 8,31 Дж/(моль∙К) - универсальная газовая постоянная; k = 1,38´10–23 Дж/К – постоянная Больцмана; R = kN а,откуда следует
где n 0 – концентрация молекул. Закон Авогадро Моли любых газов при одинаковой температуре и давлении занимают одинаковые объемы. При нормальных условиях (P 0= 1,01×105 Па, T =273,15К); 6 Давление смеси газов (закон Дальтона):
где Pi – парциальное давление i-го газа, n – число газов в смеси. Масса 1 моля смеси газов:
где mi – масса i -го газа, входящего в смесь; 7 Основное уравнение кинетической теории газов:
где
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ТЕОРИИ ИДЕАЛЬНЫХ ГАЗОВ 1 Распределение молекул по скоростям (закон Максвелла): а) Число молекул, имеющих скорости в интервале от v до
где N – число всех молекул; m – масса молекулы; f (v) – функция распределения молекул по скоростям; e – основание натуральных логарифмов; k – постоянная Больцмана; б) Число молекул, относительные скорости которых заключены в интервале от u до
где Скорости молекул Наиболее вероятная Средняя арифметическая Среднеквадратичная 3 Средняя кинетическая энергия молекулы: а) для одноатомной молекулы б) число степеней свободы i молекулы: одноатомной i = 3 (3 поступат.); двухатомной i = 5 (3 поступат. + 2 вращ.); многоатомной i = 6 (3 поступат. + 3 вращ.); в) средняя энергия, приходящаяся на одну степень свободы:
г) средняя энергия любой молекулы:
|
||||
|
Последнее изменение этой страницы: 2021-04-14; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.72.27 (0.006 с.) |

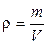 – плотность вещества;
– плотность вещества;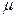 – молярная масса (масса одного моля);
– молярная масса (масса одного моля);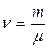 – число молей;
– число молей;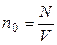 – концентрация молекул, где N число всех молекул в объеме V;
– концентрация молекул, где N число всех молекул в объеме V;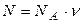 , где
, где 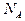 – число Авогадро (число молекул в 1 моле);
– число Авогадро (число молекул в 1 моле);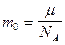 – масса одной молекулы любого вещества.
– масса одной молекулы любого вещества.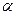 t);
t); 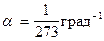 .
.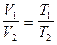 .
.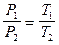 .
. .
.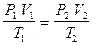 .
.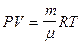 , или
, или  ,
,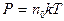 ,
, = 22,41×10–3 м3/моль.
= 22,41×10–3 м3/моль.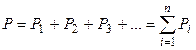 ,
,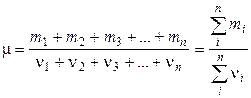 ,
, – число молей i -го газа, находящегося в смеси.
– число молей i -го газа, находящегося в смеси.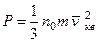 , или
, или 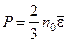 ,
,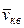 – среднеквадратичная скорость молекул;
– среднеквадратичная скорость молекул; 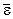 – средняя кинетическая энергия поступательного движения одной молекулы.
– средняя кинетическая энергия поступательного движения одной молекулы.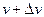 :
: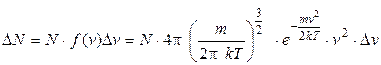 ,
, – вероятность того, что
– вероятность того, что 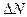 число молекул будут иметь скорости в интервале от v до
число молекул будут иметь скорости в интервале от v до 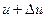 :
: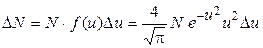 ,
,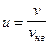 – относительная скорость; v – скорость молекул; v нв – наиболее вероятная скорость.
– относительная скорость; v – скорость молекул; v нв – наиболее вероятная скорость.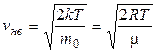 .
.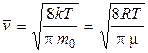 .
.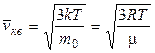 .
.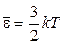 ;
;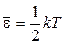 ;
;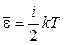 .
.


