Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа, Мощность, энергия. Законы сохраненияСодержание книги
Поиск на нашем сайте
I 1 Импульс материальной точкимассой m, двигающейся со скоростью
2 Центром масс системы тел называется точка c координатой
где mi - масса i -й материальной точки системы; ri - радиус вектор этой точки; N - число материальных точек системы. 3 Импульс тела
В случае поступательного движения импульс тела
где 4 Закон сохранения импульса для замкнутой системы
Закон сохранения импульса выполняется также для незамкнутых систем в следующих случаях: 1) если равнодействующая всех внешних сил, приложенных к системе, равна нулю, то сохраняется полный импульс системы; 2) если существует направление, проекция всех внешних сил на которое равна нулю, то сохраняется проекция импульса на это направление; 3) если время действия внешней силы очень мало, то полный импульс системы сохраняется. 5 Скорость изменения импульса системы равна сумме действующих на систему внешних сил
II Закон сохранения момента импульса 1 Момент импульса материальной точки относительно некоторой точки О
где m - масса материальной точки, движущейся со скоростью V; 2 Момент импульса твердого тела относительно оси вращения
где 3 Закон сохранения момента импульса для замкнутой системы
III Работа, мощность, энергия. Закон сохранения механической энергии 1 Работа переменной силы на пути S
В частном случае постоянной силы, действующей под неизменным углом a к перемещению,
2 Мощность
В случае постоянной мощности N = А /t, где А - работа, совершаемая за время t. 3 Кинетическая энергия тела (частицы), движущегося со скоростью V
4 Связь между силой, действующей на частицу в данной точке поля, и потенциальной энергией частицы
5 Потенциальная энергия тела массой m, поднятого над поверхностью Земли на высоту h П = mgh. 6 Потенциальная энергия упруго деформированного тела
где k - коэффициент упругости; x - величина деформации. 7 Закон сохранения механической энергии для консервативных систем Т + П = Е = const ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1 Свободно падающее тело в последнюю секунду своего падения проходит половину всего пути. Найти, с какой высоты падает тело, и какова продолжительность его падения. Решение Тело падает свободно, его ускорение равно 9,8 м/с2. Уравнение пути для тела, падающего с высоты h, начальная скорость которого равна нулю,
По условию задачи, тело за последнюю секунду проходит половину всего пути, значит, первую половину пути тело проходит за время (t -1) c. Для первой половины пути можно записать
Решим систему уравнений (1.1) и (1.2). Для этого подставим h из уравнения (1.1) в (1.2) и получим
Сокращая на g и раскрывая скобки, получаем квадратное уравнение относительно времени падения тела t t 2 - 4 t + 2 = 0. Решение этого уравнения дает два положительных корня: t 1 = 3,4 с и t 2 = 0,58 с. Второй корень не имеет смысла, так как по условию задачи тело падает больше 1 с. Для нахождения высоты, с которой падает тело, подставим t 1 = 3,4 с в уравнение (1.1)
2 Мальчик бросает мяч вверх под углом a = 70° к горизонту и попадает прямо в открытое окно, расположенное выше его плеча на расстоянии h = 9,6 м. Мяч влетает в окно горизонтально. Определить радиус кривизны траектории мяча в момент, когда он перелетает через подоконник, и начальную скорость мяча. Решение Тело, брошенное под углом к горизонту, движется по криволинейной траектории. Согласно принципу независимости движений, можно считать, что тело одновременно участвует в двух независимых движениях. Движение по горизонтали является равномерным, так как в этом направлении на тело не действуют силы (если пренебречь сопротивлением воздуха). Поэтому горизонтальная составляющая скорости V x = V 0cosa = const. Движение по вертикали под действием постоянной силы тяжести будет равнопеременным. Вертикальная составляющая скорости в начальный момент времени равна V y0 = V 0sina и изменяется с течением времени по закону равнозамедленного движения. В верхней точке траектории вертикальная составляющая скорости равна нулю. Так как по условию задачи мяч влетает в окно горизонтально, то в этот момент мяч находится в высшей точке траектории, для которой уравнения кинематики равнозамедленного движения принимают вид
Решаем эту систему уравнений относительно V 0, выражая t из второго уравнения и подставляя в первое. Получаем
Подставляя числовые значения, получим V 0=14,6 м/с. Для нахождения радиуса кривизны траектории в момент перелета мячом подоконника воспользуемся тем, что полное ускорение тела, брошенного в поле силы тяжести, равно g. В верхней точке траектории тангенциальное ускорение тела равно нулю и нормальное ускорение равно полному. Нормальное ускорение связано с радиусом кривизны траектории формулой a n = V 2 / R. В верхней точке траектории V = V 0cosa. Тогда
Подставляя числовые значения, получим R = 2,5 м.
3 Тело массой m = 10 кг движется по наклонной плоскости вверх с ускорением a. На тело действует сила F = 100 Н, направленная вверх под углом a=30° к поверхности наклонной плоскости. Коэффициент трения m = 0,1. Угол наклона плоскости к горизонту b = 30°. Определить ускорение тела. Решение
При решении динамических задач в большинстве случаев необходимо сделать чертеж и указать на нем все силы, действующие на тело. Запишем второй закон Ньютона в векторном виде Перейдем к скалярным уравнениям, для чего возьмем проекции всех векторных величин на оси X и Y: на ось Х: F cosa- F тр - mg sinb = ma, (3.1) на ось Y: N - mg cosb = 0 (3.2) Сила трения равна F тр = m N. (3.3) Решаем систему уравнений (3.1) - (3.3) относительно a
Подставляя числовые значения, получим a = 2,9 м/с2.
4 Шар массой 1 кг, движущийся горизонтально с некоторой скоростью V 1, столкнулся с неподвижным шаром массой 3 кг. Шары абсолютно упругие, удар прямой, центральный. Какую долю своей кинетической энергии первый шар передал второму? Решение
|
|||
|
Последнее изменение этой страницы: 2021-04-14; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 Закон изменения и сохранения импульса
Закон изменения и сохранения импульса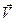 ,
,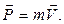


 - скорость движения центра масс.
- скорость движения центра масс.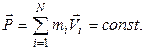

 ,
,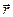 - радиус-вектор материальной точки; a - наименьший угол между векторами.
- радиус-вектор материальной точки; a - наименьший угол между векторами.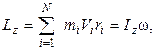
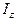 - момент инерции тела относительно оси z; w - угловая скорость тела.
- момент инерции тела относительно оси z; w - угловая скорость тела.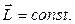

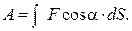
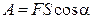 .
.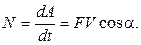
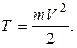
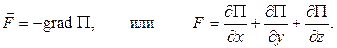
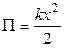 ,
,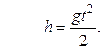 (1.1)
(1.1)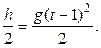 (1.2)
(1.2)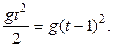
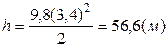 .
.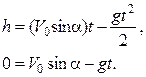 (2.1)
(2.1)
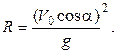

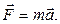 Или
Или 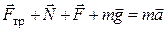 .
.