
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклость и вогнутость кривой. Точки перегиба.Содержание книги
Поиск на нашем сайте
Рассмотрим на плоскости кривую, которая является графиком дифференцируемой функции Определение 1. Кривая обращена выпуклостью вверх на интервале Кривая обращена выпуклостью вниз на интервале Кривую, обращенную выпуклостью вверх, будем называть выпуклой, а обращённую выпуклостью вниз – вогнутой.
Теорема 1. Если во всех точках интервала Теорема 2. Если во всех точках интервала Определение 2. Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба кривой. В точке перегиба касательная пересекает кривую, так как с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею. Теорема 3 (необходимое условие точки перегиба). Для того чтобы график функции Теорема 4 (достаточное условие точки перегиба). Пусть кривая определяется уравнением Пример: Найдите точки экстремума и точки перегиба функции Решение. Находим область определения функции: Первая производная функции равна:
Приравняем производную к нулю и найдем критические точки: Найдём значение функции в точке минимума Вторая производная функции равна:
Приравняем вторую производную к нулю и найдем точки: Найдём значения функции в точках перегиба: Результаты исследования сведены в таблицу:
Асимптоты. Определение. Прямая A называется асимптотой кривой, если расстояние
Различаются вертикальные (параллельные оси ординат) и наклонные асимптоты. 1) Вертикальные асимптоты. Если Пример: Найдите вертикальные асимптоты кривой Решение. Найдём область определения функции
Найдём односторонние пределы:
Прямые
2) Наклонные асимптоты. Пусть кривая Пример: Найдите асимптоты кривой Решение. 1) Найдём односторонние пределы:
2) Найдём коэффициенты k и b:
Получаем уравнение наклонной асимптоты
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.42.225 (0.009 с.) |

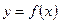 .
.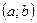 , если все точки кривой лежат ниже любой её касательной на этом интервале.
, если все точки кривой лежат ниже любой её касательной на этом интервале.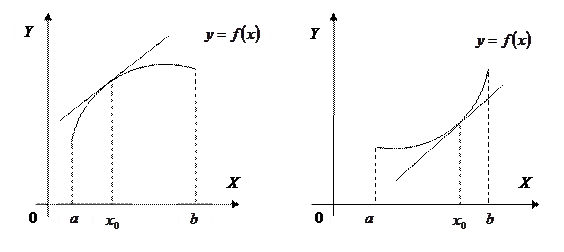
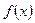 отрицательна, т.е.
отрицательна, т.е. 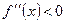 , то кривая
, то кривая 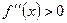 , то кривая
, то кривая 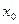 , необходимо, чтобы функция была дифференцируема в точке
, необходимо, чтобы функция была дифференцируема в точке 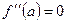 или
или 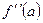 не существует и при переходе через точку
не существует и при переходе через точку 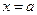 производная
производная 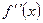 меняет знак, то точка кривой с абсциссой
меняет знак, то точка кривой с абсциссой 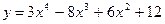 .
.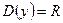 .
.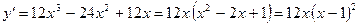 .
.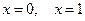 . При переходе через точку
. При переходе через точку 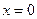 производная меняет знак с «-» на «+», значит, в этой точке функция имеет минимум. При переходе через точку
производная меняет знак с «-» на «+», значит, в этой точке функция имеет минимум. При переходе через точку 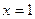 производная не меняет знака, следовательно, в этой точке функция не имеет экстремума.
производная не меняет знака, следовательно, в этой точке функция не имеет экстремума.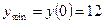 .
.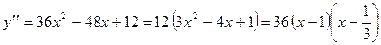 .
.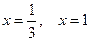 . При переходе через эти точки производная меняет знак, следовательно, они являются точками перегиба.
. При переходе через эти точки производная меняет знак, следовательно, они являются точками перегиба.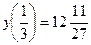 ,
, 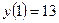 .
.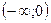
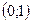
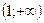
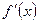
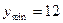
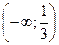
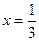
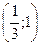
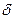 от переменной точки M кривой до этой прямой при удалении точки M в бесконечность стремится к нулю.
от переменной точки M кривой до этой прямой при удалении точки M в бесконечность стремится к нулю.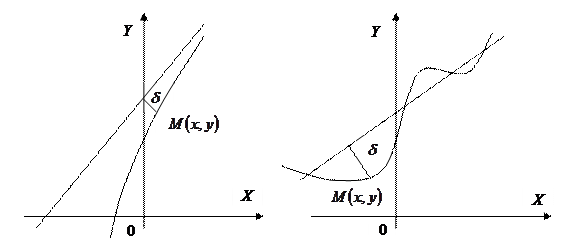
 ,
, 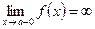 или
или 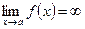 , то прямая
, то прямая 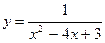 .
.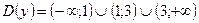
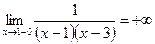 ;
; 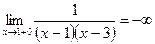 ;
;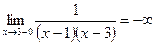 ;
; 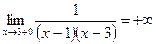 .
.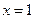 ,
, 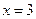 являются вертикальными асимптотами.
являются вертикальными асимптотами.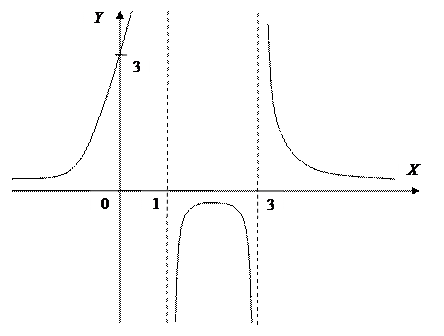
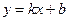 . Тогда
. Тогда 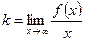 ,
, 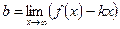 .
.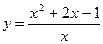 .
.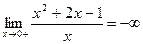 ;
; 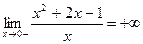 .
.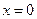 - вертикальная асимптота.
- вертикальная асимптота.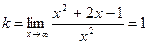 ;
; 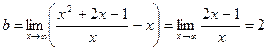 .
.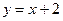 .
.


