
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
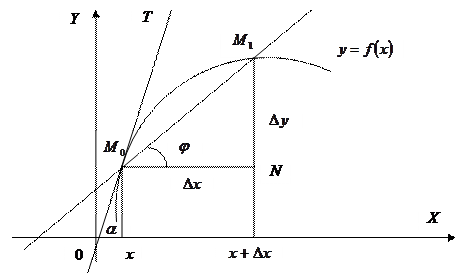
Геометрический смысл производной
Пусть
Определение. Касательной к линии Рассмотрим функцию Из прямоугольного треугольника
Следовательно, значение производной
Пример: Найдите тангенсы углов наклона касательной к кривой Решение.
Механический смысл производной
Если при прямолинейном движении точки задан закон движения
Пример: Материальная точка движется прямолинейно по закону Решение. В момент остановки скорость точки равна нулю. Находим
Тема 7. ДИФФЕРЕНЦИАЛ ФУНКЦИИ. ПРОИЗВОДНЫЕ РАЗЛИЧНЫХ ПОРЯДКОВ
Уравнения касательной и нормали
Возьмём на кривой
Для касательной угловой коэффициент
или
Определение. Нормалью к кривой в данной точке называется прямая, проходящая через данную точку перпендикулярно к касательной в этой точке. Согласно определению, угловой коэффициент нормали
Подставив
или
Уравнение (3) есть уравнение нормали к графику функции
Длина отрезка QM, заключённого между точкой касания и осью Ox, называется длиной касательной, а проекция этого отрезка на ось Ox (отрезок QP) называется подкасательной. Длина отрезка MR называется длиной нормали, а проекция PR этого отрезка на ось Ox называется поднормалью.
Пример: Напишите уравнение касательной и нормали к кривой Решение.
Получаем уравнение касательной Находим координаты точек
Дифференциал функции Пусть функция
Отсюда Тогда
Так как в общем случае
Таким образом, Таким образом,
Если
Отсюда
Формула (4) показывает, что производную Свойства дифференциала Теорема 1. Дифференциал суммы двух дифференцируемых функций
Теорема 2. Дифференциал произведения двух дифференцируемых функций
Теорема 3. Дифференциал частного двух дифференцируемых функций
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.135.224 (0.016 с.) |
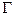 - дуга некоторой линии и
- дуга некоторой линии и 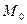 – точка этой линии,
– точка этой линии, 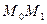 - секущая. Если точка
- секущая. Если точка 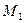 приближается по дуге
приближается по дуге 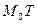 . Тогда прямая
. Тогда прямая 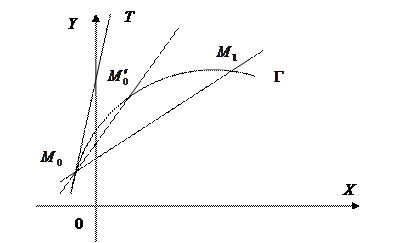
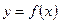 . Возьмём на графике функции точки
. Возьмём на графике функции точки 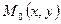 и
и 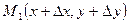 .
.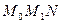 получаем
получаем 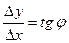 , тогда
, тогда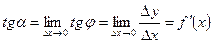 .
.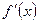 в данной точке x равняется тангенсу угла, образованному касательной к графику функции
в данной точке x равняется тангенсу угла, образованному касательной к графику функции 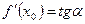
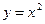 в точках
в точках 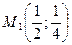 ,
, 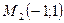 .
.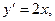
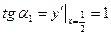 ,
, 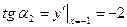 .
.
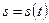 , то скорость движения в момент
, то скорость движения в момент 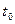 есть производная пути по времени:
есть производная пути по времени: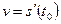 .
.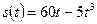 . Через сколько времени после начала движения точка остановится? Найдите путь, пройденный точкой до остановки.
. Через сколько времени после начала движения точка остановится? Найдите путь, пройденный точкой до остановки.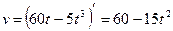 . Решаем уравнение
. Решаем уравнение 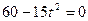 , т.е.
, т.е. 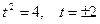 . Таким образом, после начала движения точка остановится через
. Таким образом, после начала движения точка остановится через 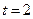 с. Путь, пройденный точкой до остановки, составит
с. Путь, пройденный точкой до остановки, составит 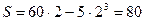 м.
м.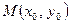 и напишем уравнение касательной к графику функции
и напишем уравнение касательной к графику функции 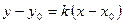 . (1)
. (1)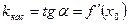 ,
, 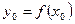 . Отсюда уравнение касательной к графику функции
. Отсюда уравнение касательной к графику функции 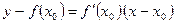
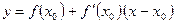 . (2)
. (2)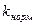 равен:
равен: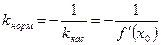 .
.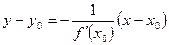
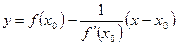 . (3)
. (3)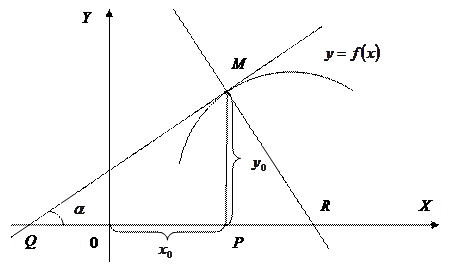
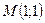 . Найдите длину подкасательной и поднормали.
. Найдите длину подкасательной и поднормали.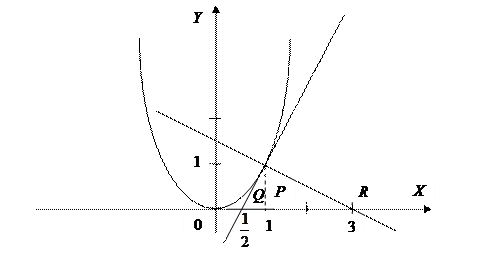
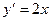 ,
, 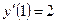 ,
, 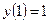 .
.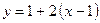 или
или 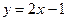 . Уравнение нормали имеет вид
. Уравнение нормали имеет вид 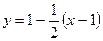 или
или 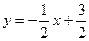 .
.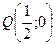 ,
, 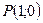 и
и 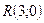 . Тогда длина подкасательной равна
. Тогда длина подкасательной равна 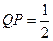 , а длина поднормали
, а длина поднормали 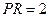 .
.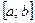 . Тогда для всех
. Тогда для всех  определена производная:
определена производная: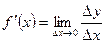 .
.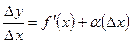 , где
, где 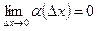 .
.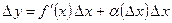 . (1)
. (1)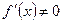 , то
, то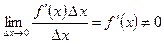 ,
, 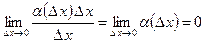 .
.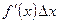 есть бесконечно малая величина одного порядка малости относительно
есть бесконечно малая величина одного порядка малости относительно 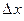 , а
, а 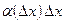 есть бесконечно малая величина высшего порядка относительно
есть бесконечно малая величина высшего порядка относительно 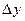 (по формуле (1)) есть главная часть приращения функции
(по формуле (1)) есть главная часть приращения функции 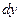 или
или 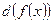 .
.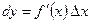 . (2)
. (2)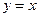 , то
, то 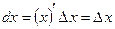 , отсюда
, отсюда 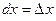 . Следовательно, дифференциал независимой переменной
. Следовательно, дифференциал независимой переменной 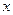 совпадает с её приращением. Формулу (2) можно записать в виде
совпадает с её приращением. Формулу (2) можно записать в виде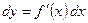 . (3)
. (3)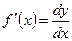 . (4)
. (4)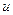 и
и 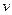 равен сумме дифференциалов этих функций:
равен сумме дифференциалов этих функций: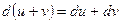 .
.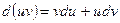 .
.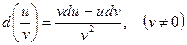 .
.


