
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление площади поверхности вращенияСодержание книги
Поиск на нашем сайте
Если дуга гладкой кривой
Если кривая задана параметрическими уравнениями
Если кривая задана в полярных координатах уравнением
Пример: Найти площадь поверхности, образованной вращением параболы
РАЗДЕЛ 5. варианты контрольных работ Самостоятельная работа №1 по теме «Непосредственное интегрирование» Вариант №1 1) Вариант №2 1) Вариант №3 1) Вариант №4 1) Вариант №5 1) Вариант №6 1) Вариант №7 1) Вариант №8 1) Вариант №9 1) Вариант №10 1) Вариант №11 1) Вариант №12 1) Вариант №13 1) Вариант №14 1) Вариант №15 1) Вариант №16 1) Вариант №17 1) Вариант №18 1) Вариант №19 1) Вариант №20 1) Вариант №21 1) Вариант №22 1) Самостоятельная работа №2 по теме «Замена переменной под знаком неопределённого интеграла» Вариант №1 1) Вариант №2 1) Вариант №3 1) Вариант №4 1) Вариант №5 1) Вариант №6 1) Вариант №7 1) Вариант №8 1) Вариант №9 1) Вариант №10 1) Вариант №11 1) Вариант №12 1) Вариант №13 1) Вариант №14 1) Вариант №15 1) Вариант №16 1) Вариант №17 1) Вариант №18 1) Вариант №19 1) Вариант №20 1) Вариант №21 1) Вариант №22 1) Вариант №23 1) Вариант №24 1) Самостоятельная работа №3 по теме «Интегрирование рациональных дробей» Вариант №1 1) Вариант №2 1) Вариант №3 1) Вариант №4 1) Вариант №5 1) Вариант №6 1) Вариант №7 1) Вариант №8 1) Вариант №9 1) Вариант №10 1) Вариант №11 1) Вариант №12 1) Вариант №13 1) Вариант №14 1) Вариант №15 1) Вариант №16 1) Вариант №17 1) Вариант №18 1) Вариант №19 1) Вариант №20 1) Самостоятельная работа №4 по теме «Интегрирование иррациональных выражений»
Самостоятельная работа №5 «Интегрирование по частям. Интегрирование тригонометрических функций» Вариант №1
Вариант №2
Вариант №3
Вариант №4
Вариант №5
Вариант №6
Вариант №7
Вариант №8
Вариант №9
Вариант №10
Вариант №11
Вариант №12
Вариант№1 3
Вариант№1 4
Вариант№ 15
Вариант№ 16
Вариант №17
Вариант №18
Вариант №19
Вариант №20
Вариант №21
Контрольная работа по теме «Дифференциальное исчисление» Вариант №1 1. Вычислить производные: 1) 2. Найти производную n-го порядка от функции 3. Найти приближённые значения: 1) 4. Найти пределы: 1)
Вариант №2 1. Вычислить производные: 1) 3) 2. Найти производную n-го порядка от функции 3. Найти приближённые значения: 1) 4. Найти пределы: 1)
Вариант №3 1. Вычислить производные: 1) 3) 2. Найти производную n-го порядка от функции 3. Найти приближённые значения: 1) 4. Найти пределы: 1)
Вариант №4 1. Вычислить производные: 1) 2. Найти производную n-го порядка от функции 3. Найти приближённые значения: 1) 4. Найти пределы: 1) Контрольное тестирование по теории функций одной переменной Вариант №1 1. Значение предела 1 2 0,5
0 2. Значение производной функции 0 -1 1 2 4 3. Найдите угловой коэффициент касательной, проведенной к графику функции 0 1 2 3 4 4. Точкой минимума функции
5. Найдите интеграл
6. Вычислить площадь фигуры, ограниченной линиями 12 11 13 10 14 Вариант №2 1. Значение предела 1 3 4 -1 0 2. Значение производной функции -1 1 0 0,25 0,5 3. Найдите угловой коэффициент касательной к кривой 1 32 8 16 4 4. Найдите точки экстремума функции 0; - 2 0 -2 1 0; - 1 5. Найдите интеграл
6. Площадь фигуры, ограниченной линиямиy=lnx, x=e, 1 3 2 6 4
Вариант №3 1. Значение предела 2 4 6 8 0 2. Значение производной функции 1 2 0,5 0 -2 3. Найдите угловой коэффициент касательной, проведенной к графику функции 10 14 -10 -14 0 4. Найдите точки перегиба функции нет 1 0 - 1 ±1 5. Найдите интеграл
6. Площадь фигуры, ограниченной линиями xy=4, x=1, x=4, y=0 равна
Вариант №4 1. Значение предела 1 0,25
2 0 2. Значение производной функции 1 2 3 4 5 3. Найдите угловой коэффициент касательной, проведенной к графику функции 1 -4 -1 4 0 4. Найдите точки перегиба функции 2; 4 2 2; 1 2; 2 Нет 5. Найдите интеграл
6. Площадь фигуры, ограниченной данными линиями
Вариант №5 1. Значение предела 1 0 2 -1
2. Значение производной функции
3. Найдите угловой коэффициент касательной, проведенной к графику функции 1 -5 -1 5 2 4. Найдите наибольшее и наименьшее значения функции 2; - 18 -2; - 18 2; -2 -2; 16 2; 0 5. Найдите интеграл
6. Вычислить площадь фигуры, ограниченной линиями 32/3 31/3 11 30/3 34/3
Вариант №6 1. Значение предела 0 10 15 20 5 2. Значение производной функции -4 0 6 4 1 3. Уравнение касательной, проведённой к графику функции y=2x y=1-x y=1-2x y=-2x y=2x+1 4. Найдите наибольшее и наименьшее значение функции 8; 0 4; 0 1; 0 1;4 8; 4 5. Найти интеграл
6. Площадь фигуры, ограниченной линиями
Вариант №7 1. Значение предела 1 0 1/8 1/3 1/7 2. Значение производной функции 2/3 1/3 -1/3 0 1 3. Уравнение касательной к кривой х+у-2=0 х=0 у=0 х+у-1=0 х+у+1=0 4. Найдите наибольшее и наименьшее значения функции 13; 4 13; 2 13; -2 13; 0 4; -2 5. Найдите интеграл
6. Площадь фигуры, ограниченной линиями
КОНТРОЛЬНЫЙ ТЕСТ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

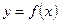 вращается вокруг оси OX, то площадь поверхности вращения вычисляется по формуле
вращается вокруг оси OX, то площадь поверхности вращения вычисляется по формуле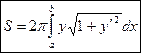 .
.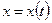 ,
, 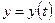 , где
, где 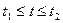 , то площадь поверхности вращения равна
, то площадь поверхности вращения равна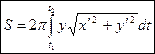 .
.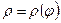 , где
, где 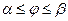 , то площадь поверхности вращения равна
, то площадь поверхности вращения равна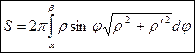 .
.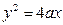 вокруг оси абсцисс от вершины до точки с абсциссой x =3 a.
вокруг оси абсцисс от вершины до точки с абсциссой x =3 a.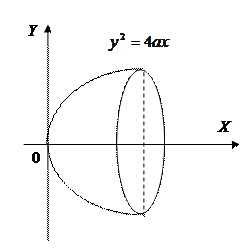
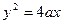 ,
, 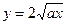 ,
, 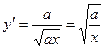 .
.
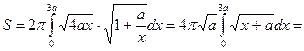
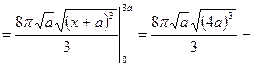
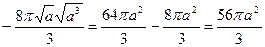
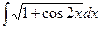 2)
2) 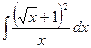
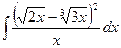 2)
2) 
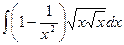 2)
2) 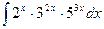
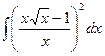 2)
2) 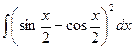
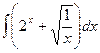 2)
2) 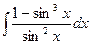
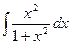 2)
2) 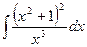
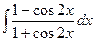 2)
2) 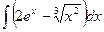
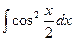 2)
2) 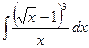
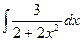 2)
2) 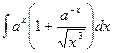
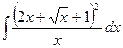 2)
2) 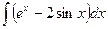
 2)
2) 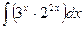
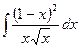 2)
2) 
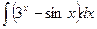 2)
2) 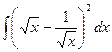
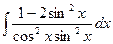 2)
2) 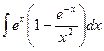
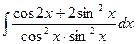 2)
2) 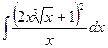
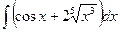 2)
2) 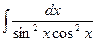
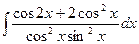 2)
2) 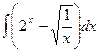
 2)
2) 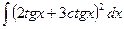
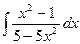 2)
2) 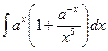
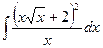 2)
2) 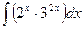

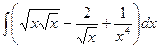 2)
2) 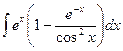
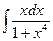 2)
2) 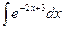
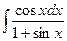 2)
2) 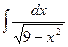
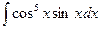 2)
2) 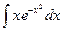
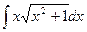 2)
2) 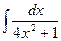
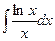 2)
2) 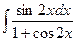
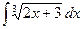 2)
2) 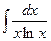
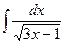 2)
2) 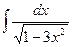
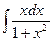 2)
2) 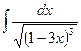
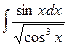 2)
2) 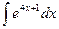
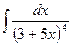
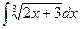 2)
2) 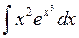 2)
2) 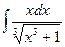
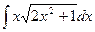 2)
2) 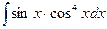
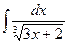 2)
2) 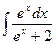
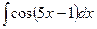 2)
2) 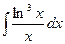
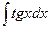 2)
2) 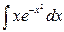
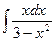 2)
2) 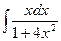
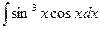 2)
2) 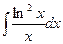
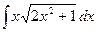 2)
2) 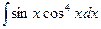
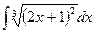 2)
2) 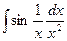
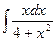 2)
2) 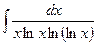
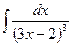 2)
2) 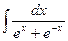
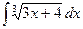 2)
2) 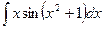
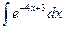 2)
2) 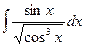
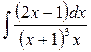 2)
2) 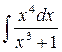
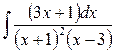 2)
2) 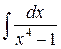
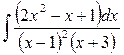 2)
2) 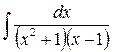
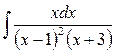 2)
2) 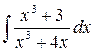
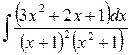 2)
2) 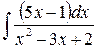
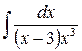 2)
2) 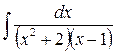
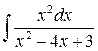 2)
2) 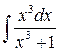
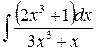 2)
2) 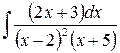
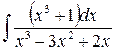 2)
2) 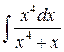
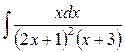 2)
2) 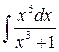
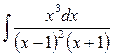 2)
2) 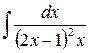
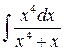 2)
2) 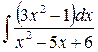
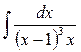 2)
2) 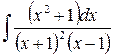
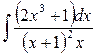 2)
2) 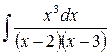 2)
2) 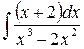
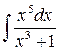 2)
2) 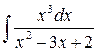
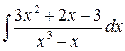 2)
2) 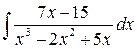
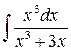 2)
2) 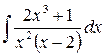
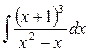 2)
2) 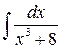
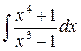 2)
2) 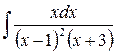
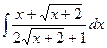
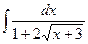
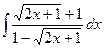
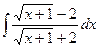
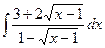
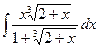
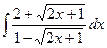
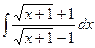
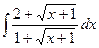

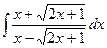
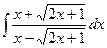
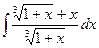
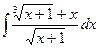
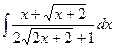
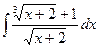
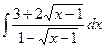
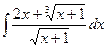
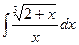
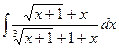
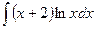
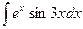
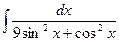

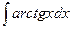
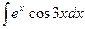
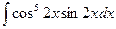
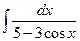
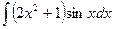
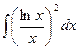
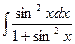
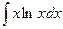
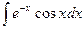
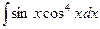
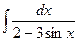
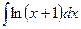
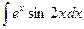
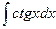
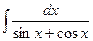
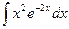
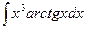
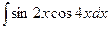
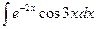
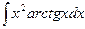
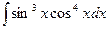
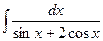
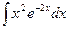
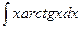
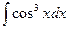
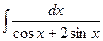
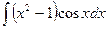
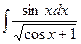
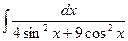
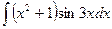
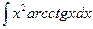
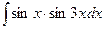
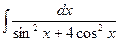
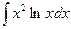
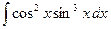
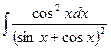
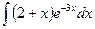
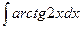
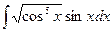
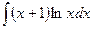
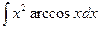
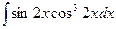
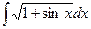
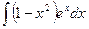
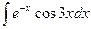
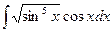

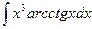
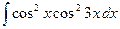
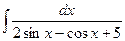
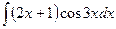
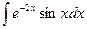
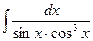
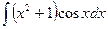
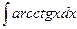
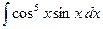
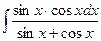
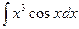
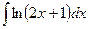
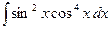
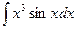
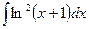

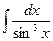
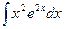
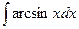
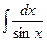
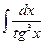
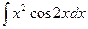
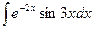
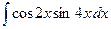
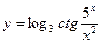 ; 2)
; 2) 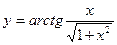 ; 3)
; 3) 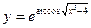 ; 4)
; 4) 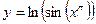 .
.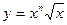 .
.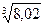 ; 2)
; 2) 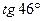 .
.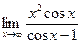 ; 2)
; 2) 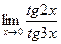 ; 3)
; 3) 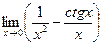 .
.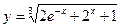 ; 2)
; 2) 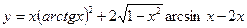 ;
;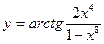 ; 4)
; 4) 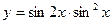 .
.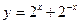 .
.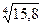 ; 2)
; 2) 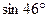 .
.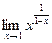 ; 2)
; 2) 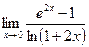 ; 3)
; 3) 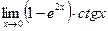 .
.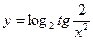 ; 2)
; 2) 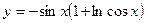 ;
; 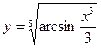 ; 4)
; 4) 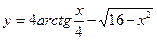 .
.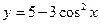 .
.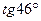 ; 2)
; 2) 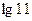 .
.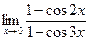 ; 2)
; 2) 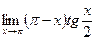 ; 3)
; 3) 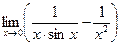 .
.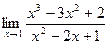 равно
равно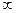
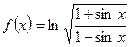 в точке
в точке 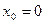 равно
равно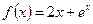 в его точке с абсциссой
в его точке с абсциссой 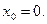
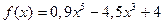 является точка х, равная
является точка х, равная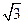
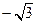 0 3 -3
0 3 -3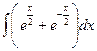
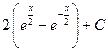
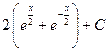
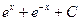
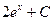
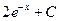
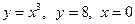
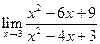 равно
равно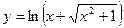 в точке
в точке 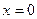 равно
равно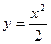 в точке A(8;32).
в точке A(8;32).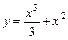 .
.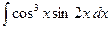

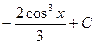
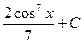
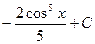
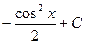
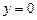 равна
равна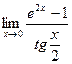 равно
равно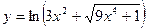 в точке
в точке 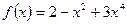 в его точке с абсциссой
в его точке с абсциссой 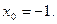
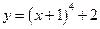 .
.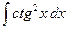 .
.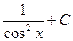
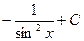
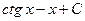
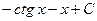
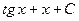
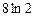
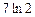 6 1
6 1 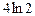
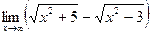 равно
равно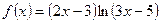 в точке
в точке 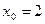 равно
равно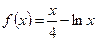 в его точке с абсциссой
в его точке с абсциссой 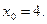
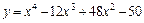 .
.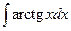 .
.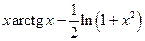
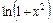
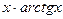
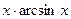
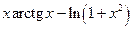
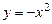 ,
, 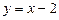 ,
, 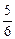
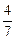
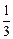
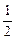
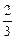
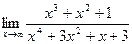 равно
равно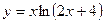 в точке
в точке  равно
равно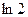
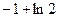
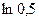
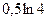
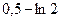
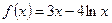 в его точке с абсциссой
в его точке с абсциссой 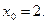
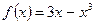 на отрезке [-2;3].
на отрезке [-2;3].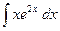 .
.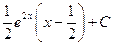
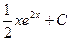
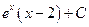
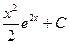
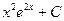
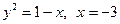
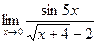 равно
равно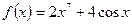 в точке
в точке 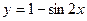 в точке с абсциссой
в точке с абсциссой 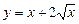 на отрезке [0;4].
на отрезке [0;4].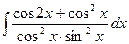 .
.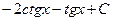
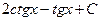
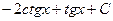
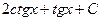
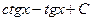
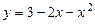 ,
, 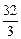
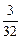 1 6 2
1 6 2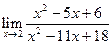 равно
равно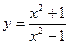 в точке
в точке 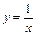 в точке х=1 имеет вид
в точке х=1 имеет вид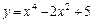 на отрезке [-2;2].
на отрезке [-2;2].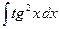
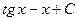
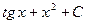
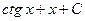
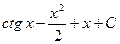
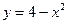 ,
, 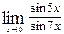 равно
равно
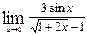 равно
равно
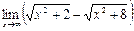 равно
равно
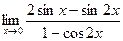 равно
равно
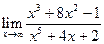 равно
равно
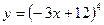 .
.
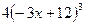
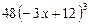
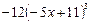
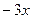
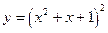 в точке
в точке 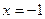 равно
равно
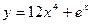 .
.
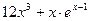
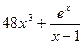
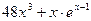
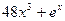
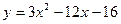 на отрезке [-3;8] равно
на отрезке [-3;8] равно
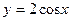 в точке с абсциссой
в точке с абсциссой 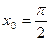 , имеет вид
, имеет вид
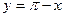 5)
5) 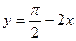
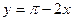
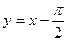
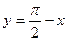
 в точке с абсциссой
в точке с абсциссой  , имеет вид
, имеет вид
 5)
5) 



 .
.
 является точка
является точка 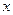 , равная
, равная
 .
.
 .
.
 .
.




 .
.




 .
.



