Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: подбор наиболее экономичного сечения балкиСодержание книги
Поиск на нашем сайте
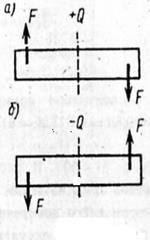
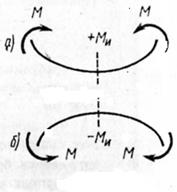
При деформации изгиба из условия прочности Цель работы: научиться определять внутренние силовые факторы при прямом изгибе, строить эпюры поперечных сил и изгибающих моментов. Уметь выполнять проектировочные и проверочные расчеты на прочность, выбирать рациональные формы поперечных сечений. Краткие теоретические сведения При прямом изгибе в поперечном сечении балки возникает два внутренних силовых фактора: изгибающий момент и поперечная сила. Поперечная сила в каком – либо поперечном сечении балки численно равна алгебраической сумме проекций на ось у внешних сил, действующих на балку по одну сторону от сечения. Изгибающий момент равен алгебраической сумме моментов сил, взятых с одной стороны от сечения относительно центра тяжести. Знаки поперечных сил Поперечная сила в сечении считается положительной, если она стремится развернуть сечение по часовой стрелке (рис.7а), если против - отрицательной (рис.7б) Знаки изгибающих моментов Если действующие на участке внешние силы стремятся изогнуть балку выпуклостью вниз, то изгибающий момент считается положительным (рис.8а), если выпуклостью вверх – отрицательным (рис.8б).
Рис.7 Рис.8 Правила, которыми следует руководствоваться при построении эпюр: 1. Эпюру моментов строят на сжатом волокне, т. е. положительные моменты (и положительные поперечные силы) откладывают вверх от оси, а отрицательные вниз. 2. Пользуясь принципом смягченных граничных условий, будем полагать, что в сечении, где приложена сосредоточенная сила, значение поперечной силы меняется скачкообразно, причем скачек равен модулю силы. 3. На том же основании, в сечении, где приложена пара сил, значение изгибающего момента меняется скачкообразно, причем скачек равен моменту пары. 4. На участке, где нет распределенной нагрузки, эпюра моментов, представляет собой наклонную прямую, а эпюра поперечных сил – прямую, параллельную оси. 5. На участке, где приложена равномерно распределенная нагрузка, эпюра моментов представляет собой параболу, а эпюра поперечных сил- наклонную прямую. 6. На конце балки изгибающий момент равен нулю, если там не приложена пара сил.
7. В точках, где поперечная сила равна 0, изгибающий момент принимает экстремальное значение Нормальные напряжения при изгибе:
Условие прочности при изгибе:
Моменты сопротивления для различных сечений: 1. Прямоугольник со сторонами b * h: W = bh2/ 6
2. Круг диаметром d: W = π d3/32 ≈ 0.1 d3 3. Кольцо D * d: W = π (D 4 – d 4) /32 D ≈ 0.1 (D 4 – d 4 ) / D
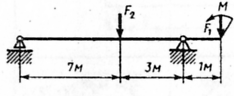
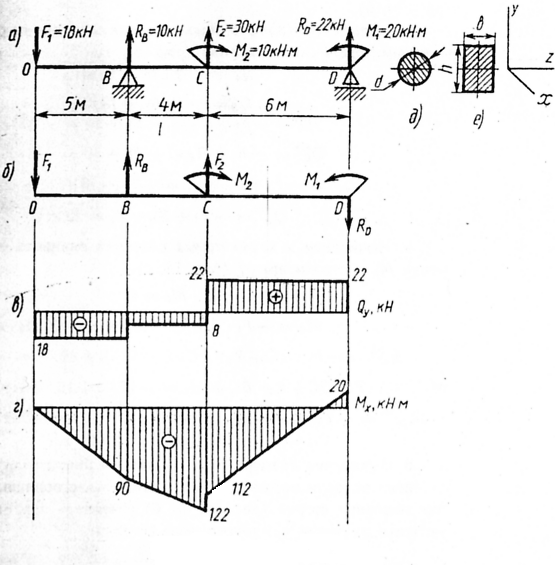
Пример решения задачи Пример. Для заданной двухопорной балки (рис.9,а)определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения (h, b, d) в форме прямоугольника или круга, приняв для прямоугольника h/b = 1,5.Считать [σ]= 160 Н/мм2. Решение 1. Определяем опорные реакции и проверяем их найденные значения:
Так как реакция RD получилась со знаком минус, то изменяем ее первоначальное направление на противоположное. Истинное направление реакции RD – вниз (рис.9,б). П р о в е р к а:
Условие статики 2. Делим балку на участки по характерным сечениям O, B, C, D (рис.6,б). 3. Определяем в характерных сечениях значения поперечной силы Qу и строим эпюру слева направо (рис.9,в):
Рис.9
4. Вычисляем в характерных сечениях значения изгибающего момента
5. Вычисляем размеры сечения данной балки из условий прочности на изгиб по двум вариантам: а) сечение – прямоугольник с заданным соотношением сторон (рис. 6, е) и двутавр; б) сечение – круг (рис.9,д) и швеллер. Вычисление размеров прямоугольного сечения:
Используя формулу
Используя формулу
Основываясь на значении Wх = 0,762·106 мм3 по таблице ГОСТ 8239-89 выбираем двутавр №40: момент сопротивления Wх = 953 см3; площадь сечения А = 72,6 см2. Выполняем сравнение по площади. Площадь сечения прямоугольника А = b·h = 1,5·12,72 = 242 см2.
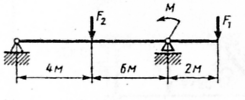
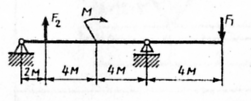
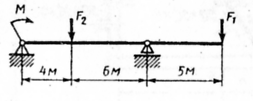
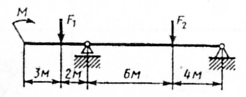
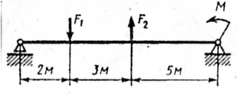
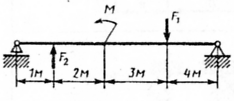
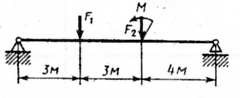
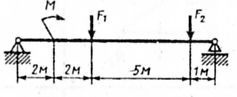
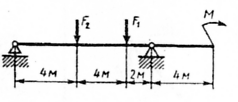
Задание для выполнения работы Для заданной двухопорной балки (рис.10) определить реакции опор, построить эпюры поперечных сил и изгибающих моментов. Подобрать из условия прочности размеры поперечного сечения прямоугольника и двутавра (нечетные варианты) или круга и швеллера (четные варианты), приняв для прямоугольника h=2b. Произвести сравнение выбранных сечений. Считать
Рис.10 Таблица 3
Схемы | F 1 | F 2 | M | ||||||||||||||||
| кН | кН*м | |||||||||||||||||||
| 1 | 1 | 20 | 10 | 12 | ||||||||||||||||
| 2 | 2 | 12 | 8 | 20 | ||||||||||||||||
| 3 | 3 | 10 | 20 | 15 | ||||||||||||||||
| 4 | 4 | 8 | 12 | 10 | ||||||||||||||||
| 5 | 5 | 16 | 8 | 25 | ||||||||||||||||
| 6 | 6 | 12 | 20 | 40 | ||||||||||||||||
| 7 | 7 | 8 | 16 | 15 | ||||||||||||||||
| 8 | 8 | 15 | 4 | 8 | ||||||||||||||||
| 9 | 9 | 40 | 20 | 30 | ||||||||||||||||
| 10 | 10 | 30 | 20 | 18 | ||||||||||||||||
| 11 | 1 | 25 | 6 | 5 | ||||||||||||||||
| 12 | 2 | 30 | 15 | 10 | ||||||||||||||||
| 13 | 3 | 18 | 24 | 12 | ||||||||||||||||
| 14 | 4 | 16 | 32 | 20 | ||||||||||||||||
| 15 | 5 | 24 | 30 | 5 | ||||||||||||||||
| 16 | 6 | 32 | 16 | 15 | ||||||||||||||||
| 17 | 7 | 50 | 22 | 22 | ||||||||||||||||
| 18 | 8 | 48 | 28 | 24 | ||||||||||||||||
| 19 | 9 | 36 | 24 | 18 | ||||||||||||||||
| 20 | 10 | 32 | 38 | 16 | ||||||||||||||||
| 21 | 1 | 28 | 18 | 12 | ||||||||||||||||
| 22 | 2 | 34 | 10 | 8 | ||||||||||||||||
| 23 | 3 | 10 | 14 | 15 | ||||||||||||||||
| 24 | 4 | 16 | 25 | 23 | ||||||||||||||||
| 25 | 5 | 18 | 36 | 45 | ||||||||||||||||
Порядок выполнения работы
1. Внимательно рассмотрите пример решения задачи.
2. Решите задачу по вариантам, взятым у преподавателя.
2.1. Начертите схему.
2.2. Определите значения опорных реакций..
2.3. Определите значения поперечных сил и постройте эпюру.
2.4. Определите значения изгибающих моментов и постройте эпюру.
2.5. Определите из условия прочности размеры поперечного сечения и номер прокатного профиля балки.
2.6. Выполните сравнение по расходу материала для подобранных сечений.
3. Выполните тестовые задания (вариант дает преподаватель) по теме 2.7 [2].
Оформление работы
1. Наименование и цель работы.
2. Решение задач с графическим оформлением.
3. При выполнении тестовых заданий, если выбор правильного ответа требует решения, то его нужно показывать.
Рекомендуемая литература
1. Олиферская В.П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий. – М.: ФОРУМ, 2013.
2. Олиферская В.П. Техническая механика: Сборник тестовых заданий. – М.: ФОРУМ, 2011
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №8
|
| Поделиться: |


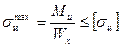
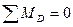 ;
;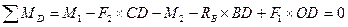
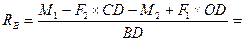
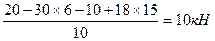
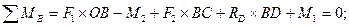
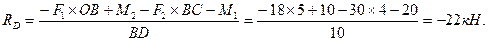
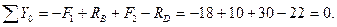
 выполняется, следовательно, реакции определены верно. При построении эпюр используем только истинные направления реакций опор.
выполняется, следовательно, реакции определены верно. При построении эпюр используем только истинные направления реакций опор.
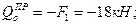
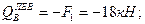
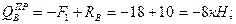
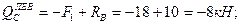
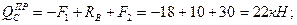
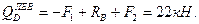

 и строим эпюру (рис.9,г):
и строим эпюру (рис.9,г):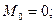
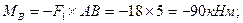
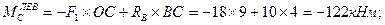
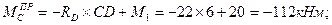
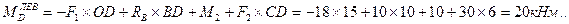
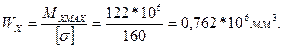
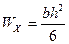 и учитывая, что h=1,5b, находим
и учитывая, что h=1,5b, находим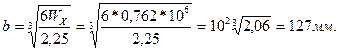
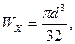 находим диаметр круглого сечения
находим диаметр круглого сечения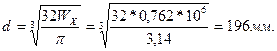
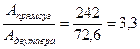
 =150 МПа, данные своего варианта взять из табл.3.
=150 МПа, данные своего варианта взять из табл.3.