
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Определение геометрических характеристик сеченияСодержание книги
Поиск на нашем сайте
Цель работы: Уметь определять главный центральный момент инерции сложных сечений. Краткие теоретические сведения Полярный момент инерции относительно полюса, лежащего в той же плоскости, называется взятая по всей площади сумма произведений элементарных площадок на квадраты их расстояний до полюса.
dA Jρ>0 Jρ≠0 ρ y
О х
1. Полярный момент инерции для круга d: Jρ = πd4/32 = 0,1d4 2. Полярный момент инерции для кольца: Jρ = π(D4 – d4)/32 = 0,1(D4 – d4), где D – наружный диаметр кольца; d – внутренний диаметр кольца.
Осевой момент инерции относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений элементарных площадок на квадрат их расстояния до этой оси. 1. Осевой момент инерции относительно оси Ох: 2. Осевой момент инерции относительно оси О y: Момент инерции сложной фигуры можно определить как сумму моментов инерции простых фигур. Осевые моменты инерции простых фигур: 1. Прямоугольника шириной в и высотой h Jx = в h 3 /12, Jу = h в3/12 2. Квадрата со стороной а: Jx = Jу = а4/12 3. Для круга диаметром d: Jx = J у = π d 4 /64 = 0,05 d 4 4. Для кольца с наружным диаметром D и внутренним диаметром d: Jx = J у = π(D4 – d 4) /64 = 0,05(D4 – d 4) Моменты инерции относительно параллельных осей Оси, проходящие через центр тяжести сечения называются центральными. Момент инерции относительно центральных осей называется центральным.
а
Моментинерции относительно какой – либо оси равен моменту инерции относительно центральной оси, плюс произведение площади фигуры на квадрат расстояния между осями. Главные оси – это оси, относительно которых осевые моменты инерции принимают экстремальные значения: максимальный и минимальный. Главные центральные моменты инерции рассчитываются относительно главных осей, проходящих через центр тяжести. Порядок выполнения работы 1. К выполнению задания приступить после рассмотрения примеров [3] стр. 140 – 144. 2. Выполнить расчетно-графическую работу 5 [3] стр. 144, предварительно взяв вариант у преподавателя. 3. 2. Выполните тестовые задания (вариант дает преподаватель) по теме 2.4 [2].
Содержание отчета 1. Наименование и цель работы. 2. Решение задач с графическим оформлением. 3. При выполнении тестовых заданий, если выбор правильного ответа требует решения, то его нужно показывать. Рекомендуемая литература 1. Олиферская В.П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий. – М.: ФОРУМ, 2013. 2. Олиферская В.П. Техническая механика: Сборник тестовых заданий. – М.: ФОРУМ, 2011 3. Сетков В.И. Сборник задач по технической механике. – М.: Издательский центр «Академия», 2010.. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.124.23 (0.009 с.) |


 у Jρ = ∫А ρ2·dA
у Jρ = ∫А ρ2·dA

 x [Jρ] = [ρ2][А] = м2·м2 = м4
x [Jρ] = [ρ2][А] = м2·м2 = м4 
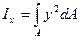
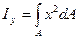
 y
y Ix = Ixo + Aa2
Ix = Ixo + Aa2

 x0
x0 x
x


