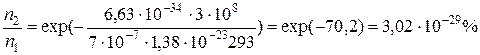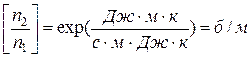Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий алгоритм решения задач по физикеСодержание книги
Поиск на нашем сайте
Решение любой задачи по физике можно разделить на следующие этапы. 1. Краткое представление условия задачи. Оно заключается в записи известных и искомых величин, где приводятся численные данные в том виде, в котором они имеются в условии задачи. Здесь же указываются сведения, заданные неявно (например, в графической или табличной формах). 2. Перевод всех данных в условии величин в единую систему единиц – обычно в Международную систему единиц (СИ). 3. Графическое изображение условия задачи, которое позволяет не только наглядно представить условие задачи, но и правильно определить некоторые параметры изучаемой системы (например, направление векторных величин или их проекции). Чтобы показать соотношение изображаемых величин, следует соблюдать приблизительный масштаб. (Например, при изображении нескольких векторов их длина должна быть приблизительно пропорциональна известным модулям этих векторов.) 4. Аналитическое решение задачи. На этом этапе, прежде всего, следует установить, какие физические закономерности лежат в основе данной задачи. Начинать советуем с формулы, которая содержит искомую величину. Затем из формул, выражающих эти закономерности, надо найти решение задачи. При этом следует придерживаться известного положения: число уравнений в составляемой системе уравнений должно быть равно числу неизвестных. Решая аналитически эту систему уравнений любым удобным методом, нужно получить расчетную формулу искомой величины. 5. Проверка размерности искомой величины. Прежде чем производить вычисления, необходимо проверить размерность полученного результата. Для этого в расчетную формулу вместо физических величин подставляют их единицы измерения. Проверка положительна, если после упрощения выражения получена единица измерения искомой величины. Если нет, то надо искать ошибку в преобразованиях при выводе расчетной формулы. 6. Вычисление. Численный результат получается путем подстановки численных значений известных величин в расчетную формулу и вычислением полученного арифметического выражения. Расчеты, как правило, упрощаются, если величины представить в виде небольшого числа и множителя, отражающего десятичный порядок данной величины. Например,
12300 = 1,23×104 или 0,00123 = 1,23×10–3. При вычислениях следует использовать микрокалькулятор. Результат округляется до трех значащих цифр. В пособии по решению задач в начале каждой темы приводятся особенности выполнения третьего и четвертого пунктов «Общего алгоритма». Этим учитывается специфика решения задач по каждой теме. Кроме того, при решении конкретной задачи какие-то этапы «Общего алгоритма» могут отсутствовать, но следовать единому алгоритму решения необходимо. Представленная последовательность действий может быть полезной при решении как расчетных, так и качественных задач. Пример оформления решения задачи Условие задачи: Оцените относительную населенность зоны проводимости полупроводника при комнатной температуре, если длина волны излучения п/п лазера 700 нм.
Таблица 2
Задание по контролю самостоятельной работы оформляется в рукописном виде. Пример оформления решения задачи приведен в таблице 2. После решения задач, входящих в задание, листы с решениями брошюруются и снабжаются титульным листом с обязательным указанием дисциплины, номера варианта задания и данных студента. При представлении задач обязательными элементами являются: – текст задачи и числовые исходные данные; – расчётные формулы; – проверка размерностей. В процессе защиты задания по контролю самостоятельной работы студентам могут быть предложены контрольные вопросы и задачи из соответствующего раздела курса.
Небрежно оформленные и выполненные не по своему варианту задания по контролю самостоятельной работы к защите не принимаются. Выполнение заданий по контролю самостоятельной работы максимально приближает обучение к практическим интересам с учетом имеющейся информации и является результативным методом закрепления знаний. Далее приведены основные формулы, примеры оформления и контрольные задачи по разделам физики.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.151.211 (0.007 с.) |
|||||||||||||||||

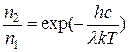 .
.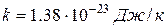 – постоянная Больцмана, λ – длина волны, излучаемая двухуровневой системой, Т – температура. Считая п/п лазер двухуровневой системой, определим из этого выражения относительную населенность зоны проводимости полупроводника. Подставляем численные значения:
– постоянная Больцмана, λ – длина волны, излучаемая двухуровневой системой, Т – температура. Считая п/п лазер двухуровневой системой, определим из этого выражения относительную населенность зоны проводимости полупроводника. Подставляем численные значения: