
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное решение алгебраических и трансцендентных уравненийСодержание книги
Поиск на нашем сайте
В трансцендентных уравнениях неизвестные входят под знаком трансцендентных функций, то есть неалгебраических, то есть тригонометрических показателей и др. Пусть дано уравнение
где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0, называется корнем уравнения (1) или нулем функции f(x). Будем предполагать, что уравнение (1) имеет лишь изолированные корни, то есть для каждого корня уравнения (1) существует окрестность, не содержащая других корней этого уравнения. Приближенное нахождение изолированных действительных корней уравнения (1) складывается обычно из двух этапов:
Для отделения корней используются следующая теорема: Теорема Если непрерывная функция f(x) принимает значение разных знаков на концах отрезков [a, b], то есть Процесс нахождения корней Определяем знаки функции f(x) в ряде точек из области определения функции х1,х2,х3,…, выбор которых учитывается особенностью функции f(x). если окажется, что Пример: Определить действительные корни уравнения:
На отрезке [2,3] имеется корень уравнения, так как Для отделения корней можно использовать графические методы. Нахождение корней методом половинного деления Пусть дано уравнение f(x)=0, (1)
Если f(x1) ≠0 то для продолжения вычисления выберем ту из частей данного отрезка [a, х1] или [х1, b]. Концы нового отрезка обозначим через a1 и b1 .
Продолжаем процесс пока не получим либо точный корень уравнения (1) либо не достигнуто значение с заданной точностью. Для оценки точности используется соотношение:
Из (2) получаем:
Пример: Методом половинного деления с точностью ε = 10-2 найти корень уравнения
Заданная точность достигается на седьмом шаге. х7 =0.8828125 с погрешностью d7=0,0078125<ε=0.01
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 90; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.42.247 (0.005 с.) |

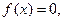 (1)
(1)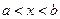 .
.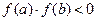 , то внутри этого отрезка находится по крайней мере один корень уравнения f(x)=0. если производная
, то внутри этого отрезка находится по крайней мере один корень уравнения f(x)=0. если производная 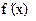 сохраняет свой знак на отрезке [a, b], то корень будет единственный.
сохраняет свой знак на отрезке [a, b], то корень будет единственный.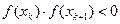 , то на отрезке [xk,xk+1], то имеется по крайней мере один корень уравнения f(x)=0. Необходимо каким-либо способом проверить, является ли этот корень единственным.
, то на отрезке [xk,xk+1], то имеется по крайней мере один корень уравнения f(x)=0. Необходимо каким-либо способом проверить, является ли этот корень единственным.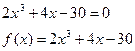
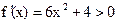 при всех х, то этот корень единственный.
при всех х, то этот корень единственный.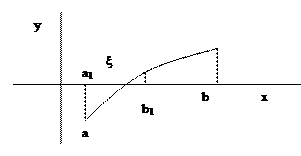 Причем f(x) непрерывна на отрезке [a, b] и
Причем f(x) непрерывна на отрезке [a, b] и 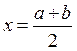
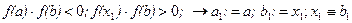
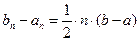 (2)
(2)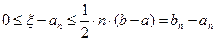 (3)
(3)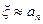 с погрешностью ε не превышающей
с погрешностью ε не превышающей 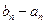
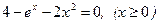
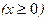
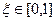 +1
+1
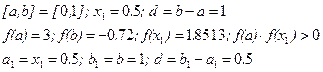
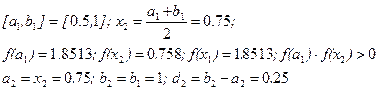
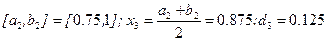
 и т.д.
и т.д.


