Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра вычислительной техникиСтр 1 из 17Следующая ⇒
Факультет кибернетики Кафедра вычислительной техники
КУРС ЛЕКЦИЙ по дисциплине ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Направления подготовки: - 654600 “Информатика и вычислительная техника” - 654700 “Информационные системы” Специальности: 2201 “Вычислительные машины, комплексы, системы и сети ” (ЭВМ) 2202 “Автоматизированные системы обработки информации и управления ” (АСУ) Информационные системы в технике и технологиях ” (МЭИ)
ЛЕКЦИЯ 1 Приближенные числа.
«В численных расчетах всегда есть бездна ловушек…» Форсайт, Малькольм, Моулер.
1. Источники погрешностей результатов вычислений. а) исходные данные получены из эксперимента, т.е. имеют ограниченную точность; б) в процессе вычислений иррациональные величины: π, е, в) часто методы решения задач требуют для получения ответа бесконечного числа шагов (например при интегрировании, когда исходная функция заменяется степенным рядом с бесконечным числом членов). Решение прекращается после выполнения конечного числа операций; г) ограниченное число разрядов в ЭВМ и т.д.
При решении задач на ЭВМ пользуются те или иные вычислительные схемы. Пример, «ловушки» при численных расчетах [Березин, Жидков, т 1 стр. 39] Вычислить объем шара, заключенного между цилиндром радиуса R и взаимно перпендикулярными плоскостями. Радиус шара – r.
Рассмотрим три различных вычислительных схемы:
Подсчитаем три выражения для двух приблизительных значений
1. 2. второе значение более точное. Результаты сведем в таблицу
Имеем 6 ответов (от -0,1666 до +1), существенно отличающихся друг от друга. Причем вариант -
Один программист сказал: «написать две хороших подпрограммы на порядок легче, чем решить, какая из них лучше» [Малькольм, Форсайт, Моулер]
Необходимость оценивать результаты программ обусловила необходимость анализа погрешностей.
2. Абсолютная и относительная погрешности, Под ошибкой или погрешностью, ∆а приближенного числа, а понимают разность между точным числом и приближенным
∆а = А – а (иногда: ∆а = а – А)
Абсолютная погрешность приближенного числа
∆ = /∆а/ ∆ = /А-а/
Т.к. точное число А обычно неизвестно, то используют верхнюю оценку ∆ – предельную абсолютную погрешность ∆а, т.е. всякое число, не меньше абсолютной погрешности этого числа.
∆ = /А – а/ ≤ ∆а (1)
Т.о. а – ∆а ≤ А ≤ а +∆а
Или А = а ± ∆а
Пример: определить ∆а числа а = 3,14, заменяющего π. Решение: 3,14 < π < 3,15 /а – π/ < 0,01 т.о. ∆а = 0,01 Если учесть, что 3,14 < π < 3,142, то ∆а = 0,02
Нужно выбирать нижнюю грань числа ∆а, удовлетворяющего неравенству (1).
Относительной погрешностью δ приближенного числа а называют отношение абсолютной погрешности ∆ к модулю точного числа А (А ≠0)
δ =
т.е. ∆ = /А/ • δ
Предельной относительной погрешностью δа называется всякое число, не меньшее относительной погрешности приближенного числа а.
δ ≤ δа т.е.
Сравнивая с (1) получаем: предельная абсолютная погрешность равная предельной относительной погрешности умноженной на модуль точного значения числа.
∆а = /А/ • δа (3)
На практике считают (т.к. А ≈ а)
∆а = /а/ • δа (4)
границы для точного числа А равны
а(1 – δа) и а(1 + δа)
т.о. А = а(1 ± δа) 3. Значащая цифра. Число верных знаков.
Примеры:
незначащие цифры
значащие цифры
Т.о. для числа
а = αm • 10m +…+ αm-n+1 – 10m-n +1 +…
(ли известно, что ∆ = /А – а/ ≤ 1/2 • 10m-n +1)
Пример: А = 35,97 а = 36,00 В а верны три знака, т.к. /А – а/ = 0,03 < 1/2 • 0,1 следовательно, 0 • 10-1 – верная значащая цифра.
4. Округление чисел. Чтобы округлить число до n значащих цифр, отбрасывают все цифры его, стоящие справа от n-ой значащей цифры, или, если это нужно для сохранения разряда, заменяют их нулями. При этом: 1) если первая из отброшенных цифр < 5, то оставшиеся десятичные знаки сохраняются без изменения; 2) если первая из отброшенных цифр > 5, то к последней оставшейся цифре добавляется 1; 3) если первая из отброшенных цифр = 5 и среди отброшенных цифр есть ненулевые, то последняя оставшееся цифра увеличивается на 1; 4) если все отброшенные цифры (первая = 5) – нулевые, то последняя оставшееся цифра остается неизменной, если она четная, и увеличивается на 1, если она нечетная.
Рекомендации для практического применения:
1. Количество верных знаков числа отсчитывается от 1-ой значащей цифры числа до первой значащей цифры его абсолютной погрешности. S = 20.7426; ∆s = 0.0926 верные знаки 2, 0, 7. по определению 2, верные значащие цифры были бы 2,0, т.к. 0,09> 1/2 • 0,1 = 0,05 2. В окончательных результатах вычислений обычно оставляют, кроме верных, один сомнительный знак. В промежуточных результатах обычно оставляют два-три сомнительных знака, чтобы не накапливать погрешности от округлений.
Пример: Длина и ширина комнаты, измеренные с точностью до 1 см., равны а = 5,43м; в = 3,82м. Оценить погрешность площади. S = ав = 20,7426 м2 Решение: ∆а = 0,01м; ∆в = 0,01м Smax = (a + 0.01)(в + 0,01) = 20,8952 м2 /Smax – S/ = 0,0926 Smin = (a - 0.01)(в - 0,01) = 20,6502 м2 /Smin – S/ = 0,0924 ∆S = 0,0926. Можно положить ∆S = 0,1. Погрешность увеличивают при округлении. Приближенное значение S = 20,7 (или даже 21).
5. Сложение и вычитание приближенных чисел. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых: если S = а1+а2+…±аn
то ∆S = ∆а1+∆а2+…±∆аn
За предельную абсолютную погрешность можно принять сумму предельных абсолютных погрешностей. Практическое правило для сложения приближенных чисел. 1. выделить числа, десятичная запись которых обрывается ранее других, и оставить их без изменения; 2. остальные числа округлить по образцу выделенных, сохраняя один или два запасных знака; 3. произвести сложение, учитывая все сохраненные знаки; 4. результат округлить на 1 знак
Пример: найти сумму приближенных чисел, каждое из которых имеет все верные значащие цифры: 0,348; 0,1834; 345,4; 235,2; 11,2; 11,75; 9,27; 0,0849; 0,0214; 0,000354. Решение:1) выделяем числа наименьшей точности: 345,4; 235,2 (абсолютная погрешность может достигать 0,1). 2) округляем остальные числа до 0,01 получим
Абсолютная погрешность находится в (приближенно) как сумма абсолютных погрешностей исходных данных и погрешности округления ∆S = 0,10 + 0,05 = 0,15 ∆а = 0,2
Относительная погрешность δs суммы нескольких чисел одного и того же знака между наименьшей и наибольшей из относительных погрешностей слагаемых: min δак ≤ δs ≤ δак (ак > 0, к = 1, 2, 3…, n) Пример: оценить относительную погрешность суммы, найденной в предыдущем примере, и сравнить ее с относительными погрешностями слагаемых. Решение: абсолютная погрешность (погрешность суммирования) ∆ равна 0,1. относительная погрешность δ = ∆/А: Δ = 0,1/602,2 = 0,017 % Относительные погрешности слагаемых: 0,0005/0,348 = 0,5/348 = 15 %
0,5/348 = 15 %; 0,5/1834 = 0,027 %; 0,5/3454 = 0,015 % 05/2352 = 0,022 %; 0,5/1175 = 0,043 %; 0,5/927 = 0,054 % 0,5/849 = 0,059 %; 0,5/214 = 0,24 %; 0,5/354 = 0,015 %
min δак = 0,015 % max δак = 0,24 % δs = 0,017 %
Наибольший вклад в сумму вносят слагаемые 345,4 (δ = 0,015 %) и 235,2 (δ = 0,022 %). δ заключена между этими значениями.
Относительная погрешность разности двух положительных чисел больше относительных погрешностей этих чисел, особенно, если эти числа близки между собой. Это приводит к потере точности при вычитании близких чисел. При приближенных вычислениях полезно преобразовать выражения, связанные с вычислением близких чисел. Пример: U =
U = 0,00353 = 3,53•10–3 вычисления нужно вести с 6 знаками после запятой, т.е. 7 верных знаков.
Преобразуем U:
Заданную точность можно обеспечить, взяв корни лишь с тремя верными знаками. U =
ЛЕКЦИЯ 2 ЛЕКЦИЯ 3 ЛЕКЦИЯ 4
Метод итераций Рассмотрим систему линейных алгебраических уравнений
Если все диагональные элементы
где
Введем обозначения
Тогда система (2) запишется в виде
В качестве начального приближения
.........
Если существует предел x последовательности векторов
Достаточное условие сходимости итерационного процесса: Теорема. Если какая-нибудь норма матрицы А меньше единицы: Под нормой матрицы
Пример: для матрицы
В расчетах полагают
где
Из неравенства (5) можно получить оценку числа итераций k, необходимых для обеспечения заданной точности e. Отклонение приближения
Для вывода (6) достаточно рассмотреть равенства:
Далее И, учитывая, что В неравенствах (5) и (6) используются согласованные нормы для матриц и векторов, т.е. m и l-нормы. Неравенство (6) дает завышенную оценку числа итераций k. Из (6) можно получить удобное условие, позволяющее принять приближение
Пример: Найти решение системы уравнений
методом итераций с точностью 10-2. Решение: Приведем систему к виду (2)
Запишем последовательность итераций
Для приведенной матрицы В качестве начального приближения возьмем вектор-столбец свободных членов приведенной системы Число итераций для достижения заданной точности
Вычислим теперь три последовательных приближения по формулам (8) и оценим погрешность каждого результата, используя неравенство (6) в виде:
Первое приближение:
Следовательно, Далее последовательно находим:
Третья итерация:
Заданная точность достигается за 5 шагов. Точное решение ЛЕКЦИЯ 5 Основные понятия алгебры матриц и теории линейных векторных пространств. 1. Обратная матрица Решение системы линейных уравнений
находится как
где А-1-матрица, обратная к А Обратной матрицей к данной называется матрица, которая, будучи умноженная как справа, так и слева на единичную матрицу, дает единичную матрицу
Нахождение обратной матрицы для данной называется обращением данной матрицы. Квадратной матрицей называется неособенной, если ее определитель отличен от нуля. В противном случае – особенная или сингулярная. Теорема: Всякая неособенная матрица имеет обратную матрицу. Доказательство:Пусть дана неособенная матрица А
Определитель или детерминант квадратной матрицы А
где сумма (4) распространена на всевозможные постановки (α1,α2,…αn) элементов 1,2,3…n и, следовательно, содержит n! Слагаемых, причем n=0, если перестановка четная и n=1, если перестановка нечетная. Перестановка называется четной, если четно число встречающихся в ней инверсий (Инверсия перестановки: когда αi<αj, при i >j) Составим для матрицы А присоединенную матрицу
Где Аij – алгебраическое дополнение (миноры со знаками) соответствующих элементов aij(i,j=1,2,3…n) В присоединенной матрице алгебраические дополнения строк помещаются в соответствующих столбцах, то есть производится операция транспонирования. Обратная матрица А*=А-1 равна Для данной матрицы А ее обратная матрица А-1 (если она существует) – единственная. Теорема: Особенная обратная матрица обратной не имеет. Доказательство:
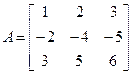
Если А-особенная матрица, то det A=0, Отсюда следует, что 0=1 Теорема доказана. Пример: Для матрицы А найти обратную
Решение:
Составляем присоединенную матрицу:
Свойства обратной матрицы: 1. Определитель обратной матрицы равен обратной величине определителя исходной матрицы
2. Обратная матрица произведения квадратных матриц равна произведению обратных матриц сомножителей, взятому в обратном порядке.
3. Транспонированная обратная матрица равна обратной ей транспонированной данной матрицы
2. Ранг матрицы Определение: Рангом матрицы называется максимальный порядок минора матрица, отличный от нуля. Матрица А имеет ранг r, если:
Разность между наименьшим из чисел m и n (матрица А имеет размерность mxn) и рангом матрицы r называется дефектом матрицы. Если дефект матрицы равен нулю, то ранг матрицы – наибольший из возможных для данной матрицы. Правило нахождения ранга матрицы:
Пример: Найти ранг матрицы А (4х5)
В матрице содержатся миноры второго порядка, отличные от нуля, например:
Окаймляющий его минор третьего порядка:
Оба минора четвертого порядка, окаймляющие минор
Таким образом, r=3, дефект равен 1: m-r=1. 3. Клеточные матрицы Разобьем исходную матрицу на блоки или клетки, или подматрицы
Тогда
Теорема Если непрерывная функция f(x) принимает значение разных знаков на концах отрезков [a, b], то есть Процесс нахождения корней Определяем знаки функции f(x) в ряде точек из области определения функции х1,х2,х3,…, выбор которых учитывается особенностью функции f(x). если окажется, что Пример: Определить действительные корни уравнения:
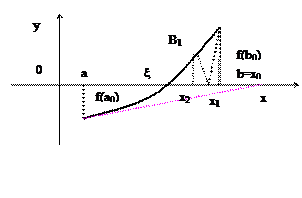
На отрезке [2,3] имеется корень уравнения, так как Для отделения корней можно использовать графические методы. Метод хорд
За приближенное значение корня принимаем точку пересечения с осью ОХ хорды, проходящей через точки A0[a0, f(a0) ], B0[b0, f(b0) ] Уравнение хорды:
Точка пересечения a1 с осью ОХ находится из (1) при у=0 (при этом х=а1):
Принимая а1 за конец первого отрезка
И так далее
Можно показать, что процесс сходится и в пределе Метод Ньютона Пусть ξ – корень уравнения f(x)=0 определен на отрезке Положим Где hn-малая величина. По формуле Тейлора, беря только линейные члены находим:
Так как Из (2) следует:
Подставляя hn в (1), получаем новое приближение корня:
Так как уравнение касательной в точке Bn[bn, f(bn) ]:
Полагая у=0 (корень!); xn=xn+1 получим
Поэтому метод Ньютона называют еще методом касательных. Если в качестве начального приближения выбрать точку а, то получили бы новое приближение, выходящее за интервал
Для оценки точности (погрешности) n-го приближения xn можно воспользоваться следующим соотношением:
Пример: Вычислить методом Ньютона отрицательный корень уравнения:
с пятью верными знаками. Решение: Полагая х=0,-10,-100,…, получим f(0)=-10000, f(-10)=-1050, f(-100)≈108 Искомый корень находится в интервале [-100,-10]. Сузим интервал, рассматривая точку х=-11 f (-11)=3453. Таким образом -11<ξ<-10 На этом интервале Результаты вычислений сводим в таблицу:
Останавливаемся на n=3. проверяем точность решения, давая приращение -5 значащих цифр.
-10261<ξ<-10260 Любое из этих чисел дает искомое приближение. (А хорошо бы еще 1-2 итерации выполнить) ЛЕКЦИЯ 7 Приближенное решение алгебраических и трансцендентных уравнений (продолжение) Метод итераций (метод последовательных приближений) Пусть дано уравнение: f(x)=0 (1) где f(x) – непрерывная функция. требуется вычислить действительный корень уравнения (1) находящийся на отрезке Заменим уравнение (1) на равносильным ему уравнением
где Выбираем произвольное
Аналогично получаем
Рассмотрим последовательность x0,x1,x2,…,xn,… Пусть эта последовательность сходится, то есть существует предел Так как уравнения (1) и (2) равносильны, то c-корень и уравнения (1), то есть исходного уравнения. Выясним при каких значениях процесс сходится. Теорема Пусть функция
Тогда итерационный процесс сходится и дает в пределе единственный корень уравнения Доказательство: Уравнение Выбираем произвольные Рассмотрим уравнение
Т.к. ( Применяем теорему Лагранжа к уравнению (*).
где Согласно неравенству (3), имеем
Аналогично находим
Используя следующее неравенство, получаем
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.100.180 (0.339 с.) |
 и т.д. могут быть представлены лишь приближенно;
и т.д. могут быть представлены лишь приближенно;
 ;
; 

 ; ∆1 = 0,014 /∆1 / = 0,014
; ∆1 = 0,014 /∆1 / = 0,014 ∆2 = -0,0024 /∆2 / = 0,0024
∆2 = -0,0024 /∆2 / = 0,0024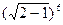
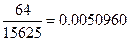




 очевидно абсурден. Сразу не ясно, какой из оставшихся результатов ближе к верному.
очевидно абсурден. Сразу не ясно, какой из оставшихся результатов ближе к верному.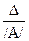 (2)
(2)





 0,00
0,00
 ; найти разность с тремя верными знаками.
; найти разность с тремя верными знаками. = 1,41774469
= 1,41774469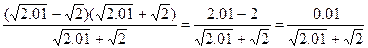

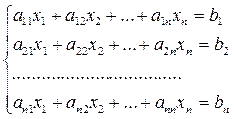 (1)
(1)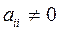
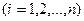 , то систему (1) можно представить в приведенном виде
, то систему (1) можно представить в приведенном виде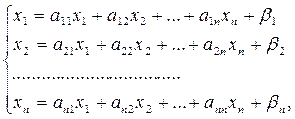 (2)
(2)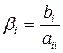
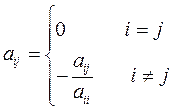
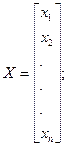
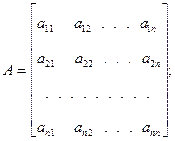
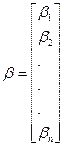
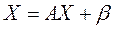 (3)
(3)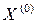 возьмем вектор b и подставим его в уравнение (3). Получим
возьмем вектор b и подставим его в уравнение (3). Получим 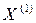 .Продолжая процесс, получим последовательности приближений:
.Продолжая процесс, получим последовательности приближений: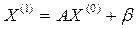 - первое приближение
- первое приближение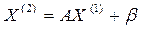 -второе приближение (4)
-второе приближение (4)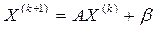 - (k+1)-ое приближение.
- (k+1)-ое приближение.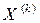 то, переходя к пределу в равенстве
то, переходя к пределу в равенстве 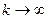 , убеждаемся, что x является решением уравнения (3), т.е.
, убеждаемся, что x является решением уравнения (3), т.е.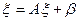
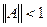 , то уравнение (3) имеет единственное решение x, к которому стремится последовательность итераций (4) при любом выборе начального приближения.
, то уравнение (3) имеет единственное решение x, к которому стремится последовательность итераций (4) при любом выборе начального приближения.
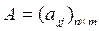 понимают следующие выражения:
понимают следующие выражения: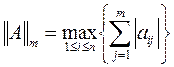 (m – норма - максимальное значение суммы модулей элементов строки)
(m – норма - максимальное значение суммы модулей элементов строки) (l – норма - максимальное значение суммы модулей элементов столбца)
(l – норма - максимальное значение суммы модулей элементов столбца) (k - норма)
(k - норма)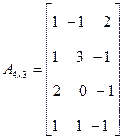
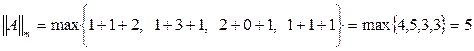
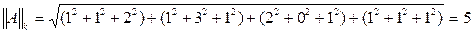
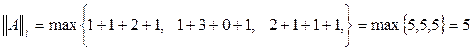
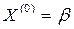 . Погрешности приближенного решения уравнения (3) на k-м шаге оценивают неравенством
. Погрешности приближенного решения уравнения (3) на k-м шаге оценивают неравенством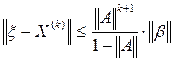 , (5)
, (5)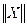 - норма вектора X
- норма вектора X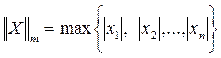 m-норма или кубическая норма
m-норма или кубическая норма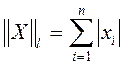 l-норма или октаэдрическая норма
l-норма или октаэдрическая норма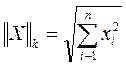 k-норма или сферическая норма.
k-норма или сферическая норма.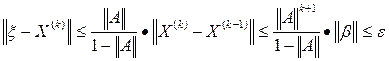 (6)
(6)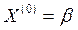 ;
; 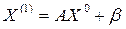 ;
; 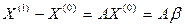 ;
;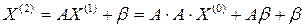 ;
;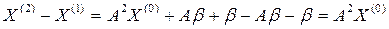 ; и т.д.
; и т.д.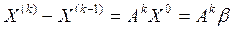
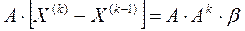 .
.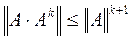 , т.к. норма
, т.к. норма 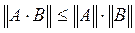 .
.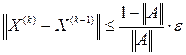 (7)
(7)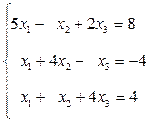
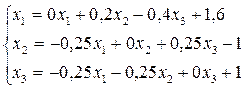
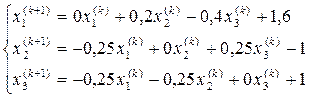 (8)
(8)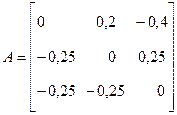 достаточное условие сходимости выполняется по m-норме:
достаточное условие сходимости выполняется по m-норме: 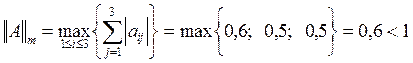
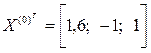 .
.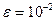 определяем из неравенства (6)
определяем из неравенства (6) 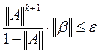 , которое запишем так:
, которое запишем так: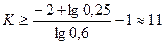 , действительно:
, действительно: 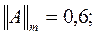
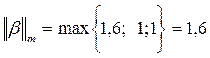 .
.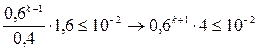 ;
; 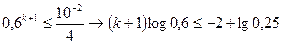 т.к.
т.к. 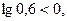 то
то 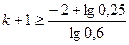 ;
; 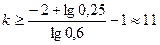 .
.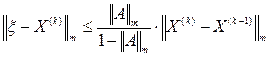 .
. 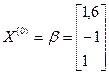
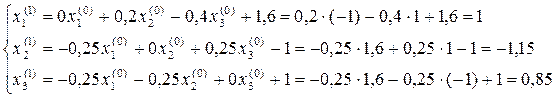
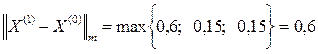
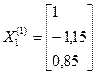 дает значение корня ξ с погрешностью, не превышающей величины
дает значение корня ξ с погрешностью, не превышающей величины 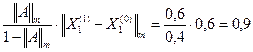 .
.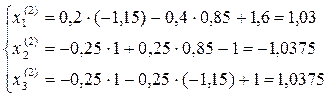
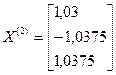 ;
; 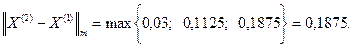
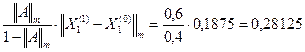 .
.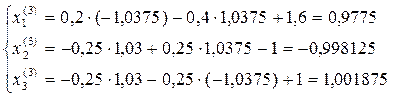
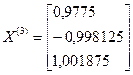 ;
; 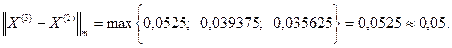
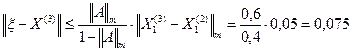 .
.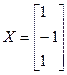 .
.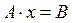 (1)
(1)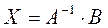 (2)
(2) (3)
(3)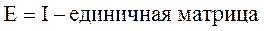
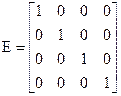
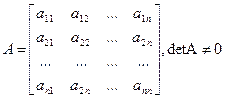
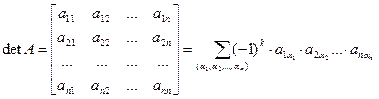 (4)
(4)

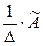 , где Δ – определитель
, где Δ – определитель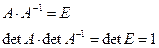

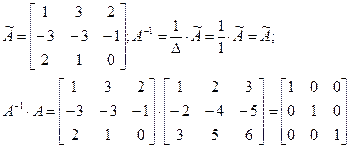

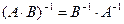

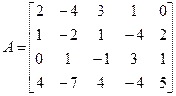

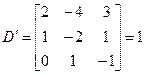
 , равны нулю.
, равны нулю.


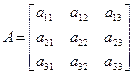 Клетки:
Клетки: 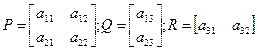

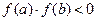 , то внутри этого отрезка находится по крайней мере один корень уравнения f(x)=0. если производная
, то внутри этого отрезка находится по крайней мере один корень уравнения f(x)=0. если производная 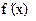 сохраняет свой знак на отрезке [a, b], то корень будет единственный.
сохраняет свой знак на отрезке [a, b], то корень будет единственный.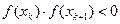 , то на отрезке [xk,xk+1], то имеется по крайней мере один корень уравнения f(x)=0. Необходимо каким-либо способом проверить, является ли этот корень единственным.
, то на отрезке [xk,xk+1], то имеется по крайней мере один корень уравнения f(x)=0. Необходимо каким-либо способом проверить, является ли этот корень единственным.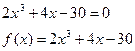
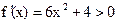 при всех х, то этот корень единственный.
при всех х, то этот корень единственный.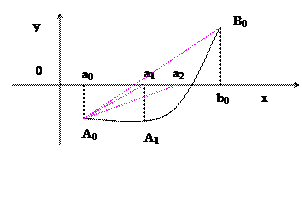 Дано уравнение f(x)=0. Пусть найден отрезок
Дано уравнение f(x)=0. Пусть найден отрезок 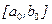 , такой, что на его концах функция f(x) имеет разные знаки, то есть
, такой, что на его концах функция f(x) имеет разные знаки, то есть 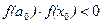 . Пусть, кроме этого, производные
. Пусть, кроме этого, производные 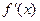 и
и 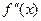 на отрезке
на отрезке 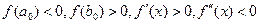 при a0<x<b0).
при a0<x<b0).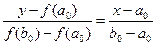 (1)
(1)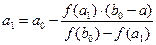 (2)
(2) (3)
(3)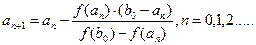 (4)
(4)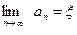 .
.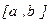 причем
причем 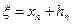 (1)
(1)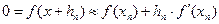 (2)
(2)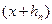 - «корень», то
- «корень», то 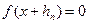
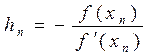
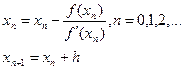 (3)
(3)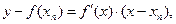
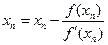
 (4)
(4)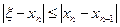 ,
,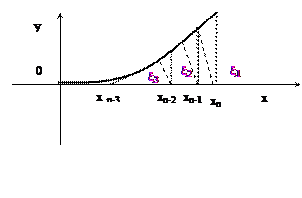 То есть «установившееся» начальные десятичные знаки приближения xn и xn+1,являются верными (следует взять более двух последующих приближений!)
То есть «установившееся» начальные десятичные знаки приближения xn и xn+1,являются верными (следует взять более двух последующих приближений!)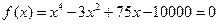
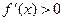 и
и 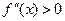 . Так как
. Так как 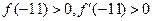 , то есть
, то есть 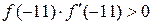 , за начальное приближение выбираем х0=-11.
, за начальное приближение выбираем х0=-11.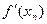
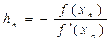
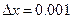 . (два знака до запятой, три знака – после)
. (два знака до запятой, три знака – после)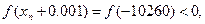
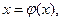 (2)
(2)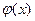 - непрерывна на
- непрерывна на  и подставляем его в правую часть равенства (2). Получаем
и подставляем его в правую часть равенства (2). Получаем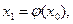
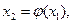
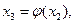
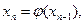
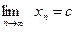 . Покажем, что с – корень уравнения (2) По построению
. Покажем, что с – корень уравнения (2) По построению 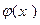 - непрерывная функция. Переходя к пределу при
- непрерывная функция. Переходя к пределу при 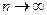 , получаем
, получаем 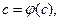 что и требовалось доказать.
что и требовалось доказать.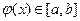 . Пусть кроме этого,
. Пусть кроме этого,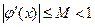 при
при 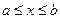 (3)
(3)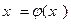
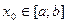 и строим итерационную последовательность
и строим итерационную последовательность 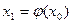 ;
; 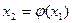 ;…;
;…; 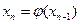 .
.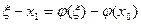 . (*)
. (*)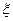 - корень уравнения
- корень уравнения 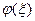 , т.е.
, т.е. 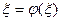 , а
, а 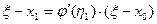 ,
,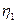 лежит между
лежит между 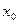 , т.е.
, т.е. 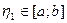 .
.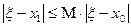 , т.к.
, т.к. 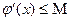 .
.