
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
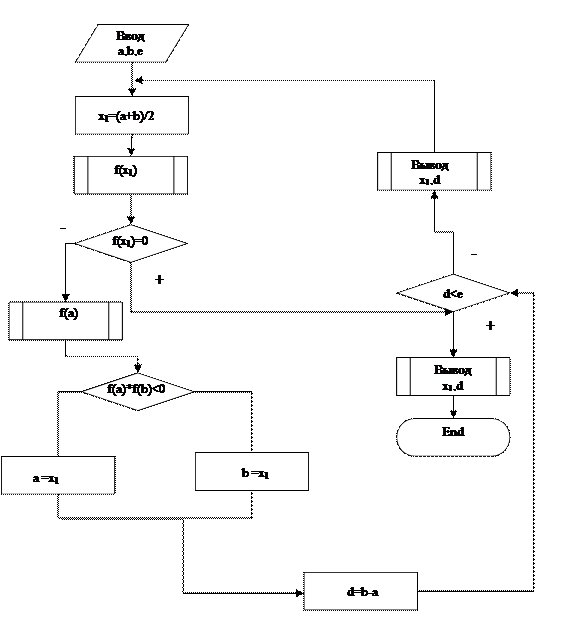
Блок – схема решения уравнения f(x) методом половинного деленияСодержание книги
Поиск на нашем сайте
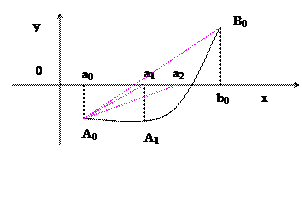
Метод хорд
За приближенное значение корня принимаем точку пересечения с осью ОХ хорды, проходящей через точки A0[a0, f(a0) ], B0[b0, f(b0) ] Уравнение хорды:
Точка пересечения a1 с осью ОХ находится из (1) при у=0 (при этом х=а1):
Принимая а1 за конец первого отрезка
И так далее
Можно показать, что процесс сходится и в пределе Метод Ньютона Пусть ξ – корень уравнения f(x)=0 определен на отрезке Положим Где hn-малая величина. По формуле Тейлора, беря только линейные члены находим:
Так как Из (2) следует:
Подставляя hn в (1), получаем новое приближение корня:
Так как уравнение касательной в точке Bn[bn, f(bn) ]:
Полагая у=0 (корень!); xn=xn+1 получим
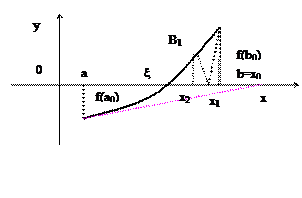
Поэтому метод Ньютона называют еще методом касательных. Если в качестве начального приближения выбрать точку а, то получили бы новое приближение, выходящее за интервал
Для оценки точности (погрешности) n-го приближения xn можно воспользоваться следующим соотношением:
Пример: Вычислить методом Ньютона отрицательный корень уравнения:
с пятью верными знаками. Решение: Полагая х=0,-10,-100,…, получим f(0)=-10000, f(-10)=-1050, f(-100)≈108 Искомый корень находится в интервале [-100,-10]. Сузим интервал, рассматривая точку х=-11 f (-11)=3453. Таким образом -11<ξ<-10 На этом интервале Результаты вычислений сводим в таблицу:
Останавливаемся на n=3. проверяем точность решения, давая приращение -5 значащих цифр.
-10261<ξ<-10260 Любое из этих чисел дает искомое приближение. (А хорошо бы еще 1-2 итерации выполнить) ЛЕКЦИЯ 7 Приближенное решение алгебраических и трансцендентных уравнений (продолжение) Метод итераций (метод последовательных приближений) Пусть дано уравнение: f(x)=0 (1) где f(x) – непрерывная функция. требуется вычислить действительный корень уравнения (1) находящийся на отрезке Заменим уравнение (1) на равносильным ему уравнением
где Выбираем произвольное
Аналогично получаем
Рассмотрим последовательность x0,x1,x2,…,xn,… Пусть эта последовательность сходится, то есть существует предел Так как уравнения (1) и (2) равносильны, то c-корень и уравнения (1), то есть исходного уравнения. Выясним при каких значениях процесс сходится. Теорема Пусть функция
Тогда итерационный процесс сходится и дает в пределе единственный корень уравнения Доказательство: Уравнение Выбираем произвольные Рассмотрим уравнение
Т.к. ( Применяем теорему Лагранжа к уравнению (*).
где Согласно неравенству (3), имеем
Аналогично находим
Используя следующее неравенство, получаем
Повторяя процесс, получаем
По условию теоремы
Т.е. итерационная последовательность сходится и дает в пределе корень уравнения Действительно, предположим, что на этом отрезке есть еще корень уравнения Пришли к противоречию. Теорема доказана. Замечание 1. По условию теоремы итерационный процесс сходится при любом выборе Замечание 2. Т.к.
Геометрический смысл метода итераций.
а) При
Условие теоремы
б) При
в) При
Для применения метода итераций уравнение Это можно сделать различными способами: 1. Уравнение В этом случае Параметр подбирают так, чтобы 2. Уравнение где
Можно показать, что при соответствующем выборе функции
Оценка приближения. Из условия (4) Приведем без доказательства еще одну формулу для оценки погрешностей. Из (1) и (2) следует, что итерационный процесс сходится тем быстрее, чем меньше Если Если за приближенное значение корня взять полусумму последних полученных приближений Пример: Вычислить приближенно действительный корень уравнения.
Вычислим
получаем Находим Пусть Тогда
При Получаем Пусть При таком Выбираем Подставляем
получаем Аналогично находим:
Оценим погрешность по формуле
Итак
1) Условие сходимости 2) Если производная
ЛЕКЦИЯ 8 Интерполирование функций.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.54.147 (0.007 с.) |

 Дано уравнение f(x)=0. Пусть найден отрезок
Дано уравнение f(x)=0. Пусть найден отрезок 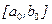 , такой, что на его концах функция f(x) имеет разные знаки, то есть
, такой, что на его концах функция f(x) имеет разные знаки, то есть 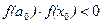 . Пусть, кроме этого, производные
. Пусть, кроме этого, производные 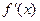 и
и 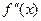 на отрезке
на отрезке 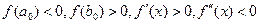 при a0<x<b0).
при a0<x<b0).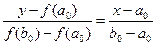 (1)
(1)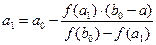 (2)
(2) (3)
(3)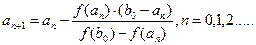 (4)
(4)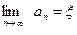 .
.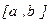 причем
причем 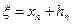 (1)
(1)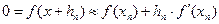 (2)
(2)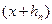 - «корень», то
- «корень», то 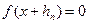
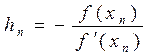
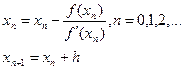 (3)
(3)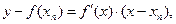
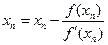
 (4)
(4)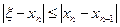 ,
,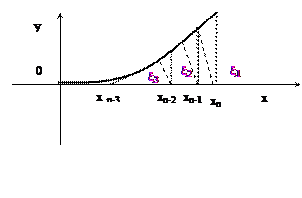 То есть «установившееся» начальные десятичные знаки приближения xn и xn+1,являются верными (следует взять более двух последующих приближений!)
То есть «установившееся» начальные десятичные знаки приближения xn и xn+1,являются верными (следует взять более двух последующих приближений!)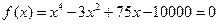
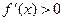 и
и 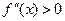 . Так как
. Так как 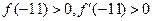 , то есть
, то есть 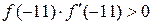 , за начальное приближение выбираем х0=-11.
, за начальное приближение выбираем х0=-11.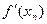
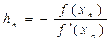
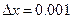 . (два знака до запятой, три знака – после)
. (два знака до запятой, три знака – после)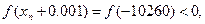
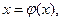 (2)
(2)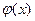 - непрерывна на
- непрерывна на  и подставляем его в правую часть равенства (2). Получаем
и подставляем его в правую часть равенства (2). Получаем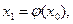
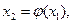
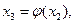
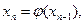
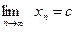 . Покажем, что с – корень уравнения (2) По построению
. Покажем, что с – корень уравнения (2) По построению 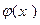 - непрерывная функция. Переходя к пределу при
- непрерывная функция. Переходя к пределу при 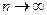 , получаем
, получаем 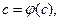 что и требовалось доказать.
что и требовалось доказать.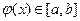 . Пусть кроме этого,
. Пусть кроме этого,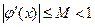 при
при 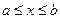 (3)
(3)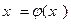
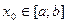 и строим итерационную последовательность
и строим итерационную последовательность 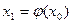 ;
; 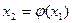 ;…;
;…; 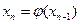 .
.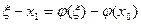 . (*)
. (*)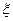 - корень уравнения
- корень уравнения 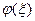 , т.е.
, т.е. 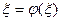 , а
, а 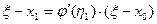 ,
,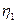 лежит между
лежит между 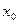 , т.е.
, т.е. 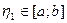 .
.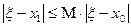 , т.к.
, т.к. 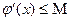 .
.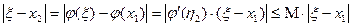
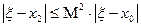
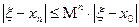 (4)
(4)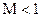 , поэтому из (4) следует
, поэтому из (4) следует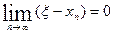 , т.е.
, т.е. 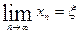 .
.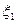 . Тогда
. Тогда 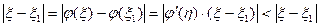 т.к.
т.к. 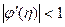 .
.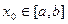 . Благодаря этому он является самоисправляющимся, т.к. неверно вычисленное
. Благодаря этому он является самоисправляющимся, т.к. неверно вычисленное 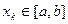 можно рассматривать как новое нулевое приближение.
можно рассматривать как новое нулевое приближение.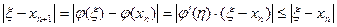 ,
, 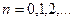
 , то каждое последующее приближение ближе к корню чем предыдущее.
, то каждое последующее приближение ближе к корню чем предыдущее. Корень уравнения
Корень уравнения 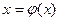 - это абсцисса точки пересечения кривой
- это абсцисса точки пересечения кривой 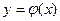 и прямой
и прямой 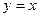 .
.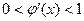 приближения
приближения 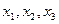 и т.д. монотонно убывают, приближаясь к
и т.д. монотонно убывают, приближаясь к 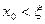 ).
).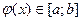 , автоматически выполняются если
, автоматически выполняются если 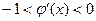 последовательные приближения колеблются около
последовательные приближения колеблются около 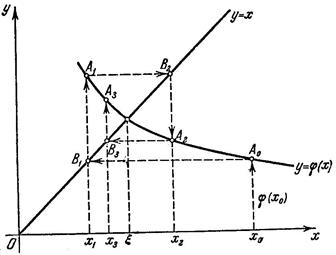
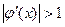 итерационный процесс расходится!
итерационный процесс расходится!
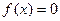 нужно привести к виду
нужно привести к виду 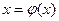 так, чтобы
так, чтобы 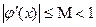 при
при 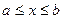 .
.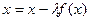 .
.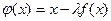 .
.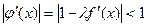 , при
, при 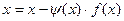 ,
,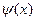 - произвольная, дифференцируемая на отрезке
- произвольная, дифференцируемая на отрезке 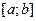 функция, не имеющая корней на отрезке
функция, не имеющая корней на отрезке 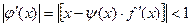 , при
, при 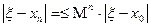 , учитывая, что
, учитывая, что 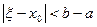 , получаем
, получаем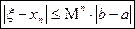 . (1)
. (1)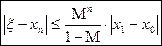 . (2)
. (2)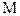 .
.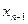 и
и 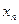 , в этом случае лежат по разные стороны от корня
, в этом случае лежат по разные стороны от корня 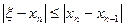 . (3)
. (3)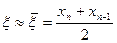 , то
, то 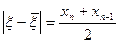 .
.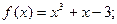
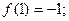
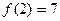 .
.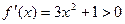 при всех
при всех 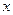 .
. Сузим этот интервал методом половинного деления.
Сузим этот интервал методом половинного деления.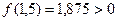 , поэтому
, поэтому 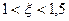 .
.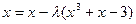 ,
,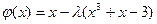 ;
; 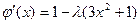 .
.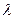 , такое чтобы
, такое чтобы 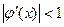 при
при 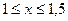 .
.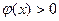
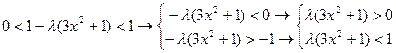
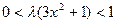
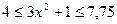
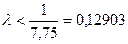 .
.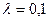
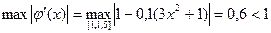 ;
; 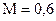 .
.
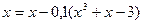
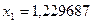
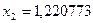 ;
; 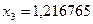 ;
; 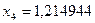 ;
; 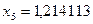 ;
; 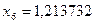 ;
; 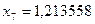 ;
; 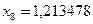 ;
; 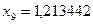 ;
;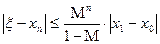
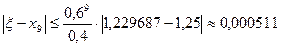
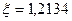 ;
; 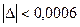
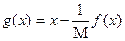 , где
, где 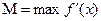
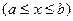 .
.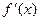 отрицательна на отрезке
отрицательна на отрезке 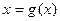 , заменяется на
, заменяется на 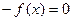 .
.


