
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конечные разности различных порядков.Содержание книги
Поиск на нашем сайте
Пусть
называется первой конечной разностью функции Конечные разности высших порядков
Например,
Пример. Построить конечные разности для функции:
Решение:
Если
где Символ Основные свойства оператора 1) 2) 3) Имеет место важная формула, которая может быть получена на основе свойств 1-3.
где Из (2) следует.
Переходя к пределу и предполагая, что
2) Таблица разностей. Часто таблицы задаются для системы равноотстоящих точек
Конечные разности определяются соотношениями:
В общем виде можно записать:
где Например:
и т.д. Для вычисления n-ой разности Конечные разности различных порядков удобно располагать в форме таблиц двух видов: Горизонтальная таблица разностей. Диагональная таблица разностей.
Пример: Составить горизонтальную таблицу разностей функции
от начального значения Решение: Полагая Отсюда Т.к. n=3 – степень полинома, то 3-и разности Заносим полученные значения в таблицу (горизонтальную).
Исходные данные для заполнения таблицы отмечены ступенчатой ломаной. Остальные клетки можно заполнить с помощью формул
отсюда:
Постановка задачи интерполирования. На отрезке
Требуется построить интерполирующую функцию F(x), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и
В общем случае, задача имеет бесчисленное множество решений!!! Задача становится однозначной, если решение искать в заданном классе функций! Будем искать полином Полученную интерполяционную формулу Если При
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.255.239 (0.005 с.) |

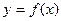 - заданная функция. Обозначим через
- заданная функция. Обозначим через 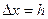 фиксированную величину приращения аргумента (шаг). Тогда выражение
фиксированную величину приращения аргумента (шаг). Тогда выражение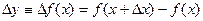 (1)
(1)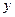 .
.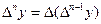
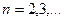
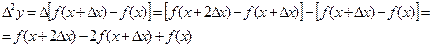
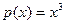 , считая шаг
, считая шаг 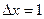 .
.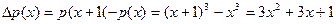 ,
,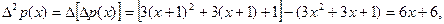
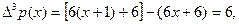
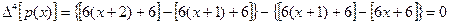 .
.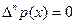 , при
, при 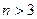 .
.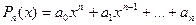 - полином n-ой степени, то
- полином n-ой степени, то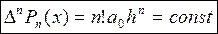 (*)
(*)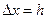 .
. можно рассматривать как оператор, ставящий в соответствие функции
можно рассматривать как оператор, ставящий в соответствие функции  .
.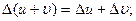
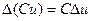 , где
, где 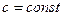 ;
;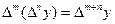 .
.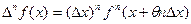 , (2)
, (2)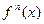 - производная (непрерывная) на отрезке
- производная (непрерывная) на отрезке 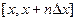 ,
, 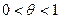 .
.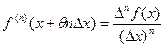
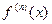 непрерывна, получаем
непрерывна, получаем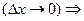
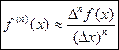 - формула для приближенного вычисления производных.
- формула для приближенного вычисления производных.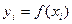
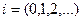
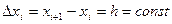 .
.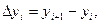
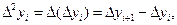
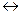 в силу свойства 1):
в силу свойства 1): 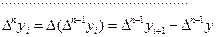
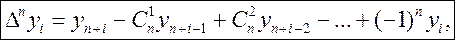 (1)
(1)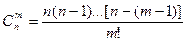 - число сочетаний из n элементов по m.
- число сочетаний из n элементов по m.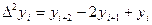 ,
,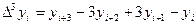 ,
,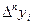 , нужно знать n+1 членов
, нужно знать n+1 членов 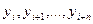 последовательности.
последовательности.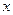
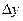
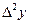
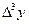
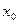
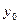
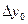
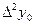
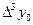
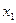
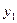
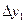
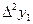
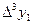
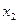
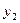
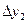
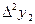
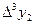
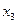
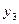
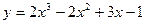
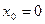 , приняв шаг
, приняв шаг 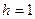 .
.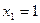 ,
, 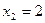 , находим
, находим 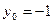 ,
, 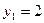 ,
, 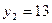 .
.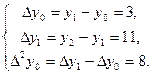
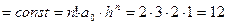 .
.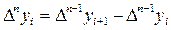
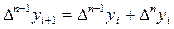
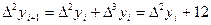 ,
,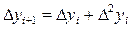 и т.д.
и т.д.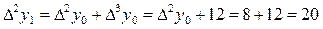 ,
,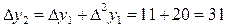 и т.д.
и т.д.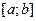 заданы n+1 точки
заданы n+1 точки 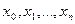 , которые называются узлами интерполяции, и значение некоторой функции
, которые называются узлами интерполяции, и значение некоторой функции 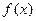 в этих точках
в этих точках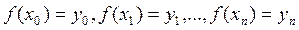 . (1)
. (1)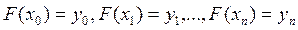 (2)
(2)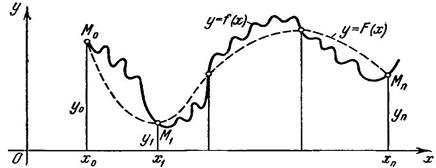
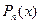 степени не выше n и удовлетворяющий условию (2).
степени не выше n и удовлетворяющий условию (2).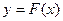 используют для вычисления значений
используют для вычисления значений 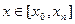 - имеет место задача интерполирования (интерполирование “в узком смысле”).
- имеет место задача интерполирования (интерполирование “в узком смысле”).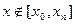 решается задача экстраполирования.
решается задача экстраполирования.


