Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конечно-разностные аппроксимации производных.
Пусть отрезок [а,b] разбит на n (n Производные можно записывать с помощью конечных разностей: а) разностей вперед: в) разностей назад (левые разности): c) центральных разностей: Приближенное значение производной второго порядка в точке хi:
Т.о Погрешность аппроксимации (3) имеет порядок 0 ( 3. Использования интерполяционных многочленов Лагранжа для формул численного дифференцирования. Функция у=f(x) на отрезке [a,b] разбитых на n равных интервалов, принимает значение в точках {xi} (i=0,1,2….k) yi=f(xi); b=xn; h=xi-xi-1=const. Построим интерполяционный многочлен Лагранжа Lm(x) степень M: Lm(x)=f(x k)=y k (k=i,i+1,….,i+m) i+m Многочлен Lm(x) интерполирует функцию f(x) на отрезке [xi,xi+m]. Дифференцируя Lm(x), получаем значение производных в точках {xk} (k=i,i+1,…,i+m). (Можно получить значения и в точках,отличных от узлов.) Если m=1, то L1(x)-линейная функция, график которой проходит через точки (хi,yi) и (хi+1,yi+1). Тогда L1(x)=
Если m=2, то график L2(x) – парабола, проходящая через точки (хi,yi), (хi+1,yi+1), (хi+2,yi+2). L2(x)= L2’(x)=
L2”(x)=
Подставляя в (1) и (2) значения х, равные хi,xi+1,xi+2: Получим приближения производных f’(x) и f”(x) в этоих точках: учитывая, что
Если функция f(x) имеет непрерывную производную до 3-го порядка включительно,то
f(x) = L2(x)+ R2(x), (5) где R2(x)- остаточный член интерполяционной формулы. R2(x)=
Дифференцируя (5),получим f’(x) = L’2(x)+ R’2(x) (6) f”(x) = L”2(x)+ R”2(x) (7)
Здесь, R’2(x)= Т.к. f”’( R”2(x)= В точках хi,xi+1,xi+2 (т.е. в узлах) получаем (подставляя значения хi и т.д. в (8)-(9) и учитывая хi-xi+1=-h): R’2(xi)= R”2(xi)= Т.о. равенства (10) показывают, что погрешность аппроксимации первой производной f’(x) с помощью формулы (3) имеет один и тот же порядок 0(h2). (во всех трех точках.) На отрезке [a,b] в точках хi (i=0,1,2…,n) при n
Погрешность аппроксимации второй производной имеет различный порядок в различных точках.(равенство(11)).Поэтому рекомендуется использовать многочлен Лагранжа третьей степени L3(x), имеющей 4 точки (узла) интерполяции. При этом погрешность во всех точках имеет один порядок h2. Рекомендуется формулы:
Пример: Значение функции y=sin x заданы таблицей
Найти значения Решение: По формулам (3) или (12) получаем:
По формуле (10): Т.к f(x)=sin x, то f”’(x)=-cos x.
По формуле (4)
По формуле (11): Т.о. y’0 y”0=sin0=0
Следовало бы уменьшить шаг и увеличить число шагов. Затем использовать полином Лагранжа 4-ой степени и формулы (13).
Блок-схема вычисления производной.
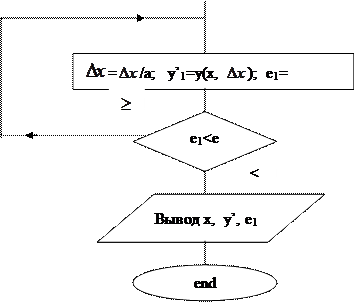
ЛЕКЦИЯ 12 Численное интегрирование. S= Обозначим: Заменим y=f(x) …… кусочно-полиномиальной функцией S(x) аппроксимирующей данную функцию. Интегрируя S(x) на отрезке [a,b], получим формулу численного интегрирования – квадратную формулу. 1)если на каждом интервале [
f(x) где
и получаем квадратурную формулу прямоугольников:
2)Если f(x) на каждом отрезке [
Действительно:
(т.к.
Т.о. получаем квадратурную формулу трапеций:
3) Если …. S(x), определяет собой непрерывную функцию, составленную из примыкающих парабол, можно получить квадратурную формулу Симпсона, или формулу парабол. Пусть на отрезке [ (в знаменателе(первый шаг):
Введем новую переменную t: t = Тогда Значениям t= 0, 1/2, 1 соответствуют значения х,равные
Выразим S(x) через новую переменную t:
S(x)= = Рассмотрим, например, 1-ый член Т.к.
= Далее, учитывая, что
Т.о. имеем квадратурную формулу парабол:
Погрешность каждой квадратичной формулы оценивается величиной остаточного члена R(h), зависящего от шага разбиения h (или от числа разбиений n):
Если f(x) имеет непрерывную производную второго порядка, то получаем: Для формулы трапеций
Если f(x) имеет непрерывную производную 4-го порядка, то оценка погрешности формулы Симпсона:
Пример: Найти приближенное значение интеграла Решение: Погрешность Находим производные f(x):
При n=4 получим:
Результаты сведены в таблицу:
Метод двойного пересчета Позволяет оценить текущую оценку точности 1.проводится вычисления с шагом h и получается 2.шаг h уменьшается вдвое и получается 3.используется правило Рунге:
K=2 –прямоугольников и трапеции К=4- для формулы Симпсона При заданной точности при этом полагают
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.39.23 (0.053 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 2) равных частей.
2) равных частей.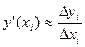 ;
; 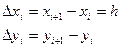
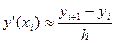 (i=0,1,….,n-1) (1)
(i=0,1,….,n-1) (1)  ;
; 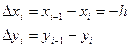 (2)
(2)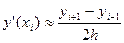 ;
; 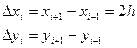
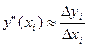 ,
, 
 ;
; 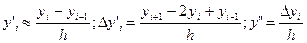
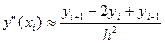 i=1,2,…..n-1 (3)
i=1,2,…..n-1 (3)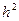 ).
). n.
n.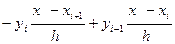 ; L1’(x)=
; L1’(x)= 
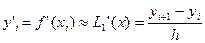

 (1)
(1)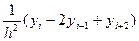 (2)
(2) ;
; 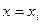


 (3)
(3)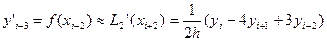
 (4)
(4)
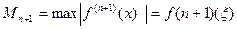 ;
; 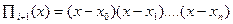
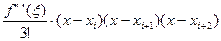
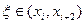
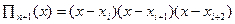
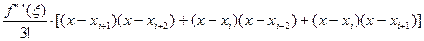 ;
; 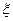 )=const –дифференцируем по х.
)=const –дифференцируем по х.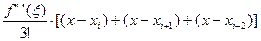 ;
;  (10)
(10) ,
,  ,
,  =
=  (11)
(11)  i=0;
i=0;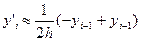 (i=1,2,…,n-1); (12)
(i=1,2,…,n-1); (12) i=n;
i=n;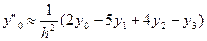 i=0;
i=0;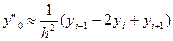 (i=1,2,….,n-1);
(i=1,2,….,n-1);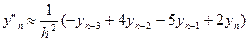 i=n;
i=n;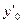 и
и  и оценить погрешности вычислений.
и оценить погрешности вычислений. ;
;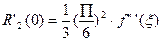 0<
0< 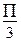
 . Т.о. y’0
. Т.о. y’0  1.05
1.05 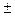 0.09
0.09
 получаем
получаем 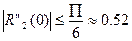



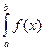 .Разобьем отрезок [a,b] на n равных частей.
.Разобьем отрезок [a,b] на n равных частей. 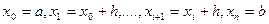
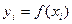
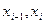 ] (i=1,2,…,n.) заменим f(x) ступенчатой функцией
] (i=1,2,…,n.) заменим f(x) ступенчатой функцией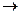 S(x) =
S(x) =  ,
, 
 - середина интервала
- середина интервала 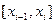
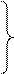 тогда
тогда  т.к
т.к 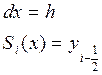
 (1)
(1)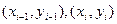 , то получим
, то получим
 i=1,…,n
i=1,…,n 
 i=1,2,…..,n
i=1,2,…..,n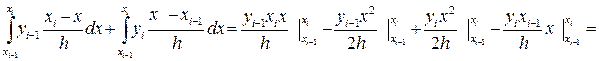
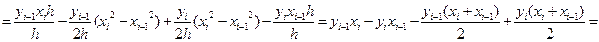
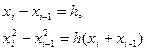 ) =
) = 

 (2)
(2) ),(
),( ),(
),( ). Строим интерполяционный многочлен Лагранжа второго порядка:
). Строим интерполяционный многочлен Лагранжа второго порядка: )
)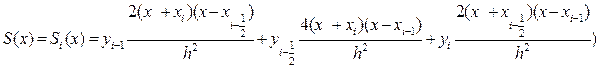
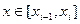 i=1,2,….,n
i=1,2,….,n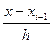 ;
;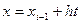 ;
; 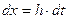 ;
; .
.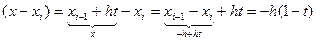 и т.д.
и т.д. =
= (i=1,2,….,n)
(i=1,2,….,n)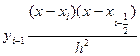
 , а
, а  , получаем:
, получаем: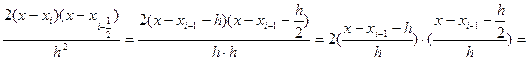

 , получаем:
, получаем: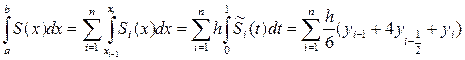
 (3)
(3)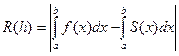

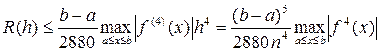
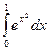 с помощью квадратурных формул прямоугольников, трапеций и Симпсона, если отрезок интегрирования [0,1] разбит на n =2; 4;10 равных частей. Оценить величину погрешности полученных результатов.
с помощью квадратурных формул прямоугольников, трапеций и Симпсона, если отрезок интегрирования [0,1] разбит на n =2; 4;10 равных частей. Оценить величину погрешности полученных результатов. .
.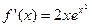 ;
;  ;
;  ;
; 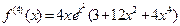
 ;
; 
 ;
;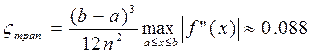
 (в 200 раз точнее)
(в 200 раз точнее)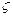
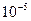
 (h).
(h). , где Y- точное значение интеграла
, где Y- точное значение интеграла