
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия нахождения экстремума функции
Условие минимума: Т. о. условие экстремума дает систему m+1 уравнений m+1 неизвестными
Введем обозначения:
Например: k=1; тогда S1 = х0+ х1+…+ хn t1 = х0y0+ х1 y1+…+ хn yn t0 = х00 y0+ х10 y1+…+ хn0 yn =Σyi S0= х00 + х10 +…+ хn0 =1+1…1 = n+1
Тогда система (3) примет вид:
a0 s0 + a1 s1 + a2 s2 +…+ am sm = t0 a0 s1 + a1 s2 + a2 s3 +…+ am sm+1 = t0 (4) a0 s2 + a1 s3 + a2 s4+…+ am sm+2 = t0 a0 sm + a1 sm+1 + a2 sm+2 +…+ am s2m = t0
где S0 = n+1.
Если среди точек x0, х1,…, хn нет совпадающих и m≤n, то определитель системы (4) отличен от нуля и система имеет единственное решение a0=a0٭,a1=a1٭,…,am=am٭ Полином (1) с таким коэффициентом будет обладать минимальным среднеквадратичным отклонением Smin.
(т.е. будет решаться задача интегрирования) и Smin=0. ,то аппроксимирования функций – более общий процесс, чем интерполирование.
Пример: подобрать аппроксимирующий полином второй степени y = a0+a1x+a2x2 для данных:
m = 2 n = 4 (n+1=5)
Cтроим таблицу
11.61 a0 + 32.768 a1 + 102.761 a2 = 29.770 (5) 32.768 a0 + 102.761 a1 + 341.750 a2 = 94.604
Решая систему (S) получаем: а0=5.045; а1=4.043; а2=1,009. Т.е. у = 5.045 – 4.043 х + 1.009 х2
Сопоставим некоторые значения Yi с вычисляемыми (6)
|ε|max=0.01 Удобнее пользоваться при оценке «качества» приближения не таблицей, а одним показателем – среднеквадратической нормой.
d (f, Qm) = ( Или величиной ∂ (f, Qm) = d (f, Qm)/ ║f║, где ║f║ - норма функции;
║f║ =
В нашем случае: d = Еще более удобный показатель – относительное среднеквадратическое отклонение ∂ ∂(f, Qm) = d (f, Qm)/ ║f║ - безразмерная величина.
В нашем случае ║f║ = ∂(f, Qm) ≈2,6*10-3 = 0,0026
Правильнее было бы называть среднеквадратическим отклонением величину
Мы рассмотрели приближение функции обычным полиномом. Рассмотрим теперь аппроксимацию обобщенным полиномом. Qm (х)=C0φ0 (x)+C1φ1 (x) +...+ Cmφm (x). Теперь необходимо минимизировать сумму квадратов n Sm=Σ [C0φ0 (xі) + C1φ1 (xі) +...+ Cmφm (xі) – f (xі)]2 і=0 Условия экстремума дают систему уравнений
n Введем обозначения: (φ,ψ) = Σ φ (xі) × ψ (xі) і=0 Тогда (7) примет вид:
C0 (φ0, φ1) + C1 (φ1, φ1) +…+ Cm (φm, φ1) = (f, φ1) (8) C0 (φ0, φm) + C1 (φ1, φm) +…+ Cm (φm, φm) = (f, φm)
Из этой системы определяют коэффициенты C0, C1,…, Cm.
ЛЕКЦИЯ 16 . Функции, ортогональные на точечном множестве.
точек x = {x0, x1, x2,…, xn}, если n Σ φ (xі) × ψ (xі) = 0. і=0
Пример: φ (x) = 3x² - 15x + 10; ψ (x) = 2x – 5 ортогональны на множестве xі = і (і = 0,1,2,3,4,5). Имеем: φ (0) = 10;
системы попарно ортогональны между собой на этом множестве X. Функция φ(x)≡0, естественно, ортогональна любой функции. Поэтому будем рассматривать только такие функции,
n Σ φ² (xі) > 0 і=0 т.е. хотя бы одно значение φ (xі) ≠ 0
выполнено равенство ║φk (x)║ = 1, где Если {φk (x)} – система функций ортогональна на множестве Х, то система функций {φk (x) ⁄ ║φk║х} – ортогональная на Х.
В противном случае функции fk (x) – линейно зависимые на Х. Если множество Х не точечное, а континумум, т.е. х принадлежит отрезку a < х < b, то условие линейной независимости то же самое, только рассматриваются не точки xі, а множество х? (a, b), т.е. рассматриваем условие m Σ λkfk (x) = 0 х? (a, b) k=0 Легко можно доказать лемму: Функции φk (x) (k = 0, 1,…,m), ортогональные на множестве Х = {x0, x1, x2,…,xm} и имеющие ненулевые нормы, линейно независимы на этом множестве. Рассмотрим систему полиномов P0 (x), P1 (x),…, Pm (x), (1)
ортогональны на точечном множестве Х = {x0, x1,…,xn}, т.е. n Σ Pі (xі) Pk (xі) = 0 при j ≠ k (2) і=0 2 n 2 и таких, что Sj = ║Pj║ = Σ Pj (xі) > 0 – квадрат нормы x і=0 Пусть степень полинома Pj = j Т.к. полином Pі (x) (j = 0, 1, 2,…,m) линейно независимые на Х поскольку они ортогональны, то любой полином Qm (x) степени не выше m может быть представлен в виде линейной комбинации полиномов (2), т.е. Qm (x) = b0 P0 (x) + b1P1 (x) +…+ bmPm (x) (3),
Выражение (3) называется разложением полинома Qm (x) по системе (1) Если полином Pj (x) ортогональны, то коэффициенты bk равны
Действительно, умножим (3) на полином Pk (x) (k ≤ m) и просуммируем результат по всем xi
n n n n 2 n Σ Qm (xi) × Pk (xi) = b0 Σ P0 (xi) × Pk (xi) + b1 Σ P1 (xi) × Pk (xi) +...+ bk Σ Pk (xi) +...+ bm Σ Pm (xi) × і=0 і=0 і=0 і=0 і=0 × Pk (xi) (5)
В силу условия ортогональности из (5) следует (4), т.к. все Σ Pj (x) × Pk (x) = 0 для j≠k
n Если система (1) ортогональна на Х, т.е. Σ Qm (xi) × Pk (xi) (6) і=0 Теперь будем аппроксимировать заданную функцию y = f (х) полиномом Qm (x) на множестве Х. Qm (x) = C0P0 (x) + C1P1 (x) +…+ CmPm (x),
n 2 Минимизируя S m = Σ [C0P0 (xi) + C1P1 (xi) +…+ CmPm (xi) - f (хi)] по C1, C2,…, Cm, т.е. приравнивая і=0
Ck – коэффициенты Фурье функции f (x) относительно ортогональной системы {Pk (x)} на Х
Беря вторую производную Cm (Ck) – минимальна! Т.о.
Можно показать, что для полинома Фурье 2 m 2 2 Sm = ║f (х)║ - Σ Ck × ║Pk║ k=0 x 2 2 m n Если система {Pk (x)} ортонормирована, то ║Pk║ = 1 и Sm = ║f (х)║ - Σ Ck , Ck = Σ f (хi) × Pk (хi) х k=0 і=0
III. Полиномы Чебышева, ортогональные на системе равноотстоящих точек. Пусть дана система n + 1 равноотстоящих точек х = {x0, x1,…,xn} с шагом n. С помощью линейного преобразования Полиномы P0, n (t), P1, n (t),…, Pm, n (t) (m ≤ n) степеней 0, 1,…, m, ортогональные на множестве {0, 1, 2,…,n} и отличные от нуля на этом множестве, называются ортогональными полиномами Чебышева. (Pk, n (t): k – степень полинома, n – число точек, уменьшенное на 1) Полиномы Чебышева можно задать формулой
k s s s t[ s]____ (1) Pk, n (t) = Σ (-1) C C ×
где k = 0, 1,…, m;
s C - число сочетаний из k по s k
t[s] = t × (t - 1) × (t - 2) ×...× (t-s +1) обобщенные степени t и n n [s] = n × (n - 1) × (n - 2) ×...× (n – s+1) Т.о. четыре первых ортогональных полинома равны:
Возвращаясь к прежней переменной х, получим систему полиномов, ортогональных на множестве Х Можно показать, что квадрат нормы полинома
Разделив многочлены
Пример. Получить систему полиномов до третьей степени включительно, ортонормированных на системе точек Решение. Полагая
(k=0, n=s)
k=1, n=5 s=0 1 2 переходим к Х 1-0,4t=1-0,4* И т.д.
По формуле (3) вычисляем нормы
Делим полиномы
Если функция Y=f(x) задана на множестве узлов
(5)
(k=0,1,2,…,m) (6) Из (5) и (6) следует, что полином Поэтому часто вместо полиномов
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 46; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.65.65 (0.122 с.) |
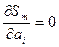

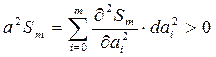 , т.е. второй дифференциал >0.
, т.е. второй дифференциал >0.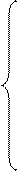

 (3)
(3)
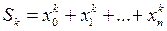
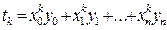 k=(0,1,2)
k=(0,1,2)
 Если m=n, то Qm(x) совпадает с полиномом Лагранжа
Если m=n, то Qm(x) совпадает с полиномом Лагранжа 5 a0 + 11.61 a1 + 32.768 a2 = 11.350
5 a0 + 11.61 a1 + 32.768 a2 = 11.350 ε=Y-Y
ε=Y-Y [f (xi) – Qm(xi)] 2)1/2
[f (xi) – Qm(xi)] 2)1/2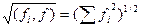
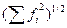 ≈15*10-3 (0.015)
≈15*10-3 (0.015)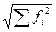 =
= 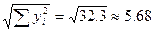
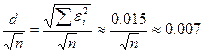


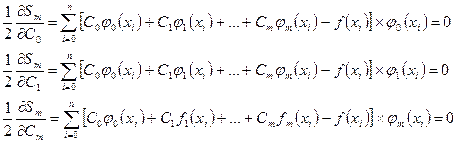 (7)
(7)  C0 (φ0, φ0) + C1 (φ1, φ0) +…+ Cm (φm, φ0) = (f, φ0)
C0 (φ0, φ0) + C1 (φ1, φ0) +…+ Cm (φm, φ0) = (f, φ0)


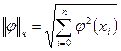 - норма функции φ(х)
- норма функции φ(х)
 определены на этом множестве и из равенства
определены на этом множестве и из равенства  λ0f0 (xі) + λ1f1 (xі) +…+ λmfm (xі) = 0 (і = 1, n)
λ0f0 (xі) + λ1f1 (xі) +…+ λmfm (xі) = 0 (і = 1, n) Следует, что все постоянные λk = 0 (k = 0,m)
Следует, что все постоянные λk = 0 (k = 0,m)



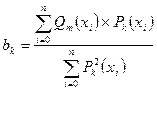 k = 0, 1,…,m (4)
k = 0, 1,…,m (4)

 (i = 0,n)
(i = 0,n)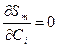
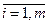 и разрешая полученную систему уравнений, получим:
и разрешая полученную систему уравнений, получим:
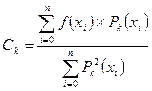 k=
k=  (7)
(7)
 , можно убедиться, что
, можно убедиться, что 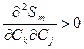 и, следовательно
и, следовательно
 переведем эти точки в t = 0, 1, 2,…, n.
переведем эти точки в t = 0, 1, 2,…, n.
 S = 0 k k k + s n[s]
S = 0 k k k + s n[s] 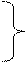
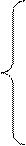 P0, n (t) = 1
P0, n (t) = 1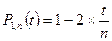 ; (n≥1)
; (n≥1) 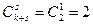 , k=1, s=1
, k=1, s=1 ; (n≥2) (2)
; (n≥2) (2)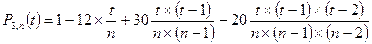 ; (n≥3)
; (n≥3)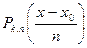 , (k=0,1,…,m; m≤n)
, (k=0,1,…,m; m≤n) равен
равен (3) [n+k+1], [k+1] – обобщенные степени
(3) [n+k+1], [k+1] – обобщенные степени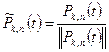 (k=0,1,2,…,m; m≤n) (4)
(k=0,1,2,…,m; m≤n) (4) ;
; 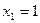 ;
; 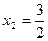 ;
; 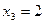 ;
;  ;
; 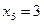
 , переведем точки
, переведем точки 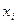 в целочисленные точки t=0,1,2,3,4,5. Теперь в формулах (1) принимаем n=5.
в целочисленные точки t=0,1,2,3,4,5. Теперь в формулах (1) принимаем n=5. Имеем
Имеем 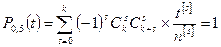 ;
;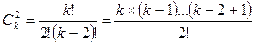




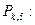 по формуле (3) получаем квадрат нормы, затем вычисляем корень, т.е. норму!
по формуле (3) получаем квадрат нормы, затем вычисляем корень, т.е. норму!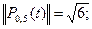

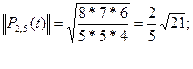
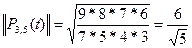
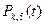 на их нормы и переходим от переменной t к переменной х, получим нормированную систему ортогональных полиномов Чебышева:
на их нормы и переходим от переменной t к переменной х, получим нормированную систему ортогональных полиномов Чебышева:

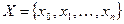 с шагом h, то наилучший аппроксимирующий ее на Х полином степени m будет иметь вид:
с шагом h, то наилучший аппроксимирующий ее на Х полином степени m будет иметь вид:
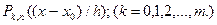
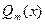 не изменится, если ортогональные полиномы Чебышева
не изменится, если ортогональные полиномы Чебышева  умножить на постоянные множители, отличные от нуля. Т.к.
умножить на постоянные множители, отличные от нуля. Т.к. 
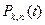 пользуются полиномами
пользуются полиномами  подобраны так, чтобы для целочисленных значений аргумента t значения
подобраны так, чтобы для целочисленных значений аргумента t значения 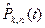 тоже были целочисленными. Имеются (в справочной литературе) таблицы полиномов
тоже были целочисленными. Имеются (в справочной литературе) таблицы полиномов 


