
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок работы с симплекс - таблицейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Первая симплекс-таблица подвергается преобразованию, суть которого заключается в переходе к новому опорному решению. Порядок перехода к следующей таблице такой: 1) просматривается последняя строка таблицы и среди коэффициентов этой строки (исключая g0) выбирается наибольшее по модулю из отрицательных число. Если такового нет, то исходное базисное решение является оптимальным и данная таблица является последней; 2) просматривается столбец таблицы, отвечающий выбранному отрицательному коэффициенту в последней строке, и в этом столбце выбираются положительные коэффициенты. Если таковых нет, то целевая функция неограниченна на области допустимых значений переменных и задача решений не имеет; 3) среди отобранных коэффициентов столбца выбирается тот, для которого абсолютная величина отношения соответствующего свободного члена (находящегося в столбце свободных членов) к этому элементу минимальна. Этот элемент называется разрешающим или генеральным элементом таблицы; 4) в дальнейшем базисная переменная, отвечающая строке разрешающего элемента, должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных; 5) строка разрешающего элемента делится на этот элемент и полученная строка записывается в новую таблицу на то же место. В остальные клетки новой таблицы записывается результат преобразования элементов старой таблицы. Для этого умножают первую из заполненных строк (строку разрешающего элемента) на некоторые числа и складывают ее со строками старой таблицы. Числа эти подбираются так, чтобы в столбце разрешающего элемента получались нули, кроме клетки разрешающего элемента (в которой стоит единица). В результате получают новую симплекс-таблицу, отвечающую новому базисному решению. Теперь следует просмотреть строку целевой функции и повторить все вышеизложенное. Составление новых симплекс-таблиц производится до тех пор, пока все коэффициенты последней строки (кроме стоящего на месте g0) в очередной таблице не станут неотрицательными. После этого считается, что задача решена и по последней симплекс-таблице прочитывается ее ответ. Максимальное значение Zmax целевой функции стоит в первой клетке последней строки на месте g0. Неотрицательные значения новых базисных переменных стоят в клетках столбца свободных членов. Остальные переменные в точке максимума равны нулю.
Пример 2. (Задача об использовании сырья) Для производства четырех видов изделий A1, A2, A3, A4 завод должен использовать три вида сырья I, II, III, запасы которого на планируемый период составляют соответственно 1000, 600 и 150 условных единиц. В приведенной ниже таблице даны технологические коэффициенты, т.е. расход каждого вида сырья на производство единицы каждого изделия и прибыль от реализации единицы изделия каждого вида:
Требуется составить такой план выпуска указанных изделий, чтобы обеспечить максимальную прибыль от их реализации. Обозначим через х1,х2,х3,х4 количество единиц соответствующих изделий: А1, А2, А3, А4. Тогда экономико-математическая модель задачи будет следующая: найти максимум функции F = 6x1 + 2x2 + 2.5x3 + 4x4 ® max при выполнении системы ограничений
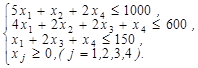 (2.12) (2.12)
Для обращения системы ограничений-неравенств (2.12) в систему уравнений прибавим к левой части каждого неравенства добавочные неотрицательные переменные х5, x6, x7. Эти добавочные переменные в условиях данной задачи имеют конкретное экономическое содержание: объем остатков сырья каждого вида после выполнения плана выпуска продукции. После введения добавочных переменных получим систему уравнений:
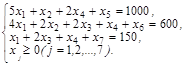 (2.13) (2.13)
Нужно найти такое допустимое базисное решение системы (2.13), которое бы максимизировало целевую функцию F, т.е. необходимо найти оптимальное решение задачи. Для решения задачи симплексным методом прежде всего нужно найти любое базисное решение. Для этого достаточно принять за основные добавочные переменные х5, х6, х7. I шаг. Основные переменные X5, X6, X7. Составляем первую симплекс-таблицу. Находим разрешающий элемент:
Базисное решение (0; 0; 0; 0; 1000; 600; 150).
II шаг. Основные переменные X1, X5, X6. Составляем новую симплекс-таблицу. Снова находим разрешающий элемент:
Базисное решение (150; 0; 0; 0; 250; 0; 0).
III шаг. Основные переменные X1, X2, X5. Составляем новую симплекс-таблицу. Находим разрешающий элемент:
Базисное решение (150; 0; 0; 0; 250; 0; 0).
IV шаг. Основные переменные X2, X4, X5. Переходим к следующей таблице:
Эта таблица является последней, по ней читаем ответ задачи. Оптимальным будет решение (0; 225; 0; 150; 475; 0; 0), при котором Fmax =1050, т.е. для получения наибольшей прибыли, равной 1050 денежных единиц, предприятие должно выпустить 225 единиц продукции вида A2, 150 единиц продукции вида A4 (продукцию вида A1 и A3 в данных условиях производить не выгодно) при этом сырье типа II и III будет использовано полностью, а 475 единиц сырья типа I останутся неизрасходованными.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.100.197 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

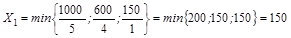 .
.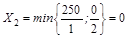 .
.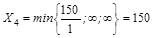 .
.


