
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы двойственностиСодержание книги
Поиск на нашем сайте
Теория двойственности в линейном программировании строится на следующих основных теоремах. Теорема 1. Если задача линейного программирования имеет конечный оптимум, то двойственная к ней также имеет конечный оптимум, и оптимальные значения линейных форм обеих задач совпадают, то есть Fmax = Zmin или Fmin = Zmax . Если линейная форма одной из двойственных задач не ограничена, то условия другой задачи противоречивы. Прежде чем сформулировать теорему 2, установим соответствия между переменными исходной и двойственной задач. При решении симплексным методом исходной задачи для обращения системы неравенств в эквивалентную ей систему уравнений должны быть введены m добавочных неотрицательных переменных (по числу неравенств в системе ограничений): хn+1, хn+2,..., хn+i,..., хn+m, где i=1, 2,..., m означает номер неравенства, в которое была введена добавочная переменная хn+i. Система ограничений двойственной задачи состоит из n неравенств, в которых имеются m переменных. При решении этой задачи симплексным методом необходимо ввести n добавочных неотрицательных переменных: уm+1, ym+2,..., уm+j,..., ym+n , где j = 1, 2,..., n означает номер неравенства системы ограничений двойственной задачи, в которое была введена добавочная переменная уm+j. Установим следующее соответствие между переменными исходной и двойственной задачи:
Иными словами, каждой первоначальной переменной исходной задачи xj (j = 1, 2,..., n) ставится в соответствие добавочная переменная уm+j, введенная в j-е неравенство двойственной задачи, а каждой добавочной переменной xn+i исходной задачи (i = 1, 2,..., m), введенной в i-е неравенство исходной задачи, ставится в соответствие первоначальная переменная yi двойственной задачи. Теорема 2. Компоненты оптимального решения задачи линейного программирования равны абсолютным величинам коэффициентов при соответствующих переменных в выражении линейной формы двойственной ей задачи при достижении ею оптимума. Замечание. Если в одной из задач (прямой или двойственной) нарушается единственность оптимального решения, то оптимальное решение другой задачи будет вырожденным.
Из теорем 1 и 2 следует вывод, что, решив одну из взаимно двойственных задач, то есть найдя ее оптимальное решение и оптимум линейной формы, мы можем записать оптимальное решение и оптимум линейной формы другой задачи. Доказательства теорем не приводятся. Но, решения тех или иных конкретных задач, убеждают в справедливости сформулированных теорем. Рассмотрим еще одну теорему, выводы из которой будут использованы в дальнейшем. Теорема об оценках. Значения переменных уi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi системы ограничений-неравенств прямой задачи на величину Fmax , т. е.
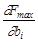 . (2.15) . (2.15)
Эта теорема показывает еще одну связь между переменными прямой и двойственной задач. Поясним это подробнее. Пусть (х1, х2,..., хj,..., xn ) - оптимальное решение прямой задачи, а (у1, у2,..., уi,..., уm) - оптимальное решение двойственной задачи. Оптимальные значения целевых функций F и Z достигаются при подстановке компонент оптимального решения в их первоначальные выражения, т. е.: Fmax = c1x1 +... + cjxj +... + cnxn, Zmin = b1y1 +... + biyi +... + bmym. На основании первой теоремы двойственности (Fmax = Zmin) можно записать c1x1 +... + cjxj +... + cnxn = b1y1 +... + biyi +... + bmym. Отсюда следует, что Fmax = b1у1 +... + biуi +... + bmуm. Поставим вопрос, как изменится величина Fmax, если в исходной задаче увеличить свободный член bi, в i-м ограничении-неравенстве на величину
т.е. мы пришли к формуле (2.16). Учитывая, что функция Fmax линейная, получим
|
|||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.185 (0.006 с.) |

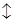
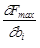 = yi,
= yi,


