
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составление двойственной задачи
Рассмотрим две задачи линейного программирования:
Эти задачи обладают следующими свойствами: 1. В одной задаче ищется максимум линейной формы, а в другой - минимум. 2. Коэффициенты при переменных в линейной форме одной задачи являются свободными членами системы ограничений другой задачи и, наоборот, свободные члены системы ограничений одной задачи являются коэффициентами при переменных в линейной форме другой задачи. 3. В каждой задаче система ограничений задается в виде неравенств, причем все они одного смысла, а именно: в задаче, в которой ищется максимум линейной формы, все неравенства вида « 4. Коэффициенты при переменных систем ограничений описываются матрицами транспонированными относительно друг друга:
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче. 6. Условия неотрицательности переменных сохраняются в обеих задачах. Две задачи линейного программирования, удовлетворяющие указанным выше шести условиям, называются взаимно двойственными задачами. Первоначальную задачу будем называть исходной, или прямой, при этом любую из взаимно двойственных задач можно рассматривать как исходную. Отсюда вытекают следующие правила составления задачи, двойственной исходной (данной): 1. Привести все неравенства системы ограничений исходной задачи к одному виду, а именно: если в исходной задаче ищется максимум линейной формы, то все неравенства системы ограничений привести к виду « 2. Выписать матрицу А коэффициентов при переменных исходной задачи, полученных после преобразований, указанных в пункте 1, и транспонировать ее. 3. Составить систему ограничений двойственной задачи, для чего коэффициентами при переменных взять элементы транспонированной матрицы А’, неравенствам придать противоположный по сравнению с неравенствами пункта 1 смысл, а в качестве свободных членов взять коэффициенты при переменных линейной формы исходной задачи.
4. Составить линейную форму двойственной задачи, взяв коэффициентами при переменных свободные члены системы ограничений исходной задачи, полученные после преобразований пункта 1. 5. Указать, что необходимо найти при решении задачи, а именно: минимум линейной формы, если в исходной задаче ищется максимум, и максимум, если в исходной задаче ищется минимум. 6. Записать условие неотрицательности переменных двойственной задачи.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 78; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.74.54 (0.005 с.) |


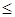 », а в задаче, в которой находится минимум линейной формы,_ противоположного смысла, т. е. «
», а в задаче, в которой находится минимум линейной формы,_ противоположного смысла, т. е. «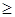 ».
». », а если минимум _ то к виду «
», а если минимум _ то к виду «


