
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая интерпретация оптимизационной задачи линейного программирования в случае двух переменных
Экономико-математическая модель задачи линейного программирования в стандартной форме с двумя переменными имеет вид F = C0 + C1X1 + C2X2 ® max,
x1 ³ 0, x2 ³ 0. Выясним геометрическую интерпретацию совокупности решений одного отдельно взятого неравенства a1x1 + a2x2 £ b. (2.7) Рассмотрим прямую на плоскости с уравнением a1x1 + a2x2 = b. Эта прямая делит плоскость на две полуплоскости, в одной из которых справедливо неравенство (2.6), а в другой – противоположное. Для того чтобы проверить, какая из полуплоскостей состоит из решений неравенства (2.6), следует взять точку из какой-либо полуплоскости и проверить, выполняется ли оно этой точке. Множество решений отдельно взятого линейного неравенства представляет собой полуплоскость. Для системы из нескольких таких неравенств точки, координаты которых удовлетворяют всем неравенствам одновременно, должны находиться во всех соответствующих полуплоскостях, т.е. принадлежать теоретико-множественному пересечению этих полуплоскостей. Множество точек на плоскости, удовлетворяющих системе ограничений, составляет таким образом некоторую выпуклую многоугольную область. Условия неотрицательности переменных X1 ³ 0 и X2 ³ 0 приводят к тому, что эта область находится в первой координатной четверти. Множество точек на плоскости, удовлетворяющих системе ограничений, называют часто допустимым многоугольником. Эта область может быть неограниченной или вовсе пустой. Целевая функция задачи геометрически изображается с помощью прямой уровня, т.е. прямой, на которой Z = C0 + C1X1 + C2X2 принимает постоянное значение. Если С - произвольная константа, то уравнение прямой уровня имеет вид C0 + C1X1 + C2X2 = C. При изменении константы C получаем различные прямые, параллельные друг другу. При увеличении C прямая уровня перемещается в направлении наискорейшего возрастания функции Z, т.е. в направлении ее градиента. Вектор градиента Геометрический метод решения задачи состоит в следующем. Строится допустимый многоугольник и принимается некоторое положение линии уровня целевой функции. Определяется направление перемещения прямой уровня. Точкой минимума F будет точка первого касания линии уровня с допустимым многоугольником. Точкой максимума – точка отрыва линии уровня от допустимого многоугольника. Эти точки чаще всего совпадают с некоторыми вершинами допустимого многоугольника, хотя их может быть и бесчисленное множество, если линия уровня Z параллельна одной из сторон допустимого многоугольника.
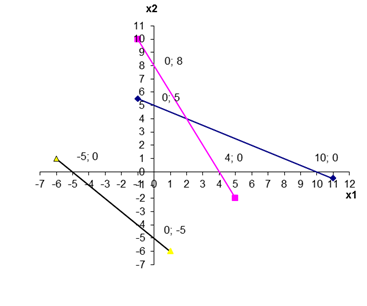
Пример 1. Построим на плоскости множество решений системы неравенств для модели (рис.2.5):
Решим геометрически задачу примера 1 при C1 = 1, C2 = 1 (рис.2.6):
Рис.2.5. Точкой максимума здесь является точка А, координаты которой определяются из следующей системы уравнений: решая которую, получаем точку максимума А (2;4), Zmax = 6. 2.5. Симплекс-метод решения оптимизационных задач Симплексный метод – это вычислительная процедура, основанная на принципе последовательного улучшения решений при переходе от одной базисной точки (базисного решения) к другой. При этом значение целевой функции улучшается. Этот метод является одним из универсальных, применяемым к любой задаче ЛП в канонической форме. Система ограничений здесь – система линейных уравнений, в которой количество неизвестных больше количества уравнений. Базисным решением является одно из допустимых решений, находящихся в вершинах области допустимых значений. Проверяя на оптимальность вершину за вершиной, приходят к искомому оптимуму. На этом принципе основан симплекс-метод. Симплекс – это выпуклый многогранник в n-мерном пространстве с n+1 вершинами, не лежащими в одной гиперплоскости (гиперплоскость делит пространство на два полупространства). Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные: X1,X2,...,Xr. Тогда наша система уравнений может быть записана как
К такому виду можно привести любую совместную систему, например методом Гаусса. Правда, не всегда можно выражать через остальные первые r неизвестных (мы это сделали для определенности записи). Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные - свободными.
Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные X1, X2,..., Xr, то решение {b1,b2,...,br,0,...,0} будет опорным при условии, что b1,b2,...,br ³ 0. Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение Z самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого найденного заранее опорного решения по определенному алгоритму симплекс-метода, мы подсчитываем новое опорное решение, по которому значение целевой функции Z не меньше, чем по старому. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом. Имея систему ограничений, приведенную к общему виду, то есть к системе m линейных уравнений с n переменными (m<n), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то осуществляется переход к другому, обязательно допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении линейная форма если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным. Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляется переход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений. Таким образом, применение симплексного метода распадается на два этапа: 1) нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; 2) нахождение оптимального решения. При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода.
Вычисления по симплекс-методу организуются в виде симплекс-таблиц, которые являются сокращенной записью задачи линейного программирования в канонической форме. Для определенности записи считается, что в качестве базисных переменных можно взять переменные X1,X2,...,Xr и что при этом b1,b2,...,br ³ 0 (соответствующее базисное решение является опорным). Исходная симплекс-таблица выглядит следующим образом:
Примечание. Названия базисных переменных здесь взяты лишь для определенности записи и в реальной таблице могут оказаться другими.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.60 (0.007 с.) |
 (2.6)
(2.6)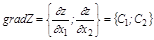 .
. (2.8)
(2.8)



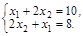
 ,
, (2.9)
(2.9)


