
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экономическая интерпретация двойственной задачиСодержание книги
Поиск на нашем сайте
Составим и решим симплексным методом задачу, двойственную задаче об использовании сырья, сформулированной в 2.4 (см. пример 4). Экономико-математическая модель формулируется так: найти максимум функции F= 6х1 + + 2х2 + 2,5х3 + 4х4, выражающей прибыль предприятия, при следующих ограничениях:
Решение задачи симплексным методом привело к следующему результату: максимальное значение функции F, равное 1050 ден. ед., достигается при оптимальном решении (0, 225, 0, 150, 475, 0, 0). Первые четыре компоненты этого решения дают оптимальный план выпуска продукции, а последние три -остатки сырья видов I, II и III. Рассмотрим эту задачу как исходную и составим двойственную ей. Матрица В условий прямой задачи и матрица В’ - транспонированная матрица В - имеют следующий вид:
В двойственной задаче нужно найти минимум функции Z = 1000y1 + 600y2 +150, при ограничениях Систему ограничений-неравенств двойственной задачи обратим в систему уравнений: Применив теперь алгоритм симплекс-метода, решим поставленную задачу: Zmin= 1050. Оптимальное решение (0; 1; 3; 1; 0; 5.5; 0). Запишем соответствующие переменные прямой и двойственной задач:
Компоненты у1, у2, у3 оптимального решения двойственной задачи оценивают добавочные переменные х5, х6, х7 прямой задачи. Равенство нулю переменной у1 в оптимальном решении свидетельствует о том, что переменная х5 положительна в оптимальном решении прямой задачи, или что подстановка компонент оптимального решения в первое неравенство системы ограничений прямой задачи не обращает его в строгое равенство. Переменные у2, у3 положительны, а соответствующие им переменные прямой задачи х6, х7 равны нулю в оптимальном решении прямой задачи. Подстановка компонент оптимального решения во второе и третье неравенства прямой задачи обращает их в строгие равенства. Экономический смысл этого обстоятельства состоит в том, что сырья вида I у нас имеется с излишком и мы не особенно «дорожим» им, поэтому устанавливаем для него нулевую оценку, а вот сырье видов II и III является дефицитным, оно все целиком расходуется, поэтому мы оцениваем эти виды сырья некоторыми положительными оценками (у2 = 1, у3 = 3). Как оценить единицу сырья каждого вида в зависимости от той прибыли, которую приносит предприятию реализация продукции А1, А2, А3, А4? Подчеркнем, что речь идет не о стоимости сырья при его приобретении предприятием. Нас интересует относительная стоимость сырья с точки зрения получения максимальной прибыли при изменении его запасов. Ясно, что ценность того или иного вида сырья будет определяться величиной роста максимальной прибыли при увеличении, например запаса сырья i-го вида. Cогласно выводу из теоремы об оценках DFmax = yiDbi. В этой формуле уi -компонента оптимального решения двойственной задачи. Здесь особенно ощутимо видна стоимостная сущность переменных двойственной задачи. Они выступают как условные цены единицы i-го вида сырья. Поэтому переменные двойственной задачи часто называют объективно обусловленными оценками. Вернемся к оптимальному плану двойственной задачи. При этом нас будут интересовать только первые три компоненты: у1 = 0, у2 = 1, у3 = 3 этого решения, которые соответствуют добавочным переменным прямой задачи х5, х6, х7, выражающим величины остатков сырья видов I, II, III. Ответим на вопрос: как изменится оптимальный план выпуска продукции, а вместе с ним и максимальная прибыль, если увеличивать запасы сырья каждого вида? Пусть запас сырья вида I увеличился на 100 усл. ед. Пользуясь формулой (5.3), получим DFmax = y1Db1 = 0*100 = 0, т. е. прибыль не увеличится, оптимальное решение не изменится. Последний вывод закономерен, ибо выпуск продукции в условиях прямой задачи лимитируется наличием сырья видов II, III. Увеличим на 100 ед. запас сырья вида II. Тогда DFmax = y2*100 = 1*100 = 100 ден. ед. Решая прямую задачу симплексным методом (рекомендуется сделать самостоятельно) с измененной правой частью второго ограничения-неравенства: 4х1 + 2х2 + 2х3 + х4 (0, 275, 0, 150, 425, 0; 0). Увеличив на 100 усл. ед. запас сырья III, получим DFmax = y3*100 = 3*100 = 300 ден. ед. При этом измененном условии максимальная прибыль равна 1350 усл. ед. при оптимальном плане (0, 175, 0, 250, 325, 0, 0). В справедливости последнего утверждения можно убедиться, решив симплексным методом прямую задачу с измененной правой частью третьего ограничения-неравенства: х1 + 2х3 + х4 £ 250. Примеры решения заданий Пусть необходимо найти оптимальный план производства двух видов продукции Р и R, то есть такой план, при котором целевая функция (общая прибыль) была бы max, а имеющиеся ресурсы использовались бы наилучшим образом. Таблица 2.1 Данные о запасе и нормах расхода ресурсов
Требуется: I. Cформулировать экономико-математическую модель задачи в виде ОЗЛП. II. Привести ОЗЛП к канонической форме. III. Сформулировать экономико-математическую модель задачи двойственной к исходной. IV. Построить многогранник решений (область допустимых решений) и найти оптимальную производственную программу путем перебора его вершин и геометрическим способом. V. Решить задачу с помощью симплекс-таблиц. Решение: I. Оптимизационная модель задачи запишется следующим образом: а) целевая функция
б) ограничения: в) условия неотрицательности переменных х1≥0; х2≥0. II. Приведем ОЗЛП к канонической форме. Для этого введем дополнительные переменные x 3, x 4 и x 5. а) целевая функция
б) ограничения: в) условия неотрицательности переменных III. Сформулируем экономико-математическую модель задачи двойственную к исходной. Матрица В условий прямой задачи и матрица В’ – транспонированная матрица В – имеют следующий вид:
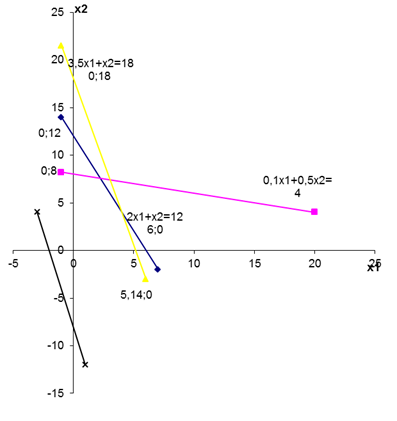
В двойственной задаче нужно найти минимум функции Z = 12y1 + 14y2 +18y3, при ограничениях Систему ограничений-неравенств двойственной задачи обратим в систему уравнений: Компоненты у1, у2, у3 оптимального решения двойственной задачи оценивают добавочные переменные х3, х4, х5 прямой задачи. VI. Построим многогранник решений (область допустимых решений) и найдем оптимальную производственную программу путем перебора его вершин и геометрическим способом. Преобразуем нашу систему ограничений, найдя в каждом из уравнений х2 и отложим их на графике. Любая точка на данном графике с координатами х1, х2 представляет вариант искомого плана. Однако ограничения по ресурсу А сужают область допустимых решений. Ими могут быть все точки, ограниченные осями координат и прямой, так как не может быть израсходовано ресурса больше, чем его на предприятии имеется. Если точки находятся на самой прямой, то ресурс используется полностью. Аналогичные рассуждения можно привести для ресурсов В и С. В результате условиям задачи будет удовлетворять любая точка лежащая в пределах заштрихованного многоугольника. Данный многоугольник называется областью допустимых решений. Определим точки пересечения линий ограничений с осями: 1) 2) 3) Однако нам необходимо найти такую точку, в которой достигался бы max целевой функции. Оптимальную производственную программу можно найти двумя способами: 1) путем перебора его вершин Находим координаты вершин многоугольника ABCDE и подставляя в целевую функцию находим ее значение. А: А (0; 0) Z(A) =4×0+5×0=0 В: В (0; 8) Z(B) = 4×0+5×8=40 С: – это пересечение первого и второго уравнений
С (2,22; 7,55) Z(C) = 4×2,22+5×7,55=8,88+37,77=46,65
D: – это пересечение первого и третьего уравнений
D (4; 4) Z(D)=4×4+5×4=20+25=45 E: (5,14; 0) Z(E) = 4×5,14+5×0=20,56 Находим max значение целевой функции. Оно находится в точке 2) геометрическим способом Целевая функция геометрически изображается с помощью прямой уровня, т.е. прямой на которой Z=C0+C1X1+C2X2 – принимает постоянное значение. Если С – произвольная const, то уравнение прямой имеет вид C0+C1X1+C2X2=С При изменении const С получаем различные прямые, параллельные друг другу. При увеличении С прямая уровня перемещается в направлении наискорейшего возрастания функции Z, т.е. в направлении ее градиента. Вектор градиента Точкой min Z будет точка первого касания линии уровня с допустимым многоугольником. Точкой max – точка отрыва линии уровня от допустимого многоугольника. Эти точки чаще всего совпадают с некоторыми вершинами допустимого многоугольника, хотя их может быть и бесчисленное множество, если линия уровня Z параллельна одной из сторон допустимого многоугольника. Это точка С (2,22; 7,55) Z=46,65 у.д.е. VII. Решим задачу с помощью симплекс-таблиц. Пусть необходимо найти оптимальный план производства двух видов продукции P и R.
F(X)=4X1+5X2→max
F(X)=4X1+5X2→max Построим исходную симплекс-таблицу и найдем начальное базисное решение.
Базисное решение (0; 0; 12; 4; 18). F=0. Находим генеральный столбец и генеральную строку
Базисное решение (0; 8; 4; 0; 10). F=40.
Базисное решение (2,22; 7,56; 0; 0; 2,74). F=46,65. Эта таблица является последней, по ней читаем ответ задачи. Оптимальным будет решение (2,22; 7,56; 0; 0; 2,74), при котором Fmax =46,65, т.е. для получения наибольшей прибыли, равной 46,65 денежных единиц, предприятие должно выпустить 2,22 единиц продукции вида P и 7,56 единиц продукции вида R, при этом ресурсы A и B будут использованы полностью, а 2,74 единиц ресурса С останутся неизрасходованными.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.14 (0.007 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

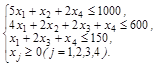
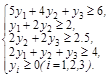
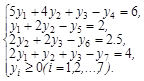
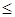 700, получим оптимальное решение
700, получим оптимальное решение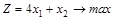
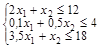
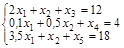
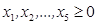 .
.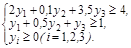
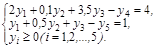
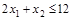 : (0;12) и (6; 0);
: (0;12) и (6; 0); : (0; 8) и (40; 0);
: (0; 8) и (40; 0);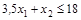 : (0; 18) и (5,14; 0);
: (0; 18) и (5,14; 0);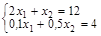 ;
; 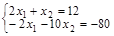 ; -9 x 2=-68 x 2=7,555; x 1=2,222.
; -9 x 2=-68 x 2=7,555; x 1=2,222.

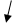






 ; 1,5 x 1=6; x 1=4; x 2=4.
; 1,5 x 1=6; x 1=4; x 2=4.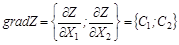
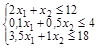
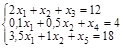
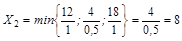 . Генеральный элемент 0,5.
. Генеральный элемент 0,5.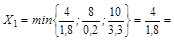 2,22222. Генеральный элемент 1,8.
2,22222. Генеральный элемент 1,8.


